初中数学同步训练必刷题(人教版八年级下册 17.2 勾股定理的逆定理)
试卷更新日期:2023-01-13 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 下列各组数据中,不能作为直角三角形三边长的是( )A、1,2,3 B、3,4,5 C、9,12,15 D、5,12,132. 下列各组数是勾股数的是( )A、5,12,14 B、6,8,12 C、4,5,6 D、7,24,253. 两只蚂蚁在水平地面上从同一地点出发,一只以每分钟12cm的速度朝正东方向爬行,一只以每分钟16cm的速度朝正南方向爬行,10分钟之后两只蚂蚁相距( )A、120cm B、160cm C、200cm D、280cm4. 已知的三条边分别为a,b,c,下列条件不能判断是直角三角形的是( )A、 B、 C、 , , D、5. 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B与灯塔P之间的距离为( )
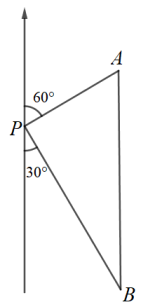 A、60海里 B、45海里 C、20海里 D、30海里6. 如图,在中, , 垂足为D,E为边的中点, , 则( )
A、60海里 B、45海里 C、20海里 D、30海里6. 如图,在中, , 垂足为D,E为边的中点, , 则( ) A、 B、 C、 D、7. 已知一三角形的三边长m,n,p满足 , 则这个三角形的面积为( )A、12 B、60 C、48 D、248. 《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三,乙东行,甲南行十步而斜东北与乙会,问甲、乙行各几何.”大意是说:已知甲、乙两人同时从同一地点出发,甲的速度为7,乙的速度为3,乙一直向东走,甲先向南走10步,后又向东北方向走了一段后与乙相遇,那么相遇时所用时间为多少?若设甲与乙相遇时间为x,则可列方程为( )A、 B、 C、 D、9. 如图,一个圆桶底面直径为8cm,高为12cm,则桶内所能容下的最长木棒的长度为( ).
A、 B、 C、 D、7. 已知一三角形的三边长m,n,p满足 , 则这个三角形的面积为( )A、12 B、60 C、48 D、248. 《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三,乙东行,甲南行十步而斜东北与乙会,问甲、乙行各几何.”大意是说:已知甲、乙两人同时从同一地点出发,甲的速度为7,乙的速度为3,乙一直向东走,甲先向南走10步,后又向东北方向走了一段后与乙相遇,那么相遇时所用时间为多少?若设甲与乙相遇时间为x,则可列方程为( )A、 B、 C、 D、9. 如图,一个圆桶底面直径为8cm,高为12cm,则桶内所能容下的最长木棒的长度为( ).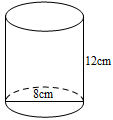 A、8cm B、10cm C、 D、10. “赵爽弦图”巧妙利用面积关系证明勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,若直角三角形较长直角边长为a,较短直角边长为b,且 , 小正方形的面积为3,则大正方形的边长为( )
A、8cm B、10cm C、 D、10. “赵爽弦图”巧妙利用面积关系证明勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,若直角三角形较长直角边长为a,较短直角边长为b,且 , 小正方形的面积为3,则大正方形的边长为( ) A、10 B、7 C、 D、
A、10 B、7 C、 D、二、填空题(每题3分,共30分)
-
11. 木工师傅要做一张长方形的桌面.完成后,量得桌面的长为 , 宽为 , 对角线为130cm,则做出的这个桌面.(填“合格”或“不合格”)12. 如图,每个小正方形的边长为1,点A,B,C是小正方形的顶点,则∠ABC的度数是 .
 13. 如图,圆柱形玻璃杯,高为12cm,底面周长为10cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在玻璃杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为(玻璃杯厚度忽略不计).
13. 如图,圆柱形玻璃杯,高为12cm,底面周长为10cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在玻璃杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为(玻璃杯厚度忽略不计). 14. 如图,四边形ABCD中,AB⊥BC,AB=4,BC=3,AD=12,CD=13,则四边形ABCD的面积是.
14. 如图,四边形ABCD中,AB⊥BC,AB=4,BC=3,AD=12,CD=13,则四边形ABCD的面积是. 15. 一个三角形的三边的比为5:12:13,它的周长为60,则它的面积是 .16. 在中, , , 边上的中线 , 则的长为 .17. 如图,图中的所有四边形都是正方形,三角形是直角三角形,两个小正方形的面积分别是1,2,最大的正方形的面积等于.
15. 一个三角形的三边的比为5:12:13,它的周长为60,则它的面积是 .16. 在中, , , 边上的中线 , 则的长为 .17. 如图,图中的所有四边形都是正方形,三角形是直角三角形,两个小正方形的面积分别是1,2,最大的正方形的面积等于. 18. 如图,这是某种牛奶的长方体包装盒,长、宽、高分别为5cm、4cm、12cm,插吸管处的出口到相邻两边的距离都是1cm,为了设计配套的直吸管,要求插入碰到底面后,外露的吸管长度要在3cm至5cm间(包括3cm与5cm,不计吸管粗细及出口的大小),则设计的吸管总长度L的范围是 .
18. 如图,这是某种牛奶的长方体包装盒,长、宽、高分别为5cm、4cm、12cm,插吸管处的出口到相邻两边的距离都是1cm,为了设计配套的直吸管,要求插入碰到底面后,外露的吸管长度要在3cm至5cm间(包括3cm与5cm,不计吸管粗细及出口的大小),则设计的吸管总长度L的范围是 . 19. 已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积 .
19. 已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积 . 20. 已知a,b,c为三角形的三边,若有(a+c)2=b2+2ac,则这个三角形的形状是三角形.
20. 已知a,b,c为三角形的三边,若有(a+c)2=b2+2ac,则这个三角形的形状是三角形.三、解答题(共6题,共60分)
-
21. 如图,一只小鸟旋停在空中A点,A点到地面的高度米,A点到地面C点(B、C两点处于同一水平面)的距离米.若小鸟竖直下降12米到达D点(D点在线段AB上),求此时小鸟到地面C点的距离.
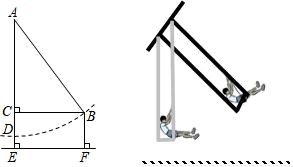
 22. 八(2)班数学兴趣小组来到操场上测量旗杆的高度,小强测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长1米(如图①),小云拉着绳子的下端往后退,当她将绳子拉直时,小晨测得此时小云拉绳子的手到地面的距离为1米,到旗杆的距离为8米(如图②),请你求出旗杆的高度.
22. 八(2)班数学兴趣小组来到操场上测量旗杆的高度,小强测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长1米(如图①),小云拉着绳子的下端往后退,当她将绳子拉直时,小晨测得此时小云拉绳子的手到地面的距离为1米,到旗杆的距离为8米(如图②),请你求出旗杆的高度. 23. 如图,中, , 点E是的中点,求的长.
23. 如图,中, , 点E是的中点,求的长.