初中数学同步训练必刷题(人教版八年级下册 17.1 勾股定理)
试卷更新日期:2023-01-13 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 如图,中, , , 则BC的长为( )
 A、2 B、 C、 D、2. 直角的斜边为5,一条直角边为4,则此三角形的面积是( )A、10 B、20 C、12 D、63. 如图,数轴上的点A表示的数是1,点B表示的数是1,CB⊥AB于点B,且BC=2,以点A为圆心,AC为半径画弧交数轴于点D,则点D表示的数为( )
A、2 B、 C、 D、2. 直角的斜边为5,一条直角边为4,则此三角形的面积是( )A、10 B、20 C、12 D、63. 如图,数轴上的点A表示的数是1,点B表示的数是1,CB⊥AB于点B,且BC=2,以点A为圆心,AC为半径画弧交数轴于点D,则点D表示的数为( ) A、 B、 C、2.8 D、4. 两只蚂蚁在水平地面上从同一地点出发,一只以每分钟12cm的速度朝正东方向爬行,一只以每分钟16cm的速度朝正南方向爬行,10分钟之后两只蚂蚁相距( )A、120cm B、160cm C、200cm D、280cm5. 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B与灯塔P之间的距离为( )
A、 B、 C、2.8 D、4. 两只蚂蚁在水平地面上从同一地点出发,一只以每分钟12cm的速度朝正东方向爬行,一只以每分钟16cm的速度朝正南方向爬行,10分钟之后两只蚂蚁相距( )A、120cm B、160cm C、200cm D、280cm5. 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B与灯塔P之间的距离为( )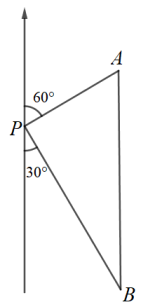 A、60海里 B、45海里 C、20海里 D、30海里6. 如图,在等边中, , 垂足为D,且 , 则的长为( )
A、60海里 B、45海里 C、20海里 D、30海里6. 如图,在等边中, , 垂足为D,且 , 则的长为( ) A、1 B、 C、2 D、7. 如图,△ABC中,∠B=90°,AB=BC=5.现将△ABC沿BC方向平移到△DEF的位置.若平移的距离为3,则CG的长为( )
A、1 B、 C、2 D、7. 如图,△ABC中,∠B=90°,AB=BC=5.现将△ABC沿BC方向平移到△DEF的位置.若平移的距离为3,则CG的长为( ) A、 B、 C、4 D、28. 如图,在正方形网格中,每个小正方形边长都为1,则网格上△ABC中,边长为无理数的边长有( )
A、 B、 C、4 D、28. 如图,在正方形网格中,每个小正方形边长都为1,则网格上△ABC中,边长为无理数的边长有( ) A、0个 B、1个 C、2个 D、3个9. 如图,在四边形ABCD中,∠B=∠D=90°,分别以四边向外做正方形甲、乙、丙、丁,若用S甲、S乙、S丙、S丁来表示它们的面积,那么下列结论正确的是( )
A、0个 B、1个 C、2个 D、3个9. 如图,在四边形ABCD中,∠B=∠D=90°,分别以四边向外做正方形甲、乙、丙、丁,若用S甲、S乙、S丙、S丁来表示它们的面积,那么下列结论正确的是( )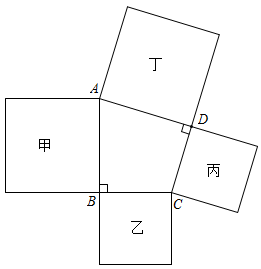 A、S甲= S丁 B、S乙=S丙 C、S甲+S乙=S丙+S丁 D、S甲-S乙=S丙-S丁10. 如图,在Rt△ABC中,∠C=90°,D,E分别为CA,CB的中点,BF平分∠ABC,交DE于点F,若AC=2 , BC=4,则DF的长为( )
A、S甲= S丁 B、S乙=S丙 C、S甲+S乙=S丙+S丁 D、S甲-S乙=S丙-S丁10. 如图,在Rt△ABC中,∠C=90°,D,E分别为CA,CB的中点,BF平分∠ABC,交DE于点F,若AC=2 , BC=4,则DF的长为( ) A、0.5 B、1 C、1.5 D、2
A、0.5 B、1 C、1.5 D、2二、填空题(每题3分,共30分)
-
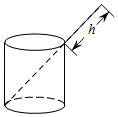
11. 在Rt△ABC中, , 已知AB=15,AC=9,则BC=.12. 如图,一根长16cm的牙刷置于底面直径为6cm、高8cm的圆柱形水杯中,牙刷露在杯子外面的长度为hcm,则h的取值范围是 .
 13. 直角三角形的两直角边长是和3cm,则它的斜边上的高是cm.14. 如图,在中,按以下步骤作图:①分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;②作直线交边于点 . 若 , , , 则的长为 .
13. 直角三角形的两直角边长是和3cm,则它的斜边上的高是cm.14. 如图,在中,按以下步骤作图:①分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;②作直线交边于点 . 若 , , , 则的长为 . 15. 一个三角形两条边长为3和4,当第三条边长为时,此三角形为直角三角形.16. 一根直立于水中的芦节(BD)高出水面(AC)2米,一阵风吹来,芦苇的顶端D恰好到达水面的C处,且C到BD的距离AC=6米,水的深度(AB)为米
15. 一个三角形两条边长为3和4,当第三条边长为时,此三角形为直角三角形.16. 一根直立于水中的芦节(BD)高出水面(AC)2米,一阵风吹来,芦苇的顶端D恰好到达水面的C处,且C到BD的距离AC=6米,水的深度(AB)为米 17. 如图的阴影部分是一个半圆,它的面积是 . (结果保留π)
17. 如图的阴影部分是一个半圆,它的面积是 . (结果保留π) 18. 如图,图1中是第七届国际数学教育大会(ICME-7)会徽图案、它是由一串有公共顶点O的直角三角形(如图2)演化而成的.如果图2中的 , 若代表的面积,代表的面积,以此类推,代表的面则的值为 .
18. 如图,图1中是第七届国际数学教育大会(ICME-7)会徽图案、它是由一串有公共顶点O的直角三角形(如图2)演化而成的.如果图2中的 , 若代表的面积,代表的面积,以此类推,代表的面则的值为 . 19. 某小区两面直立的墙壁之间为安全通道,一架梯子斜靠在左墙DE时,梯子底端A到左墙的距离AE为0.7m,梯子顶端D到地面的距离DE为2.4m,若梯子底端A保持不动,将梯子斜靠在右墙BC上,梯子顶端C到地面的距离CB为2m,则这两面直立墙壁之间的安全通道的宽BE为m.
19. 某小区两面直立的墙壁之间为安全通道,一架梯子斜靠在左墙DE时,梯子底端A到左墙的距离AE为0.7m,梯子顶端D到地面的距离DE为2.4m,若梯子底端A保持不动,将梯子斜靠在右墙BC上,梯子顶端C到地面的距离CB为2m,则这两面直立墙壁之间的安全通道的宽BE为m. 20. 如图,在直线l上摆放着三个正方形,其中正放的两个正方形的顶点M,N分别是斜放正方形相邻两边的中点,三个正方形的面积依次为 , , . 已知 , , 则= .
20. 如图,在直线l上摆放着三个正方形,其中正放的两个正方形的顶点M,N分别是斜放正方形相邻两边的中点,三个正方形的面积依次为 , , . 已知 , , 则= .
三、解答题(共6题,共60分)
-
21. 如图,在一次地震中,一棵垂直于地面且高度为16米的大树被折断,树的顶部落在离树根8米处,即 , 求这棵树在离地面多高处被折断(即求AC的长度)?
 22. 如图,一高层住宅发生火灾,消防车立即赶到距大厦12米(的长)处,升起云梯到火灾窗口,云梯长20米,云梯底部距地面3米(的长),问:发生火灾的住户窗口距离地面有多高(的长)?
22. 如图,一高层住宅发生火灾,消防车立即赶到距大厦12米(的长)处,升起云梯到火灾窗口,云梯长20米,云梯底部距地面3米(的长),问:发生火灾的住户窗口距离地面有多高(的长)?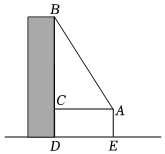 23. 如图,小明在甲岛上的一个观测站A处观测,发现在甲岛的正西方10海里处B点有一艘船向正北方驶去,2小时后,小明再次观察发现该船位于距离甲岛海里的C处,求该船的行驶速度.
23. 如图,小明在甲岛上的一个观测站A处观测,发现在甲岛的正西方10海里处B点有一艘船向正北方驶去,2小时后,小明再次观察发现该船位于距离甲岛海里的C处,求该船的行驶速度. 24. 如图, .
24. 如图, . (1)、尺规作图:作的垂直平分线交于点D,交于点E(不写作法,保留作图痕迹);(2)、在(1)的基础上,连接 , 求的长.
(1)、尺规作图:作的垂直平分线交于点D,交于点E(不写作法,保留作图痕迹);(2)、在(1)的基础上,连接 , 求的长.

