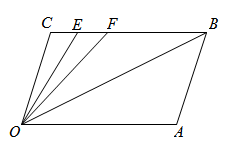
初中数学同步训练必刷题（人教版七年级下册 第五章 相交线与平行线 全章测试卷）
试卷更新日期：2023-01-13 类型：单元试卷
一、单选题（每题3分，共30分）
-
1. 下列各图中，和是对顶角的是（ ）A、
B、
C、
D、
2. 下面四个图案中，能由如图经过平移得到的是（ ）
A、
B、
C、
D、
3. 如图， ， ， 则的度数为（ ）
A、50° B、60° C、140° D、160°4. 如图，AB、CD被EF所截，则∠1与∠2是一对（ ）
A、同位角 B、内错角 C、同旁内角 D、都不是5. 下列说法中正确的个数有（ ）①经过一点有且只有一条直线与已知直线垂直；②经过直线外一点，有且只有一条直线与已知直线平行；③连接直线外一点与直线上各点的所有线段中，垂线段最短；④两条直线相交，对顶角相等.
A、1个 B、2个 C、3个 D、4个6. 如图，点E在BC的延长线上，下列条件中能判定CDAB的是（）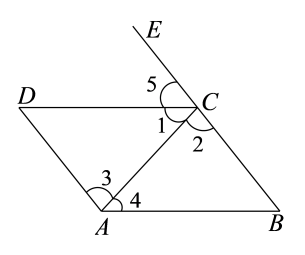
①∠1=∠4②∠2=∠3③∠5=∠B④∠DCB+∠B=180°
A、①②③④ B、①②③ C、①③④ D、①②7. 如图，直线a∥b，直线c与直线a，b分别交于点A，B，AD⊥b于点D，若∠1=57°，则∠2的度数为（ ）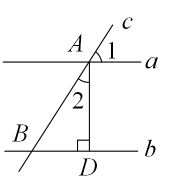
A、30° B、32° C、33° D、40°8. 在同一平面内，下列命题是假命题的是（ ）A、过直线外一点有且只有一条直线与已知直线平行 B、连接直线外一点与直线上各点的所有线段中，垂线段最短 C、在同一平面内，过一点有且只有一条直线与已知直线垂直 D、平面内三条直线两两相交，则它们只有一个交点9. 如图：已知 ， 度， 度，则 等于（ ）度．
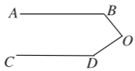A、50 B、60 C、80 D、9010. 如果两个角的两边分别平行，其中一个角是50°，则另一个角是（ ）A、50° B、130° C、50°或130° D、40°二、填空题（每题3分，共30分）
-
11. 如图，O是直线AB上一点，∠COB=30°，则∠1=.
12. 如图，小华同学的家在点P处，他想尽快到公路边，所以选择沿线段PC去公路边，那么他的这一选择体现的数学基本事实是 ．
13. 如图，和∠A是同位角的有 ．
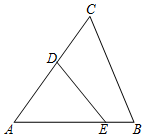14. 若直线 a//直线 b，直线 b//直线 c，则直线 a 和直线 c 的位置关系是 ．15. 用两个相同的三角板如图所示摆放，直线a∥b，画图依据是： ．
16. 如图， ， 直线EF分别交AB、CD于E、F，EG平分∠BEF，若∠1=72°，则∠2= ．
17. 下列三个命题：①两个角的和等于平角时，这两个角互为邻补角；②两直线平行，内错角相等；③同旁内角互补，它们是真命题的是 ． （填序号）18. 如图，三角形ABC向右平移得到三角形DEF，若BC＝6cm，EC＝2cm，则CF＝ ．
19. 如图，直线AB//CD，点M、N分别在直线AB、CD上，点E为直线AB与CD之间的一点，连接ME、NE，且∠MEN=80°，∠AME的角平分线与∠CNE的角平分线交于点F，则∠MFN的度数为 ．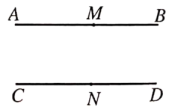
20. 如图，已知 ， 、 为 上的两点， 、 为 上的两点，延长 于点 ， 平分 ，点 在直线 上，且 平分 ，若 ．则下列结论：① ；② ；③ ；④设 ， ；⑤ 的度数为50°．其中正确结论为 ． （填序号）
三、解答题（共6题，共60分）
-
21. 如图， ， ． 求证： ．
证明：∵（ ），（ ），
∴（ ），∴（ ），
∴（ ），
∵（ ），
∴（ ），
∴（ ）．
22. 已知：如图，CD⊥AB，FG⊥AB，垂足分别为D，G，点E在AC上，且∠1=∠2，那么DE与BC平行吗？为什么？
23. 如图：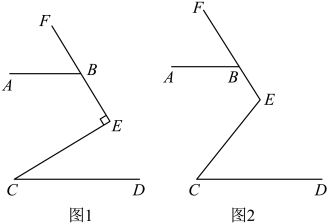
(1)、如图1，∠CEF=90°，点B在射线EF上，若∠ABF=50°，∠C=40° ，试判断AB、CD的位置关系，并说明理由；(2)、如图2，∠CEF=120° ，点B在射线EF上，且 ． 则∠ABE与∠C的数量关系为：
