陕西省宝鸡市教育联盟2022-2023学年高一上学期数学期末试卷
试卷更新日期:2023-01-13 类型:期末考试
一、单选题
-
1. ( )A、 B、 C、 D、2. 已知集合 , , 则( )A、 B、 C、 D、3. 若命题“ , 使得”是假命题,则实数的取值范围是( )A、 B、 C、 D、4. 已知 , , , 则a,b,c的大小关系为( )A、 B、 C、 D、5. 函数的图象大致为( )A、
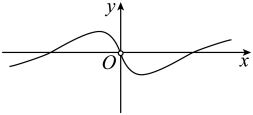
B、
B、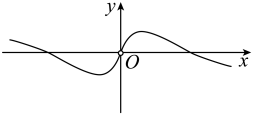
C、
C、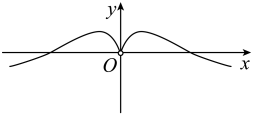
D、
D、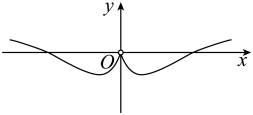
6. 函数的零点所在的区间是( )A、 B、 C、 D、7. 若函数的图象向右平移个单位长度后,得到的图象,则下列关于函数的说法中,正确的是A、函数的图象关于直线对称 B、函数的图象关于点对称 C、函数的单调递增区间为 , D、函数是偶函数8. 神舟十二号载人飞船搭载3名宇航员进入太空,在中国空间站完成了为期三个月的太空驻留任务,期间进行了很多空间实验,目前已经顺利返回地球.在太空中水资源有限,要通过回收水的方法制造可用水.回收水是将宇航员的尿液、汗液和太空中的水收集起来经过特殊的净水器处理成饮用水,循环使用.净化水的过程中,每增加一次过滤可减少水中杂质20%,要使水中杂质减少到原来的5%以下,则至少需要过滤的次数为( )(参考数据)A、10 B、12 C、14 D、16
6. 函数的零点所在的区间是( )A、 B、 C、 D、7. 若函数的图象向右平移个单位长度后,得到的图象,则下列关于函数的说法中,正确的是A、函数的图象关于直线对称 B、函数的图象关于点对称 C、函数的单调递增区间为 , D、函数是偶函数8. 神舟十二号载人飞船搭载3名宇航员进入太空,在中国空间站完成了为期三个月的太空驻留任务,期间进行了很多空间实验,目前已经顺利返回地球.在太空中水资源有限,要通过回收水的方法制造可用水.回收水是将宇航员的尿液、汗液和太空中的水收集起来经过特殊的净水器处理成饮用水,循环使用.净化水的过程中,每增加一次过滤可减少水中杂质20%,要使水中杂质减少到原来的5%以下,则至少需要过滤的次数为( )(参考数据)A、10 B、12 C、14 D、16二、多选题
-
9. 已知函数在区间上单调,则实数m的值可以是( )A、0 B、8 C、16 D、2010. 下列既是存在量词命题又是真命题的是( )A、 , B、至少有个 , 使能同时被和整除 C、 , D、每个平行四边形都是中心对称图形11. 是定义在上的偶函数,当时, , 则下列说法中错误的是( )A、的单调递增区间为 B、 C、的最大值为4 D、的解集为12. 已知 , 为正实数,且 , , , 则( )A、的最大值为 B、的最小值为 C、的最小值为 D、的最小值为
三、填空题
-
13. 已知扇形的半径为2,面积是2,则扇形的圆心角(正角)的弧度数是.14. 设实数满足 , 函数的最小值为.15. 已知函数 , 则的对称中心为.16. 已知关于的方程的两根分别在区间 , 内,则实数的取值范围为 .
四、解答题
-
17. 计算下列各式的值:(1)、;(2)、.18. 已知集合 ,(1)、当时,求 ,(2)、若“”是“”成立的充分不必要条件,求实数的取值范围.19. 已知函数的图象的一条对称轴是.(1)、求的单调减区间;(2)、求的最小值,并求出此时的取值集合.