山西省大同市杨高县2021-2022学年七年级下学期第二次学情监测（月考）数学试题

试卷更新日期：2023-01-13 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列方程组中，是二元一次方程组的是（）

A、 ${\begin{array}{l} x + y = 2 \\ y - z = 8 \end{array}$ B、 ${\begin{array}{l} x y - y = 4 \\ y = 3 \end{array}$ C、 ${\begin{array}{l} x + y = 1 \\ x - y = 3 \end{array}$ D、 ${\begin{array}{l} x + y = 1 \\ \frac{1}{x} - y = 1 \end{array}$

查看试题解析
2. 在如图的象棋盘上，建立适当的平面直角坐标系，使“帅”位于点 $(- 2 ， - 1)$ ， “炮”位于点 $(- 1 ， 1)$ 上，则“兵”位于点（）

A、 $(- 3 ， 3)$ B、 $(- 4 ， 2)$ C、 $(- 3 ， 2)$ D、 $(2 ， - 1)$

查看试题解析
3. 用代入法解方程组 ${\begin{cases} y = 1 - x \\ x - 2 y = 4 \end{cases}$ 时，代入正确的是（）

A、x－2－x＝4 B、x－2－2x＝4 C、x－2＋2x＝4 D、x－2＋x＝4

查看试题解析
4. 解方程组 ${\begin{array}{l} 3 x + 2 y = 5 ① \\ - 2 x + 2 y = - 6 ② \end{array}$ 用①－②，得（）

A、 $x = - 1$ B、 $x = 11$ C、 $5 x = 11$ D、 $5 x = - 1$

查看试题解析
5. 估计2+ $\sqrt{19}$ 的值是（）

A、在5和6之间 B、在6和7之间 C、在7和8之间 D、在8和9之间

查看试题解析
6. 若 $| 3 x - 2 y - 1 | + \sqrt{x + y - 2} = 0$ ，则x，y的值为（）

A、 ${\begin{matrix} x = 1 \\ y = 4 \end{matrix}$ B、 ${\begin{matrix} x = 2 \\ y = 0 \end{matrix}$ C、 ${\begin{matrix} x = 0 \\ y = 2 \end{matrix}$ D、 ${\begin{matrix} x = 1 \\ y = 1 \end{matrix}$

查看试题解析
7. 我国古代数学著作《孙子算经》中有一道题：“今有木，不知长短，引绳度之，余绳四尺五，屈绳量之，不足一尺，问木长几何？”大致意思是：“用根绳子去量一根木条，绳子剩余4.5尺，将绳子对折再量木条，木条剩余1尺，问木条长多少尺？”设绳子长为 $x$ 尺，木条长为 $y$ 尺，则根据题意所列方程组正确的是（）

A、 ${\begin{array}{l} x - y = 4.5 \\ \frac{1}{2} x - y = 1 \end{array}$ B、 ${\begin{array}{l} x - y = 4.5 \\ y - \frac{1}{2} x = 1 \end{array}$ C、 ${\begin{array}{l} x - y = 4.5 \\ x - \frac{1}{2} y = 1 \end{array}$ D、 ${\begin{array}{l} x - y = 4.5 \\ \frac{1}{2} y - x = 1 \end{array}$

查看试题解析
8. 用白铁皮做罐头盒，每张铁皮可制盒身25个，或制盒底40个，一个盒身与两个盒底配成一套罐头盒．现有45张白铁皮，设用 $x$ 张制盒身， $y$ 张制盒底，恰好配套．则下列方程组中正确的是（）

A、 ${\begin{array}{l} x + y = 45 \\ y = 2 x \end{array}$ B、 ${\begin{array}{l} x + y = 45 \\ 25 x = 2 \times 40 y \end{array}$ C、 ${\begin{array}{l} x + y = 45 \\ 25 x = \frac{40 y}{2} \end{array}$ D、 ${\begin{array}{l} x + y = 45 \\ \frac{2 x}{25} = \frac{y}{40} \end{array}$

查看试题解析
9. 如图，将正方形 $A B C D$ 的一角折叠，折痕为 $A E$ ，点 $B$ 落在点 $B ′$ 处， $∠ B ′ A D$ 比 $∠ B A E$ 大 $48 °$ .设 $∠ B A E$ 和 $∠ B ′ A D$ 的度数分别为 $x °$ 和 $y °$ ，那么 $x$ 和 $y$ 满足的方程组是（）

A、 ${\begin{array}{l} y - x = 48 \\ y + x = 90 \end{array}$ B、 ${\begin{array}{l} y - x = 48 \\ y = 2 x \end{array}$ C、 ${\begin{array}{l} x - y = 48 \\ y + 2 x = 90 \end{array}$ D、 ${\begin{array}{l} y - x = 48 \\ y + 2 x = 90 \end{array}$

查看试题解析
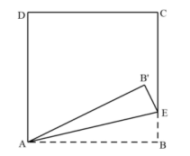10. 把一根长7m的钢管截成2m长和1m长两种规格的钢管，如果不造成浪费，那么共有种不同的截法（　　）

A、6 B、5 C、4 D、3

查看试题解析

二、填空题

11. 已知 $x - 2 y - 1 = 0$ ，用含 $x$ 的代数式表示 $y$ ，则y=

查看试题解析
12. －8的立方根是. $\sqrt{(- 4)^{2}}$ ＝. $\sqrt{16}$ 的算术平方根是.

查看试题解析
13. 在平面直角坐标系中，已知点 $M (m - 1, 2 m + 3)$ 在 $x$ 轴上，则 $m =$ .

查看试题解析
14. 如图，桌子上放了一个台灯，台灯主杆AB垂直于桌面调节杆BC连接主杆和灯罩，灯罩CD平行于桌面，则∠ABC+∠BCD=度．

查看试题解析
15. 甲、乙二人分别从相距 $20 k m$ 的A，B两地出发，相向而行．右上图是小华绘制的甲、乙二人两次运动的情形，设甲的速度是 $x k m / h$ ，乙的速度是 $y k m / h$ ，根据题意可列的方程组是．

查看试题解析

三、解答题

16.

(1)、计算： ${(- 1)}^{2018} + | 1 - \sqrt{2} | - \sqrt[3]{8}$ ．

(2)、解方程组： ${\begin{array}{l} 5 x - 2 y = 12 \\ 3 x - 4 y = 10 \end{array}$ ．

查看试题解析
17. 如图，三角形 $A^{'} B^{'} C^{'}$ 是由三角形 $A B C$ 经过某种平移得到的，点A与点 $A^{'}$ ，点B与点 $B^{'}$ ，点C与点 $C^{'}$ 分别对应，观察点与点坐标之间的关系，解答下列问题.

(1)、直接写出点A和点 $A^{'}$ 的坐标，并说明三角形 $A^{'} B^{'} C^{'}$ 是由三角形 $A B C$ 经过怎样的平移得到的.

(2)、若点 $M (a + 2 ， 4 - b)$ 是点 $N (2 a - 3 ， 2 b - 5)$ 通过（1）中的平移变换得到的，求 ${(b - a)}^{2}$ 的值.

查看试题解析
18. 已知 ${\begin{array}{l} x = 3 \\ y = 1 \end{array}$ 、 ${\begin{array}{l} x = - 1 \\ y = - \frac{5}{3} \end{array}$ 是关于 $x$ 、 $y$ 的二元一次方程 $a x + b y = 3$ 的两组解．

(1)、求 $a$ ， $b$ 的值；

(2)、当 $x = 5$ ， $y = - 1$ 时，求代数式 $a x + b y$ 的值．

查看试题解析
19. 为了鼓励市民节约用电，某市对居民用电实行阶梯收费（总电费＝第一阶梯电费＋第二阶梯电费），规定：用电量不超过200度按第一阶梯电价收费，超过200度的部分按第二阶梯电价收费．以下是张磊家2014年3月和4月所交电费的收据，问该市规定的第一阶梯电价和第二阶梯电价分别为每度多少元？
代收电费收据
电表号
1205
电表号
1205
户名
张磊
户名
张磊
月份
3月
月份
4月
用电量
220度
用电量
265度
金额
112元
金额
139元

查看试题解析
20. 如图，点 $D$ 、 $E$ 分别在 $△ A B C$ 的边 $A B$ 、 $A C$ 上，连接 $D C$ 、 $D E$ ，在 $C D$ 上取一点 $F$ ，连接 $E F$ ，若 $∠ 1 + ∠ 2 = 180 °$ ， $∠ 3 = ∠ B$ ，求证： $D E ∥ B C$ ．

查看试题解析
21. 商店里把塑料凳整齐地叠放在一起，据图中提供的信息，当有10张塑料凳整齐地叠放在一起时，总高度是多少厘米？

查看试题解析
22. 先阅读下列材料，再完成任务：
有些关于方程组的问题，欲求的结果不是每一个未知数的值，而是关于未知数的代数式的值，如以下问题：
已知实数 $x$ 、 $y$ 满足 $3 x - y = 5$ ①， $2 x + 3 y = 7$ ②，求 $x - 4 y$ 和 $7 x + 5 y$ 的值．
本题常规思路是将①②两式联立组成方程组，解得 $x$ 、 $y$ 的值再代入欲求值的代数式得到答案，常规思路运算量比较大．其实，仔细观察两个方程未知数的系数之间的关系，本题还可以通过适当变形整体求得代数式的值，如由①－②可得 $x - 4 y = - 2$ ，由①＋②×2可得 $7 x + 5 y = 19$ ．
这样的解题思想就是通常所说的“整体思想”．
解决问题：

(1)、已知二元一次方程组 ${\begin{array}{l} 2 x + y = 7 \\ x + 2 y = 8 \end{array}$ ，则 $x - y =$ ， $x + y =$ ；

(2)、某班级组织活动购买小奖品，买20支铅笔、3块橡皮、2本日记本共需32元，买39支铅笔、5块橡皮、3本日记本共需58元，则购买1支铅笔、1块橡皮、1本日记本共需多少元？

查看试题解析
23. 综合与实践
问题情境
为了满足农民的消费需求，国家运用财政和贸易政策为工商企业研发和制造符合农民需求的特色产品进行补助．某电器公司计划用甲、乙两种汽车运送190台家电到农村销售，已知甲种汽车每辆可运送家电20台，乙种汽车每辆可运送家电30台，且规定每辆汽车按规定满载，一共用了8辆汽车运送．
针对这个问题，在《二元一次方程组》这一章的学习时，同学们根据下列条件探索还能求出那些量．

(1)、小宇同学根据题意列出了一个尚不完整的方程组 ${\begin{array}{l} x + y = ? \\ 20 x + 30 y = * \end{array}$ ，请写出小宇所列方程组中未知数 $x$ ， $y$ 表示的意义： $x$ 表示， $y$ 表示，该方程组中“？”处的数应是， “*”处的数应是；

(2)、小琼同学的思路是设甲种汽车运送 $m$ 台家电，乙种汽车运送 $n$ 台家电．下面请你按照小琼的思路列出方程组，并求甲种汽车的数量．

查看试题解析

电表号	1205	电表号	1205
户名	张磊	户名	张磊
月份	3月	月份	4月
用电量	220度	用电量	265度
金额	112元	金额	139元