山西省孝义市2021-2022学年七年级下学期阶段性练习(一)数学试题
试卷更新日期:2023-01-13 类型:月考试卷
一、单选题
-
1. 2022年2月4日,第二十四届冬季奥林匹克运动会在北京隆重开幕.此次冬奥会会徽是以汉字“冬”为灵感来源设计的.在下面的四个图中,能由下图经过平移得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 如图,下列条件中,不能判断直线a//b的是( )
2. 如图,下列条件中,不能判断直线a//b的是( ) A、∠1=∠3 B、∠2=∠3 C、∠4=∠5 D、∠2+∠4=180°3. 下列说法正确的是( )A、25的平方根是5 B、是的一个平方根 C、负数没有立方根 D、立方根等于它本身的数是0,14. 已知 , 若 , 则x的值约为( )A、326000 B、3260 C、3.26 D、0.3265. 如图,// , 一副三角尺按如图所示放置,∠AEG=20°,则∠HFD的度数为( )
A、∠1=∠3 B、∠2=∠3 C、∠4=∠5 D、∠2+∠4=180°3. 下列说法正确的是( )A、25的平方根是5 B、是的一个平方根 C、负数没有立方根 D、立方根等于它本身的数是0,14. 已知 , 若 , 则x的值约为( )A、326000 B、3260 C、3.26 D、0.3265. 如图,// , 一副三角尺按如图所示放置,∠AEG=20°,则∠HFD的度数为( )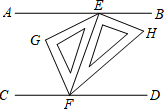 A、20° B、70° C、45° D、35°6. 一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向上行驶,那么两次拐弯的方向可能是( )A、第一次右转40°,第二次右转50° B、第一次右转40°,第二次左转50° C、第一次右转40°,第二次左转140° D、第一次右转40°,第二次左转40°7. 的算术平方根是( )A、3 B、 C、 D、98. 遇到一个新问题时,常常把它转化为已知的(或已解决的)问题.比如,在学习“平行线的判定”一节内容时,我们先得到“同位角相等,两直线平行”,然后利用“同位角相等,两直线平行”得到“内错角相等,两直线平行”.在这一过程中,渗透的数学思想是( )A、类比思想 B、数形结合思想 C、转化思想 D、从一般到特殊思想9. 如图,在一块长为30m,宽为20m的长方形草地上,有一条弯曲的小路,小路的左边线向右平移2m就是它的右边线,则这块草地的绿地面积是( )
A、20° B、70° C、45° D、35°6. 一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向上行驶,那么两次拐弯的方向可能是( )A、第一次右转40°,第二次右转50° B、第一次右转40°,第二次左转50° C、第一次右转40°,第二次左转140° D、第一次右转40°,第二次左转40°7. 的算术平方根是( )A、3 B、 C、 D、98. 遇到一个新问题时,常常把它转化为已知的(或已解决的)问题.比如,在学习“平行线的判定”一节内容时,我们先得到“同位角相等,两直线平行”,然后利用“同位角相等,两直线平行”得到“内错角相等,两直线平行”.在这一过程中,渗透的数学思想是( )A、类比思想 B、数形结合思想 C、转化思想 D、从一般到特殊思想9. 如图,在一块长为30m,宽为20m的长方形草地上,有一条弯曲的小路,小路的左边线向右平移2m就是它的右边线,则这块草地的绿地面积是( )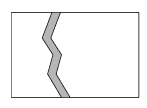 A、 B、 C、 D、10. 公元前6世纪,古希腊的( )学派有一种观点,即“万物皆数”,一切量都可以用整数或整数的比(分数)表示.后来,当这一学派中的希帕索斯发现边长为1的正方形的对角线的长度不能用整数或整数的比表示,即不是有理数时,引发了第一次数学危机.随着人们认识的不断深入,这一学派逐渐承认不是有理数,并给出了证明A、毕达哥拉斯 B、欧几里得 C、丢番图 D、阿基米德
A、 B、 C、 D、10. 公元前6世纪,古希腊的( )学派有一种观点,即“万物皆数”,一切量都可以用整数或整数的比(分数)表示.后来,当这一学派中的希帕索斯发现边长为1的正方形的对角线的长度不能用整数或整数的比表示,即不是有理数时,引发了第一次数学危机.随着人们认识的不断深入,这一学派逐渐承认不是有理数,并给出了证明A、毕达哥拉斯 B、欧几里得 C、丢番图 D、阿基米德二、填空题
-
11. 写出一个大于2且小于4的无理数: .12. 为了丰富学生的课余生活,进一步增强学生的身体素质,某校决定召开春季运动会.各班积极准备,选拔优秀队员参加比赛.如图,是该校七年级1班王明同学在跳远选拔比赛中最好的一跳,甲、乙、丙三名同学分别测得PA=5.55米,PB=5.42米,MA=5.63米,那么他的跳远成绩应该为米.
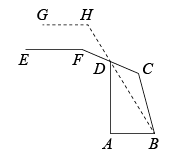
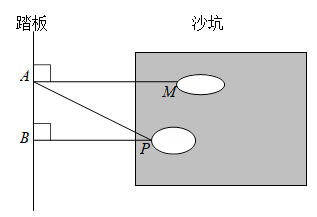 13. 将“平行于同一条直线的两条直线平行”改写成“如果……那么……”的形式为.14. 如图是放置在水平操场上的篮球架及其侧面示意图,已知篮球架的横梁EF始终平行于底座AB,主柱AD垂直于地面.调整前,横梁EF与上拉杆CF形成的∠F=140°,当∠CDB=25°时,点H,D,B在同一条直线上,此时∠H的度数是 .
13. 将“平行于同一条直线的两条直线平行”改写成“如果……那么……”的形式为.14. 如图是放置在水平操场上的篮球架及其侧面示意图,已知篮球架的横梁EF始终平行于底座AB,主柱AD垂直于地面.调整前,横梁EF与上拉杆CF形成的∠F=140°,当∠CDB=25°时,点H,D,B在同一条直线上,此时∠H的度数是 .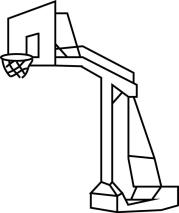
 15. 据说,我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:一个数是59319,希望求它的立方根.华罗庚脱口而出:39.邻座的乘客十分惊奇,忙问计算的奥秘.华罗庚给出了如下方法:(1)由 , , 确定是两位数;(2)由59319个位上的数是9,确定个位上的数是9;(3)划去59319后面的三位319得到59,而 , , 由此确定十位上的数是3.请你类比上述过程,确定21952的立方根是 .
15. 据说,我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:一个数是59319,希望求它的立方根.华罗庚脱口而出:39.邻座的乘客十分惊奇,忙问计算的奥秘.华罗庚给出了如下方法:(1)由 , , 确定是两位数;(2)由59319个位上的数是9,确定个位上的数是9;(3)划去59319后面的三位319得到59,而 , , 由此确定十位上的数是3.请你类比上述过程,确定21952的立方根是 .三、解答题
-
16.(1)、计算:(2)、计算:(3)、解方程:17. 【教材回顾】如下是人教版七年级下册教材第6页,关于同旁内角的定义.
【类比探究】
图中∠3和∠6也都在直线AB、CD之间,但它们在直线EF的同一旁(左侧),具有这种位置关系的一对角叫做同旁内角.
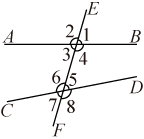
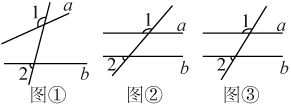 (1)、如图①,具有∠1与∠2这种位置关系的两个角叫做同旁外角,请在图中再找出一对同旁外角,分别用∠3,∠4在图中标记出来;(2)、如图②,直线// , 当∠1=155°时,∠2的度数是 .(3)、如图③,已知∠1+∠2=180°时,试说明直线// , 并用文字叙述由此你能得出什么结论.18. 如图,在正方形网格中,每个小正方形的边长均为1个单位长度,三角形ABC的三个顶点都在网格顶点处,现将三角形ABC平移得到三角形DEF,使点A的对应点为点D,点B的对应点为点E.
(1)、如图①,具有∠1与∠2这种位置关系的两个角叫做同旁外角,请在图中再找出一对同旁外角,分别用∠3,∠4在图中标记出来;(2)、如图②,直线// , 当∠1=155°时,∠2的度数是 .(3)、如图③,已知∠1+∠2=180°时,试说明直线// , 并用文字叙述由此你能得出什么结论.18. 如图,在正方形网格中,每个小正方形的边长均为1个单位长度,三角形ABC的三个顶点都在网格顶点处,现将三角形ABC平移得到三角形DEF,使点A的对应点为点D,点B的对应点为点E.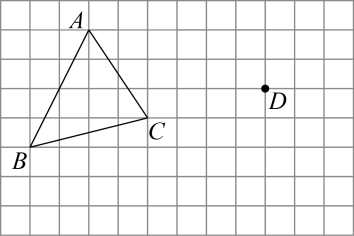 (1)、请画出平移后的三角形DEF;(2)、求三角形DEF的面积;(3)、若连接AD、CF,则这两条线段之间的关系是 .19. 补全下面的解答过程.如图,ABCD,点E,F在直线CD下方,连接BE,DE,BF,DF.BF与CD交于点G.已知BE平分∠ABF,DE平分∠CDF,∠F=∠BGD,探究∠E与∠CDF的数量关系.
(1)、请画出平移后的三角形DEF;(2)、求三角形DEF的面积;(3)、若连接AD、CF,则这两条线段之间的关系是 .19. 补全下面的解答过程.如图,ABCD,点E,F在直线CD下方,连接BE,DE,BF,DF.BF与CD交于点G.已知BE平分∠ABF,DE平分∠CDF,∠F=∠BGD,探究∠E与∠CDF的数量关系.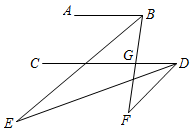
解:∵ABCD,
∴∠ABF=∠ ▲ ( ).
∵BE平分∠ABF,
∴ , ( ).
∵ ,
∴∠EBF=∠ ▲ ( ).
∴BEDF( ).
∴∠ ▲ =∠EDF( ).
∵DE平分∠CDF,
∴∠CDF=2∠EDF( ).
∴ ▲ .
20. 阅读与思考请阅读下面材料,并完成相应的任务.
在学习完实数的相关运算之后,某数学兴趣小组提出了一个有趣的问题:两个数的积的算术平方根与这两个数的算术平方根的积存在什么关系?小聪和小明分别用自己的方法进行了验证:
小聪: , ,
所以 .
小明: , .
这就说明和都是的算术平方根,而的算术平方根只有一个,
所以 .
任务:
(1)、猜想:当 , 时,和之间存在怎样的关系?并仿照小聪或小明的方法举出一个例子进行说明;(2)、运用以上结论,计算:①;②;(3)、解决实际问题:已知一个长方形的长为 , 宽为 , 求这个长方形的面积.21. 潜望镜是指从海面下伸出海面或从低洼坑道伸出地面,用以窥探海面或地面上活动的装置.其构造与普通地上望远镜相同,另加两个反射镜使从摄入潜望镜的光线经两次反射而折向眼中.潜望镜常用于潜水艇、坑道和坦克内用以观察敌情.如图,进入潜望镜的光线和离开潜望镜的光线是平行的,光线经过镜子反射时,∠1=∠2,∠3=∠4,请猜想潜望镜中两面镜子的位置关系,并说明理由.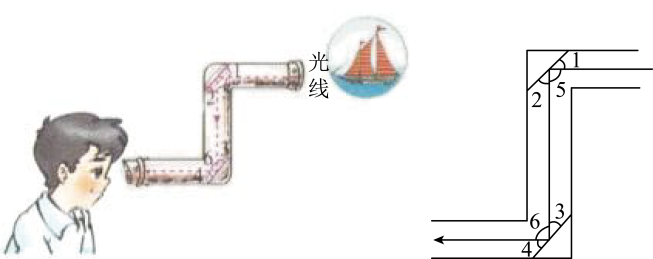 22. 在数学活动课上,老师出示了如下问题:如图1,已知直线ABCD,将三角形纸片EFG的顶点E放到直线AB上,点F落在直线AB与CD所夹区域的内部,FG与CD交于点H,试探究∠EFH,∠BEF,∠DHF之间的数量关系.“兴趣小组”给了如下探究思路:过点F作FTAB.因为ABCD,∴FTCD.∴∠BEF=∠TFE,……
22. 在数学活动课上,老师出示了如下问题:如图1,已知直线ABCD,将三角形纸片EFG的顶点E放到直线AB上,点F落在直线AB与CD所夹区域的内部,FG与CD交于点H,试探究∠EFH,∠BEF,∠DHF之间的数量关系.“兴趣小组”给了如下探究思路:过点F作FTAB.因为ABCD,∴FTCD.∴∠BEF=∠TFE,……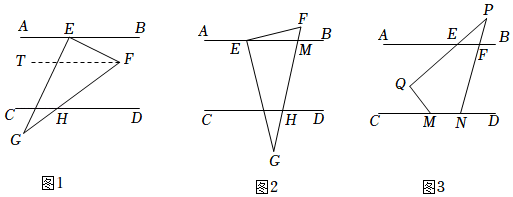 (1)、数学思考:请你根据“兴趣小组”的探究思路,直接写出∠EFH,∠BEF,∠DHF之间的数量关系: .(2)、问题解决:“智慧小组”把老师提出的问题作了如下变式:将三角形纸片EFG如图2所示放置,使得点F落在AB,CD区域的外部,FG与AB,CD分别交于点M,H.试探究∠EFH,∠BEF,∠DHF之间的数量关系.请你类比“兴趣小组”的探究思路,解决智慧小组提出的问题.(3)、结论运用:如图3,直线ABCD,∠PND=75°,∠EPF=35°,∠PQM=95°.请你运用问题(1),(2)得到的结论,求∠QMC的度数.
(1)、数学思考:请你根据“兴趣小组”的探究思路,直接写出∠EFH,∠BEF,∠DHF之间的数量关系: .(2)、问题解决:“智慧小组”把老师提出的问题作了如下变式:将三角形纸片EFG如图2所示放置,使得点F落在AB,CD区域的外部,FG与AB,CD分别交于点M,H.试探究∠EFH,∠BEF,∠DHF之间的数量关系.请你类比“兴趣小组”的探究思路,解决智慧小组提出的问题.(3)、结论运用:如图3,直线ABCD,∠PND=75°,∠EPF=35°,∠PQM=95°.请你运用问题(1),(2)得到的结论,求∠QMC的度数.