北京市西城区2022-2023学年高一上学期数学期末试卷

试卷更新日期：2023-01-13 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | - 5 \leq x < 1} ， B = {x | x^{2} \leq 9}$ ，则 $A \cup B =$ （）

A、 $[- 5 ， 3]$ B、 $(- 3 ， 1]$ C、 $[- 3 ， 1)$ D、 $[- 3 ， 3]$

查看试题解析
2. 已知命题p： $\exists$ x <1， $x^{2} \leq 1$ ，则 $\neg p$ 为（）

A、 $\forall$ x ≥1， $x^{2}$ ＞ $1$ B、 $\exists$ x <1， $x^{2} > 1$ C、 $\forall$ x <1， $x^{2} > 1$ D、 $\exists$ x ≥1， $x^{2} > 1$

查看试题解析
3. 如图，在平行四边形 $A B C D$ 中， $\vec{A C} - \vec{A B} =$ （）

A、 $\vec{C B}$ B、 $\vec{A D}$ C、 $\vec{B D}$ D、 $\vec{C D}$

查看试题解析
4. 若 $a > b$ ，则下列不等式一定成立的是（）

A、 $\frac{1}{a} < \frac{1}{b}$ B、 $a^{2} > b^{2}$ C、 $e^{- a} < e^{- b}$ D、 $l n a > l n b$

查看试题解析
5. 不等式 $\frac{2 x + 1}{x - 2} \leq 1$ 的解集为（）

A、 $[- 3 ， 2]$ B、 $(- \infty ， - 3]$ C、 $[- 3 ， 2)$ D、 $(- \infty ， - 3] ∪ (2 ， + \infty)$

查看试题解析
6. 正方形 $A B C D$ 的边长为1，则 $| \vec{A B} + 2 \vec{A D} | =$ （）

A、1 B、3 C、 $\sqrt{3}$ D、 $\sqrt{5}$

查看试题解析
7. 某物流公司为了提高运输效率，计划在机场附近建造新的仓储中心．已知仓储中心建造费用C（单位：万元）与仓储中心到机场的距离s（单位： $k m$ ）之间满足的关系为 $C = \frac{800}{s} + 2 s + 2000$ ，则当C最小时，s的值为（）

A、20 B、 $20 \sqrt{2}$ C、40 D、400

查看试题解析
8. 设 $l o g_{2} 3 = a$ ，则 $2^{1 + 2 a} =$ （）

A、8 B、11 C、12 D、18

查看试题解析
9. 已知 $\vec{a}$ 为单位向量，则“ $| \vec{a} + \vec{b} | - | \vec{b} | = 1$ ”是“存在 $λ > 0$ ，使得 $\vec{b} = λ \vec{a}$ ”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
10. 近年来，踩踏事件时有发生，给人们的生命财产安全造成了巨大损失．在人员密集区域，人员疏散是控制事故的关键，而能见度x（单位：米）是影响疏散的重要因素．在特定条件下，疏散的影响程度k与能见度x满足函数关系： $k = {\begin{array}{l} 0.2 ， & x < 0.1 \\ a x^{b} + 1.4 ， & 0.1 \leq x \leq 10 \\ 1 ， & x > 10 \end{array}$ （ $a ， b$ 是常数）．如图记录了两次实验的数据，根据上述函数模型和实验数据，b的值是（参考数据： $l g 3 \approx 0.48$ ）（）

A、 $- 0.24$ B、 $- 0.48$ C、0.24 D、0.48

查看试题解析

二、填空题

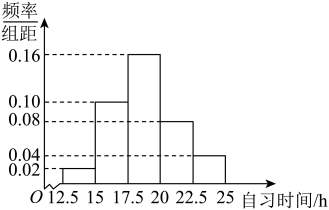
11. 函数 $f (x) = l o g_{2} (1 - x) + \sqrt{x}$ 的定义域是．

查看试题解析
12. 某高校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是 $[12.5 ， 25]$ ，样本数据分组为 $[12.5 ， 15)$ ， $[15 ， 17.5)$ ， $[17.5 ， 20)$ ， $[20 ， 22.5)$ ， $[22.5 ， 25]$ ．根据频率分布直方图，这200名学生中每周的自习时间不少于20小时的人数是．

查看试题解析
13. 写出一个同时满足下列两个条件的函数 $f (x) =$ ．
①对 $\forall x_{1} ， x_{2} \in (0 ， + \infty)$ ，有 $f (x_{1} x_{2}) = f (x_{1}) + f (x_{2})$ ；
②当 $x \in (4 ， + \infty)$ 时， $f (x) > 1$ 恒成立．

查看试题解析
14. 函数 $f (x)$ 的定义域为 $R$ ，且 $\forall x \in R$ ，都有 $f (- x) = \frac{1}{f (x)}$ ，给出给出下列四个结论：
① $f (0) = 1$ 或 $- 1$ ；
② $f (x)$ 一定不是偶函数；
③若 $f (x) > 0$ ，且 $f (x)$ 在 $(- \infty ， 0)$ 上单调递增，则 $f (x)$ 在 $(0 ， + \infty)$ 上单调递增；
④若 $f (x)$ 有最大值，则 $f (x)$ 一定有最小值．
其中，所有正确结论的序号是．

查看试题解析
15. 已知函数 $f (x) = {\begin{array}{l} 2^{x} + a ， x \geq 0 \\ a x ， x < 0 \end{array}$ ，若 $a = - 4$ ，则 $f (x) > 0$ 的解集为；若 $\forall x \in R$ ， $f (x) > 0$ ，则a的取值范围为．

查看试题解析

三、解答题

16. 某射手打靶命中9环、10环的概率分别为0.25，0.2．如果他连续打靶两次，且每次打靶的命中结果互不影响．

(1)、求该射手两次共命中20环的概率；

(2)、求该射手两次共命中不少于19环的概率．

查看试题解析
17. 已知函数 $f (x) = \frac{x}{x^{2} + 1}$ ．

(1)、判断函数 $f (x)$ 的奇偶性，并证明你的结论；

(2)、证明函数 $f (x)$ 在 $[1 ， + \infty)$ 上是减函数；

(3)、写出函数 $f (x)$ 在 $(- \infty ， - 1]$ 上的单调性（结论不要求证明）．

查看试题解析
18. 甲和乙分别记录了从初中一年级（2017年）到高中三年级（2022年）每年的视力值，如下表所示

2017年
2018年
2019年
2020年
2021年
2022年
甲
4.94
4.90
4.95
4.82
4.80
4.79
乙
4.86
4.90
4.86
4.84
4.74
4.72

(1)、计算乙从2017年到2022年这6年的视力平均值；

(2)、从2017年到2022年这6年中随机选取2年，求这两年甲的视力值都比乙高0.05以上的概率；

(3)、甲和乙的视力平均值从哪年开始连续三年的方差最小？（结论不要求证明）

查看试题解析
19. 函数 $f (x) = | 1 - l g x | - c$ ，其中 $c \in R$ ．

(1)、若 $c = 0$ ，求 $f (x)$ 的零点；

(2)、若函数 $f (x)$ 有两个零点 $x_{1} ， x_{2} (x_{1} < x_{2})$ ，求 $4 x_{1} + x_{2}$ 的取值范围．

查看试题解析
20. 某商贸公司售卖某种水果．经市场调研可知：在未来20天内，这种水果每箱的销售利润r（单位：元）与时间t（ $1 \leq t \leq 20 ， t \in N$ ，单位：天）之间的函数关系式为 $r = \frac{1}{4} t + 10$ ，且日销售量p（单位：箱）与时间t之间的函数关系式为 $p = 120 - 2 t$ ．

(1)、求第几天的日销售利润最大？最大值是多少？

(2)、在未来的这20天中，在保证每天不赔本的情况下，公司决定每销售1箱该水果就捐赠 $m (m \in N^{*})$ 元给“精准扶贫”对象，为保证销售积极性，要求捐赠之后每天的利润随时间t的增大而增大，求m的取值范围．

查看试题解析
21. 设函数 $f (x)$ 的定义域为D，对于区间 $I = [a ， b] (a < b ， I \subseteq D)$ ，若满足以下两条性质之一，则称I为 $f (x)$ 的一个“ $Ω$ 区间”．
性质1：对任意 $x \in I$ ，有 $f (x) \in I$ ；
性质2：对任意 $x \in I$ ，有 $f (x) \notin I$ ．

(1)、分别判断区间 $[1 ， 2]$ 是否为下列两函数的“ $Ω$ 区间”（直接写出结论）；
① $y = 3 - x$ ； ② $y = \frac{3}{x}$ ；

(2)、若 $[0 ， m] (m > 0)$ 是函数 $f (x) = - x^{2} + 2 x$ 的“ $Ω$ 区间”，求m的取值范围；

(3)、已知定义在 $R$ 上，且图象连续不断的函数 $f (x)$ 满足：对任意 $x_{1} ， x_{2} \in R$ ，且 $x_{1} \neq x_{2}$ ，有 $\frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}} < - 1$ ．求证： $f (x)$ 存在“ $Ω$ 区间”，且存在 $x_{0} \in R$ ，使得 $x_{0}$ 不属于 $f (x)$ 的所有“ $Ω$ 区间”．

查看试题解析

	2017年	2018年	2019年	2020年	2021年	2022年
甲	4.94	4.90	4.95	4.82	4.80	4.79
乙	4.86	4.90	4.86	4.84	4.74	4.72