山东省聊城市东昌府区2021-2022学年七年级下学期第一次月考数学试题
试卷更新日期:2023-01-13 类型:月考试卷
一、单选题
-
1. 如图,直线AB与CD相交于点O,若 , 则等于( )
 A、40° B、60° C、70° D、80°2. 如图,下列说法错误的是( )
A、40° B、60° C、70° D、80°2. 如图,下列说法错误的是( ) A、也可用来表示 B、与是同一个角 C、图中共有三个角: , , D、与是同一个角3. 如图,O为直线AB上的一点,∠AOC=90°,∠DOE=90°,则图中∠BOE的余角共有( )
A、也可用来表示 B、与是同一个角 C、图中共有三个角: , , D、与是同一个角3. 如图,O为直线AB上的一点,∠AOC=90°,∠DOE=90°,则图中∠BOE的余角共有( )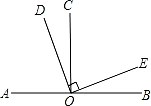 A、1个 B、2个 C、3个 D、4个4. 如图, , , 垂足为点 , 则点到直线的距离是( )
A、1个 B、2个 C、3个 D、4个4. 如图, , , 垂足为点 , 则点到直线的距离是( ) A、线段的长度 B、线段的长度 C、线段的长度 D、线段的长度5. 如图,直线 a、b 被直线 c 所截,下列说法错误的是 ( )
A、线段的长度 B、线段的长度 C、线段的长度 D、线段的长度5. 如图,直线 a、b 被直线 c 所截,下列说法错误的是 ( ) A、∠1 和∠4 是内错角 B、∠2 和∠3 是同旁内角 C、∠1 和∠3 是同位角 D、∠3 和∠4 互为邻补角6. 如图,直线、被直线l所截, , ∠1=α,则∠2的大小为( )
A、∠1 和∠4 是内错角 B、∠2 和∠3 是同旁内角 C、∠1 和∠3 是同位角 D、∠3 和∠4 互为邻补角6. 如图,直线、被直线l所截, , ∠1=α,则∠2的大小为( ) A、α B、2α C、90°+α D、180°-α7. 如图,将三角板的直角顶点放在直尺的一边上.若 , 则的度数为( )
A、α B、2α C、90°+α D、180°-α7. 如图,将三角板的直角顶点放在直尺的一边上.若 , 则的度数为( ) A、45° B、50° C、55° D、65°8. 如图,长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将对折,点B落在直线EF上的点处,得折痕EM;将对折,点A落在直线EF上的点处,得折痕EN,则的度数α.( )
A、45° B、50° C、55° D、65°8. 如图,长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将对折,点B落在直线EF上的点处,得折痕EM;将对折,点A落在直线EF上的点处,得折痕EN,则的度数α.( )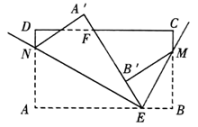 A、 B、 C、 D、α随EF位置的变化而变化9. 如图,∠AOB,以OA为边作∠AOC,使∠BOC= ∠AOB,则下列结论成立的是( )
A、 B、 C、 D、α随EF位置的变化而变化9. 如图,∠AOB,以OA为边作∠AOC,使∠BOC= ∠AOB,则下列结论成立的是( )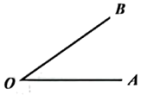 A、 B、 C、 或 D、 或10. 据中国载人航天工程办公室消息,北京时间2021年12月9日15点40分,“天宫课堂”第一课正式开讲.在时刻15:40时,时钟上的时针与分针之间所成的夹角是( )A、150° B、120° C、130° D、140°11. 如图,将一张长方形纸带沿EF折叠,点C、D的对应点分别为、 . 若 , 用含的式子可以将表示为( )
A、 B、 C、 或 D、 或10. 据中国载人航天工程办公室消息,北京时间2021年12月9日15点40分,“天宫课堂”第一课正式开讲.在时刻15:40时,时钟上的时针与分针之间所成的夹角是( )A、150° B、120° C、130° D、140°11. 如图,将一张长方形纸带沿EF折叠,点C、D的对应点分别为、 . 若 , 用含的式子可以将表示为( ) A、 B、 C、 D、12. 下列语句中:①由两条射线组成的图形叫做角;②有公共顶点且相等的角是对项角;③直线外一点到这条直线的垂线段,叫做点到直线的距离;④同位角相等;⑤在平面内,经过一点有且只有一条直线与已知直线垂直;⑥在平面内,经过一点有且只有一条直线与已知直线平行,其中正确的个数有( )A、1个 B、2个 C、3个 D、4个
A、 B、 C、 D、12. 下列语句中:①由两条射线组成的图形叫做角;②有公共顶点且相等的角是对项角;③直线外一点到这条直线的垂线段,叫做点到直线的距离;④同位角相等;⑤在平面内,经过一点有且只有一条直线与已知直线垂直;⑥在平面内,经过一点有且只有一条直线与已知直线平行,其中正确的个数有( )A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 比较大小:(填“>”,“<”或“=”).14. 如图,请添加一个条件,使得 , 添加一个符合要求的条件,可以是.
 15. 生活中常见一种折叠拦道闸,如图1所示.若想求解某些特殊状态下的角度,需将其抽象为几何图形,如图2所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD=°.
15. 生活中常见一种折叠拦道闸,如图1所示.若想求解某些特殊状态下的角度,需将其抽象为几何图形,如图2所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD=°.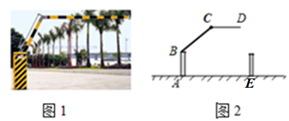 16. 如图,将三角尺与两边平行的直尺(EF∥HG)贴在一起(∠ACB=90°)在直尺的一边上.若∠2=47°,则∠1的大小为 度.
16. 如图,将三角尺与两边平行的直尺(EF∥HG)贴在一起(∠ACB=90°)在直尺的一边上.若∠2=47°,则∠1的大小为 度. 17. 如图,在三角形ABC中,∠ACB=90°,AC=15,BC=20,AB=25,点P为直线AB上的一动点,连接PC,则线段PC的最小值是
17. 如图,在三角形ABC中,∠ACB=90°,AC=15,BC=20,AB=25,点P为直线AB上的一动点,连接PC,则线段PC的最小值是
三、解答题
-
18. 计算:(1)、;(2)、 .19. 如果一个角的补角是这个角的余角的4倍,求这个角.20. 如图,直线AB,CD交于点O,OM⊥AB,ON⊥CD.
 (1)、写出图中所有与∠AOC互余的角.(2)、当∠MON=120°时,求∠BOD的度数.21. 补充下列证明,并在括号内填上推理依据.
(1)、写出图中所有与∠AOC互余的角.(2)、当∠MON=120°时,求∠BOD的度数.21. 补充下列证明,并在括号内填上推理依据.已知:如图,∠AOB+∠BOC=180°,OE平分∠AOB,OF平分∠BOC.求证:OE⊥OF.

证明:∵OE平分∠AOB,OF平分∠BOC,( )
∴∠1=∠AOB,∠2=∠BOC.( )
又∵∠AOB+∠BOC=180°,( )
∴∠1+∠2=(∠AOB+∠BOC)= ▲ °( )
∴OE⊥OF.( )
22. 已知:如图.在△ABC中.点D,E,F分到在边AB,AC,BC上,CD与EF相交于点H,且∠BDC+∠DHF=180°.∠DEF=∠B,求证:DE∥BC. 23. 已知一个角的两边与另一个角的两边分别平行,探索这两个角的关系,并说明理由.
23. 已知一个角的两边与另一个角的两边分别平行,探索这两个角的关系,并说明理由. (1)、如图(一), , , 与的关系是 .(2)、如图(二), , , 与的关系是 .(3)、经过上述证明,我们可以得到一个结论: .(4)、若两个角的两边分别平行,且一个角比另一个角的2倍少30°,则这两个角分别是多少度?
(1)、如图(一), , , 与的关系是 .(2)、如图(二), , , 与的关系是 .(3)、经过上述证明,我们可以得到一个结论: .(4)、若两个角的两边分别平行,且一个角比另一个角的2倍少30°,则这两个角分别是多少度?

