山东省济宁市金乡县2021-2022学年七年级下学期6月月考数学试题
试卷更新日期:2023-01-13 类型:月考试卷
一、单选题
-
1. 在下列实数中,无理数是( )A、 B、 C、0 D、-12. 已知点在第二象限,则点在第( )象限.A、一 B、二 C、三 D、四3. 下列各式是二元一次方程的是( )A、3y+ B、 C、y= D、x2+y=04. 若 ,则下列各式中一定成立的是( )A、 B、 C、 D、5. 下列各组中,互为相反数的一组是( )A、与 B、与 C、3与 D、与36. 如图,天平右盘中的每个砝码的质量都是1g,则物体A的质量m(g)的取值范围在数轴上可表示( )
 A、
A、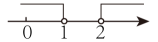 B、
B、 C、
C、 D、
D、 7. 如图,直线 , 一直角三角板ABC(∠ACB=90°)放在平行线上,两直角边分别与、交于点D、E,现测得∠1=75° , 则∠2的度数为( )
7. 如图,直线 , 一直角三角板ABC(∠ACB=90°)放在平行线上,两直角边分别与、交于点D、E,现测得∠1=75° , 则∠2的度数为( ) A、15° B、25° C、30° D、35°8. 《孙子算经》是中国古代重要的数学著作,其中有一段文字的大意是:甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文;如果乙得到甲所有钱的 ,那么乙也共有钱48文,甲、乙两人原来各有多少钱?设甲原有 文钱,乙原有 文钱,可列方程组是( )A、 B、 C、 D、9. 如图所示,如果 AB ∥ CD ,则∠α、∠β、∠γ之间的关系为( )
A、15° B、25° C、30° D、35°8. 《孙子算经》是中国古代重要的数学著作,其中有一段文字的大意是:甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文;如果乙得到甲所有钱的 ,那么乙也共有钱48文,甲、乙两人原来各有多少钱?设甲原有 文钱,乙原有 文钱,可列方程组是( )A、 B、 C、 D、9. 如图所示,如果 AB ∥ CD ,则∠α、∠β、∠γ之间的关系为( )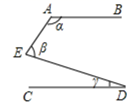 A、∠α+∠β+∠γ=180° B、∠α-∠β+∠γ=180° C、∠α+∠β-∠γ=180° D、∠α-∠β-∠γ=180°[10. 如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆 , , , ……组成一条平滑的曲线.点从原点出发,沿这条曲线向右运动,速度为个单位长度/秒,则第2022秒,点的坐标是( )
A、∠α+∠β+∠γ=180° B、∠α-∠β+∠γ=180° C、∠α+∠β-∠γ=180° D、∠α-∠β-∠γ=180°[10. 如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆 , , , ……组成一条平滑的曲线.点从原点出发,沿这条曲线向右运动,速度为个单位长度/秒,则第2022秒,点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若 , 则x= .12. 如图,在一块长方形草地上原有一条等宽的笔直小路,现在要把这条小路改为同样宽度的等宽弯曲小路,则改造后小路的长度 , 草地部分的面积 . (填“变大”,“不变”或“变小”)
 13. 关于x,y的二元一次方程组的解满足x<y,则a的取值范围是 .14. 已知点A(1,0),B(0,5),C(a,0),如果△ABC的面积为10,则a的值为 .15. 对于实数a,b,定义运算“◆”:a◆b= ,例如4◆3,因为4>3.所以4◆3= =5.若x,y满足方程组 ,则x◆y=.
13. 关于x,y的二元一次方程组的解满足x<y,则a的取值范围是 .14. 已知点A(1,0),B(0,5),C(a,0),如果△ABC的面积为10,则a的值为 .15. 对于实数a,b,定义运算“◆”:a◆b= ,例如4◆3,因为4>3.所以4◆3= =5.若x,y满足方程组 ,则x◆y=.三、解答题
-
16.(1)、;(2)、解方程组: .17. 解不等式组: ,并把它的解集在数轴上表示出来.
 18. 如图:在四边形ABCD中,A、B、C、D四个点的坐标分别是:(-2,0)、(0,6)、(4,4)、(2,0)现将四边形ABCD先向上平移1个单位,再向左平移2个单位,平移后的四边形是A'B'C′D'
18. 如图:在四边形ABCD中,A、B、C、D四个点的坐标分别是:(-2,0)、(0,6)、(4,4)、(2,0)现将四边形ABCD先向上平移1个单位,再向左平移2个单位,平移后的四边形是A'B'C′D' (1)、请画出平移后的四边形A'B'C′D'(不写画法),并写出A'、B'、C′、D'四点的坐标.(2)、若四边形内部有一点P的坐标为(a,b)写点P的对应点P′的坐标.(3)、求四边形ABCD的面积.19. 如图, , 平分 交 于点 ,且 ,求 的度数.
(1)、请画出平移后的四边形A'B'C′D'(不写画法),并写出A'、B'、C′、D'四点的坐标.(2)、若四边形内部有一点P的坐标为(a,b)写点P的对应点P′的坐标.(3)、求四边形ABCD的面积.19. 如图, , 平分 交 于点 ,且 ,求 的度数.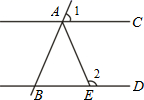 20. 在近几年的两会中,有多位委员不断提出应在中小学开展编程教育,2019年3月教育部公布的《2019年教育信息化和网络安全工作要点》中也提出将推广编程教育.某学校的编程课上,一位同学设计了一个运算程序,如图所示.
20. 在近几年的两会中,有多位委员不断提出应在中小学开展编程教育,2019年3月教育部公布的《2019年教育信息化和网络安全工作要点》中也提出将推广编程教育.某学校的编程课上,一位同学设计了一个运算程序,如图所示.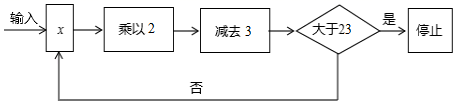
按上述程序进行运算,程序运行到“判断结果是否大于23”为一次运行.
(1)、若x=5,直接写出该程序需要运行多少次才停止;(2)、若该程序只运行了2次就停止了,求x的取值范围.21. 2022年冬奥会吉祥物冰墩墩一夜之间火遍全球,各种冰墩墩的玩偶,挂件,灯饰等应运而生.某学校决定购买A,B两种型号的冰墩墩饰品作为纪念品,已知A种比B种每件多25元,预算资金为1700元:其中800元购买A种商品,其余资金购买B种商品,且购买B种的数量是A种的3倍.(1)、求A,B两种饰品的单价.(2)、购买当日,正逢开学季搞促销,所有商品均按原价八折销售,学校调整了购买方案:不超过预算资金且购买A种饰品的资金不少于720元,A,B两种饰品共100件:问购买A,B两种饰品有哪几种方案?22. 如图,点A在x轴的负半轴上,点D在y轴的正半轴上,将三角形AOD沿x轴向右平移,平移后得到三角形BEC,点A的对应点是点B.已知点A的坐标为(a,0),点C的坐标为(b,c),且a,b,c满足 .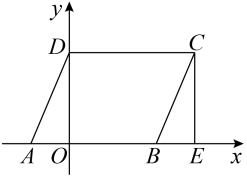 (1)、求点B的坐标;(2)、求证:∠DAE=∠BCD;(3)、点P是线段BC上一动点(不与点B、C重合),连接DP、AP,在点P运动过程中,∠CDP、∠DPA、∠PAE之间是否存在永远不变的数量关系?若存在,写出它们之间的数量关系,并请证明;若不存在,请说明理由.
(1)、求点B的坐标;(2)、求证:∠DAE=∠BCD;(3)、点P是线段BC上一动点(不与点B、C重合),连接DP、AP,在点P运动过程中,∠CDP、∠DPA、∠PAE之间是否存在永远不变的数量关系?若存在,写出它们之间的数量关系,并请证明;若不存在,请说明理由.