内蒙古鄂尔多斯市康巴什区2021-2022学年下学期七年级第二次摸底数学试题
试卷更新日期:2023-01-13 类型:月考试卷
一、单选题
-
1. 下列图形中,可以由其中一个图形通过平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在实数3.1415926, , 0,﹣π,…(相连两个1之间依次多一个0),其中无理数有( )个A、1 B、2 C、3 D、43. 如图,将三角板的直角顶点放在直尺的一边上,若 , 则的度数为( )
2. 在实数3.1415926, , 0,﹣π,…(相连两个1之间依次多一个0),其中无理数有( )个A、1 B、2 C、3 D、43. 如图,将三角板的直角顶点放在直尺的一边上,若 , 则的度数为( ) A、42° B、38° C、52° D、48°4. 、、是直线上的三点,是直线外一点,且 , , . 由此可知,点到直线的距离是( )A、 B、不小于 C、不大于 D、在与之间5. 已知方程组 的解满足x+y=3,则k的值为( ).A、10 B、8 C、2 D、-86. 《九章算术》中的问题:“五只雀,六只燕,共重1斤(古代1斤=16两),雀重燕轻,互换其中一只,恰好一样重,问:每只雀,燕的重量各为多少两?现有列方程求解,设未知数后,小明列出其中一个方程为 , 则另一个方程应为( )A、 B、 C、 D、7. 如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A、42° B、38° C、52° D、48°4. 、、是直线上的三点,是直线外一点,且 , , . 由此可知,点到直线的距离是( )A、 B、不小于 C、不大于 D、在与之间5. 已知方程组 的解满足x+y=3,则k的值为( ).A、10 B、8 C、2 D、-86. 《九章算术》中的问题:“五只雀,六只燕,共重1斤(古代1斤=16两),雀重燕轻,互换其中一只,恰好一样重,问:每只雀,燕的重量各为多少两?现有列方程求解,设未知数后,小明列出其中一个方程为 , 则另一个方程应为( )A、 B、 C、 D、7. 如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )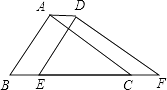 A、6 B、8 C、10 D、128. 估计的值在A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间9. 已知一个正数的两个平方根分别是和 , 求这个数的立方根.( )A、-4 B、10 C、 D、10010. 如图,正方形 , , , …,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为 , , , ; , , , ; , , , ;…)的中心均在坐标原点 , 各边均与轴或轴平行,若它们的边长依次是2,4,6…,则顶点的坐标为( )
A、6 B、8 C、10 D、128. 估计的值在A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间9. 已知一个正数的两个平方根分别是和 , 求这个数的立方根.( )A、-4 B、10 C、 D、10010. 如图,正方形 , , , …,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为 , , , ; , , , ; , , , ;…)的中心均在坐标原点 , 各边均与轴或轴平行,若它们的边长依次是2,4,6…,则顶点的坐标为( )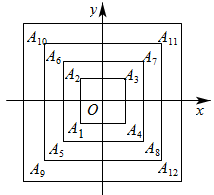 A、(505,505) B、(506,-506) C、(-504,504) D、(-505,-505)
A、(505,505) B、(506,-506) C、(-504,504) D、(-505,-505)二、填空题
-
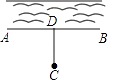
11. 若 是关于x、y的二元一次方程,则a=.12. 已知为的整数部分,是400的算术平方根,则的平方根为 .13. 如图,计划在河边建一水厂,可过C点作CD⊥AB于D点.在D点建水厂,可使水厂到村庄C的路程最短,这样设计的依据是 .
 14. 已知 , , 则 .15. 如图,一张宽度相等的纸条,折叠后,若∠ABC=110°,则∠1的度数为.
14. 已知 , , 则 .15. 如图,一张宽度相等的纸条,折叠后,若∠ABC=110°,则∠1的度数为. 16. 如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①∠BOE=70°;②OF平分∠BOD;③∠1=∠2;④∠POB=2∠3.其中正确的结论有 . (填序号)
16. 如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①∠BOE=70°;②OF平分∠BOD;③∠1=∠2;④∠POB=2∠3.其中正确的结论有 . (填序号)
三、解答题
-
17. 计算:18. 解方程或方程组:(1)、;(2)、 .19. 如图,每个小方格都是边长为1个单位长度的正方形,的顶点都在格点上.
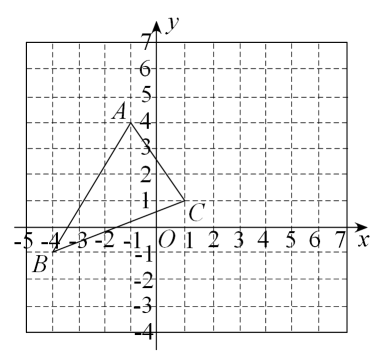 (1)、求三角形的面积;(2)、将平移后得到 , 若此时点的对应点的坐标为 , 请直接写出点的对应点和点的对应点的坐标,并在图中画出;(3)、在轴上是否存在点使得的面积与的面积相等,若存在,求出点坐标,若不存在,请说明理由.20. 如图,在的方格内,填写了一些代数式和数.
(1)、求三角形的面积;(2)、将平移后得到 , 若此时点的对应点的坐标为 , 请直接写出点的对应点和点的对应点的坐标,并在图中画出;(3)、在轴上是否存在点使得的面积与的面积相等,若存在,求出点坐标,若不存在,请说明理由.20. 如图,在的方格内,填写了一些代数式和数. (1)、在图1中各行、各列及对角线上三个数之和都相等,请你求出 , 的值;(2)、把满足(1)的其它6个数填入图2中的方格内.21. 如图, , .
(1)、在图1中各行、各列及对角线上三个数之和都相等,请你求出 , 的值;(2)、把满足(1)的其它6个数填入图2中的方格内.21. 如图, , . (1)、请将下列说明的过程补充完整:
(1)、请将下列说明的过程补充完整:∵(已知)
∴ ▲ ▲ (同位角相等,两直线平行)
∴ ▲ (两直线平行,内错角相等)
又∵(已知)
∴∠ ▲ (等量代换)
∴( )
(2)、如果 , , 求的度数.22. 如图,直线AB、CD相交于点O,OM⊥AB.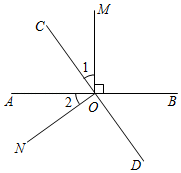 (1)、若∠1=∠2,证明:ON⊥CD;(2)、若∠1∠BOC,求∠BOD的度数.23. 如图1,将两个直角三角板放在同一直线上;其中 , .
(1)、若∠1=∠2,证明:ON⊥CD;(2)、若∠1∠BOC,求∠BOD的度数.23. 如图1,将两个直角三角板放在同一直线上;其中 , .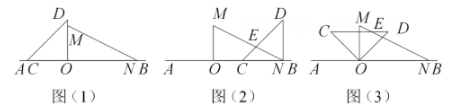 (1)、观察猜想:将图1中的三角板沿直线向右平移至图2的位置,使得点O与点N重合,与相交于点E,则(2)、操作探究:将图1中的三角板绕点O按顺时针方向旋转,使一边在的内部,如图3,且恰好平分 , 与相交于点E,求的度数;(3)、深化拓展:将图1中的三角板绕点O按顺时针方向旋转一周,在旋转的过程中,当边旋转角度为时,边恰好与边平行.(直接写出结果)24. 已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:(1)、1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?(2)、请帮助物流公司设计租车方案(3)、若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.
(1)、观察猜想:将图1中的三角板沿直线向右平移至图2的位置,使得点O与点N重合,与相交于点E,则(2)、操作探究:将图1中的三角板绕点O按顺时针方向旋转,使一边在的内部,如图3,且恰好平分 , 与相交于点E,求的度数;(3)、深化拓展:将图1中的三角板绕点O按顺时针方向旋转一周,在旋转的过程中,当边旋转角度为时,边恰好与边平行.(直接写出结果)24. 已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:(1)、1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?(2)、请帮助物流公司设计租车方案(3)、若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.