北京市丰台区2023届高三上学期数学期末试卷

试卷更新日期：2023-01-13 类型：期末考试

进入出卷网下载

一、单选题

1. 已知全集 $U = R$ ，集合 $A = {x | - 1 < x \leq 0}$ ，则 $∁_{U} A =$ （）

A、 $(- \infty ， - 1) \cup (0 ， + \infty)$ B、 $(- \infty ， - 1] \cup (0 ， + \infty)$ C、 $(- \infty ， - 1) ∪ [0 ， + \infty)$ D、 $(- \infty ， - 1] \cup [0 ， + \infty)$

查看试题解析
2. 已知复数 $z = i (1 + i)$ ，则在复平面内，复数 $\bar{z}$ 对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 在 ${(x - \frac{2}{x})}^{4}$ 的展开式中，常数项为（）

A、 $- 24$ B、24 C、 $- 48$ D、48

查看试题解析
4. 已知向量 $\vec{a} = (2 ， λ) ， \vec{b} = (λ ， 1)$ ，则“ $λ = \sqrt{2}$ ”是“ $\vec{a} / / \vec{b}$ ”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
5. 下列函数是偶函数，且在区间 $(0 ， 1)$ 上单调递增的是（）

A、 $y = 1 - x^{2}$ B、 $y = t a n x$ C、 $y = x c o s x$ D、 $y = e^{x} + e^{- x}$

查看试题解析
6. 已知抛物线 $C ： y^{2} = 2 p x (p > 0)$ 过点 $A (1 ， \sqrt{2})$ ，焦点为F．若点 $B (m ， 0)$ 满足 $| A F | = | B F |$ ，则m的值为（）

A、2 B、 $\sqrt{2} + 1$ C、2或 $- 1$ D、 $\sqrt{2} + 1$ 或 $1 - \sqrt{2}$

查看试题解析
7. 已知函数 $f (x) = 3 l o g_{2} x - 2 (x - 1)$ ，则不等式 $f (x) > 0$ 的解集是（）

A、 $(1 ， 4)$ B、 $(- \infty ， 1) ∪ (4 ， + \infty)$ C、 $(0 ， 1) \cup (4 ， + ∞)$ D、 $(0 ， 4)$

查看试题解析
8. 设双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的右焦点为F，过点F的直线l平行于双曲线C的一条渐近线，与另一条渐近线交于点P，与双曲线C交于点Q，若Q为线段 $F P$ 的中点，则双曲线C的离心率为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2}$ D、 $\frac{4 \sqrt{5}}{5}$

查看试题解析
9. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是边长为3的正方形， $P D ⊥$ 平面 $A B C D$ ，点M为底面上的动点，M到 $P D$ 的距离记为d，若 $| M C | = 2 d$ ，则点M在底面正方形内的轨迹的长度为（）

A、2 B、 $\frac{2 π}{3}$ C、 $\sqrt{5}$ D、 $\frac{3 π}{4}$

查看试题解析
10. 市场占有率指在一定时期内，企业所生产的产品在其市场的销售量（或销售额）占同类产品销售量（或销售额）的比重．一般来说，市场占有率会随着市场的顾客流动而发生变化，如果市场的顾客流动趋向长期稳定，那么经过一段时期以后的市场占有率将会出现稳定的平衡状态（即顾客的流动，不会影响市场占有率），此时的市场占有率称为“稳定市场占有率”．有A，B，C三个企业都生产某产品，2022年第一季度它们的市场占有率分别为：40%，30%，30%．经调查，2022年第二季度A，B，C三个企业之间的市场占有率转移情况如下图所示：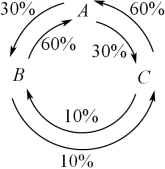
若该产品以后每个季度的市场占有率转移情况均与2022年第二季度相同，则当市场出现稳定的平衡状态，最终达到“稳定市场占有率”时，A企业该产品的“稳定市场占有率”为（）

A、45% B、48% C、50% D、52%

查看试题解析

二、填空题

11. 函数 $f (x) = \frac{1}{2^{x} - 1} + \sqrt{x + 1}$ 的定义域是．

查看试题解析
12. 已知集合 $A = {(x ， y) | x - y - m = 0 ， x ， y \in R}$ ， $B = {(x ， y) | x^{2} + y^{2} - 2 x + 2 y = 0 ， x ， y \in R}$ ，若 $A \cap B$ 为2个元素组成的集合，则实数m的取值范围是．

查看试题解析
13. 已知函数 $f (x) = s i n (ω x + \frac{π}{6}) (ω > 0)$ ，若 $f (\frac{π}{6}) = f (\frac{π}{2})$ ，且 $f (x)$ 在区间 $(\frac{π}{6} ， \frac{π}{2})$ 上有最小值无最大值，则 $ω =$ ．

查看试题解析
14. 已知函数 $f (x) = a l n x - (x - 1)^{2}$ $(a \in R)$ 存在两个极值点 $x_{1} ， x_{2}$ $(x_{1} < x_{2})$ ，给出下列四个结论：
①函数 $f (x)$ 有零点；
②a的取值范围是 $(- \frac{1}{2} ， + \infty)$ ；
③ $x_{2} > 1$ ；
④ $f (x_{2}) > 0$ ．
其中所有正确结论的序号是．

查看试题解析
15. 在等差数列 ${a_{n}}$ 中，公差d不为0， $a_{1} = 9$ ，且 $a_{1} ， a_{4} ， a_{5}$ 成等比数列，则 $d =$ ；当 $n =$ 时，数列 ${a_{n}}$ 的前n项和 $S_{n}$ 有最大值．

查看试题解析

三、解答题

16. 如图，已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点 $E$ 是棱 $B C$ 的中点．

(1)、求证： $B D_{1}$ $∥$ 平面 $D C_{1} E$ ；

(2)、若点F是线段 $B D_{1}$ 的中点，求直线 $D F$ 与平面 $D C_{1} E$ 所成角的正弦值．

查看试题解析
17. 在 $△ A B C$ 中， $2 a s i n B = \sqrt{2} b$ ．

(1)、求A；

(2)、若 $b = 2 \sqrt{2}$ ，从下列三个条件中选出一个条件作为已知，使得 $△ A B C$ 存在且唯一确定，求 $△ A B C$ 的面积．
条件①： $c o s C = - \frac{\sqrt{10}}{10}$ ；
条件②： $a = 2$ ；
条件③： $s i n B = \frac{\sqrt{5}}{5}$ ．
注：如果选择多个条件分别解答，按第一个解答计分．

查看试题解析
18. 非物质文化遗产（简称“非遗”）是优秀传统文化的重要组成部分，是一个国家和民族历史文化成就的重要标志．随着短视频这一新兴媒介形态的兴起，非遗传播获得广阔的平台，非遗文化迎来了发展的春天．为研究非遗短视频受众的年龄结构，现从各短视频平台随机调查了1000名非遗短视频粉丝，记录他们的年龄，将数据分成6组： $[10 ， 20) ， [20 ， 30) ， [30 ， 40) ， [40 ， 50) ， [50 ， 60) ， [60 ， 70]$ ，并整理得到如下频率分布直方图：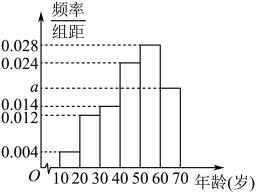

(1)、求a的值；

(2)、从所有非遗短视频粉丝中随机抽取2人，记取出的2人中年龄不超过40岁的人数为X，用频率估计概率，求X的分布列及数学期望 $E (X)$ ；

(3)、在频率分布直方图中，用每一个小矩形底边中点的横坐标作为该组粉丝年龄的平均数，估计非遗短视频粉丝年龄的平均数为m，若中位数的估计值为n，写出m与n的大小关系．（结论不要求证明）

查看试题解析
19. 已知椭圆 $E ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 过点 $A (- 2 ， 0)$ ，离心率为 $\frac{\sqrt{2}}{2}$ ．

(1)、求椭圆E的方程；

(2)、设点 $P (2 ， m) (m > 0)$ ，直线 $P A$ 与椭圆E的另一个交点为C，O为坐标原点，B为椭圆E的右顶点．记直线 $O P$ 的斜率为 $k_{1}$ ，直线 $B C$ 的斜率为 $k_{2}$ ，求证： $k_{1} \cdot k_{2}$ 为定值．

查看试题解析
20. 已知函数 $f (x) = l n x + s i n x$ ．

(1)、求曲线 $y = f (x)$ 在点 $(1 ， f (1))$ 处的切线方程；

(2)、求函数 $f (x)$ 在区间 $[1 ， e]$ 上的最小值；

(3)、证明函数 $f (x)$ 只有一个零点．

查看试题解析
21. 设 $λ$ 为正实数，若各项均为正数的数列 ${a_{n}}$ 满足： $\forall n \in N^{*}$ ，都有 $a_{n + 1} \geq a_{n} + λ$ ．则称数列 ${a_{n}}$ 为 $P (λ)$ 数列．

(1)、判断以下两个数列是否为 $P (2)$ 数列：
数列 $A$ ：3，5，8，13，21；
数列 $B$ ： $l o g_{2} 5$ ， $π$ ， 5，10．

(2)、若数列 ${b_{n}}$ 满足 $b_{1} > 0$ 且 $b_{n + 1} = b_{n} + \sqrt{n + 3} - \sqrt{n + 1}$ ，是否存在正实数 $λ$ ，使得数列 ${b_{n}}$ 是 $P (λ)$ 数列？若存在，求 $λ$ 的取值范围；若不存在，说明理由．

(3)、若各项均为整数的数列 ${a_{n}}$ 是 $P (1)$ 数列，且 ${a_{n}}$ 的前 $m (m \geq 2)$ 项和 $a_{1} + a_{2} + a_{3} + ⋯ + a_{m}$ 为150，求 $a_{m} + m$ 的最小值及取得最小值时 $a_{m}$ 的所有可能取值．

查看试题解析