辽宁省大连市高新园区名校联盟2021-2022学年七年级下学期4月月考数学试题

试卷更新日期：2023-01-13 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列各图中，∠1与∠2是对顶角的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各数是无理数的是（）

A、0 B、-1 C、 $\sqrt{2}$ D、3.14

查看试题解析
3. 如图，直线 $A B$ 和 $C D$ 相交于点 $O$ ， $O E ⊥ A B$ 于点 $O$ ，图中 $∠ 1$ 与 $∠ 2$ 的关系是（）

A、 $∠ 1 + ∠ 2 = 90 °$ B、 $∠ 1 + ∠ 2 = 180 °$ C、 $∠ 1 = ∠ 2$ D、 $∠ 2 = 2 ∠ 1$

查看试题解析
4. 估计 $\sqrt{15}$ 的值在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
5. 下列各式计算正确的是（）

A、 $\sqrt[3]{8} = \pm 2$ B、 $\sqrt[3]{- 1} = - 1$ C、 $\sqrt[3]{9} = 3$ D、 $\sqrt{4} = \pm 2$

查看试题解析
6. 如图，直线 $l_{1}$ 、 $l_{2}$ 被直线l所截， $l_{1} ∥ l_{2}$ ， ∠1=α，则∠2的大小为（）

A、α B、2α C、90°+α D、180°-α

查看试题解析
7. 已知 $\sqrt[3]{1 - a} = - 2$ ，则 $a$ 的平方根为（）

A、2 B、±2 C、±3 D、4

查看试题解析
8. 下列命题中是真命题的是（）

A、相等的角是对顶角 B、无理数就是开方开不尽的数 C、同旁内角互补 D、数轴上的点与实数一一对应

查看试题解析
9. 如图，三角形 $A B C$ 沿 $B C$ 所在直线向右平移得到三角形 $D E F$ ，已知 $E C = 2$ ， $B F = 8$ ，则平移的距离为（）

A、6 B、4 C、3 D、2

查看试题解析
10. 直线 $a$ 、 $b$ 、 $c$ 在同一平面内，下面的四个结论：
$①$ 如果a $∥$ b，a $∥$ c，那么b $∥$ c； $②$ 如果a⊥b， $b ⊥ c$ ，那么a $∥$ c； $③$ 如果a $∥$ b， $b ⊥ c$ ，那么 $a ⊥ c$ ； $④$ 如果 $a$ 与 $b$ 相交， $b$ 与 $c$ 相交，那么 $a$ 与 $c$ 相交．

正确的结论为（）

A、 $① ② ③$ B、 $① ② ④$ C、 $① ③ ④$ D、 $② ③ ④$

查看试题解析

二、填空题

11. 在0，1，-π，-3四个实数中，最小的是．

查看试题解析
12. 若实数x $= - \frac{1}{8}$ ，则x的立方根的值为．

查看试题解析
13. 如图OE⊥AB，O为垂足，∠EOD=25°，则∠AOC=°．

查看试题解析
14. 若 $\sqrt{x - 1} + | y + 2 | = 0$ ，则 ${(x + y)}^{2022} =$ ．

查看试题解析
15. 如图， $A D ∥ B C$ ， BD平分∠ABC，若∠ADB=33°，那么∠A的度数是

查看试题解析
16. 如图，已知AB $∥$ CD， $∠ B A D$ 和 $∠ B C D$ 的平分线交于点 $E$ ， $∠ F B C = n °$ ， $∠ B A D = m °$ ，则 $∠ A E C$ 等于 $° （$ 用含 $m$ 、 $n$ 的式子表示 $）$

查看试题解析

三、解答题

17. 计算： $| \sqrt{5} - 2 | + \sqrt{25} + \sqrt{{(- 2)}^{2}} - \sqrt[3]{- 27}$

查看试题解析
18. 如图，直线AB，CD相交于点O，∠BOE=150°，OA平分∠EOC，求∠BOD的度数.

查看试题解析
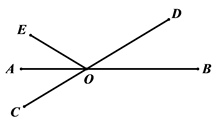19. 已知正数 $m$ 的两个不同的平方根分别是 $a + 3$ 和 $2 a - 15$ ，求 $a$ 和 $m$ 的值．

查看试题解析
20. 如图，在△ABC中，CD平分∠ACB，且∠ECD＝∠EDC．求证：DE $∥$ AC．

查看试题解析
21. 已知 $2 a - 1$ 的算术平方根是3， $3 a + b - 1$ 的立方根是4， $c$ 是 $\sqrt{40}$ 的整数部分，求 $a + b - c$ 的平方根．

查看试题解析
22. 如图， $A B ⊥ B F$ ， $C D ⊥ B F$ ， $∠ 1 = ∠ 2$ ，试说明 $∠ 3 = ∠ E$ ．
证明： $∵ A B ⊥ B F$ ， $C D ⊥ B F （$ 已知 $）$ ，
$∴ ∠ A B D = ∠ C D F = 90 °$ （      ），
$∴ A B$ $∥ C D$ （      ），
$∵ ∠ 1 = ∠ 2$ （已知），
$∴ A B$ $∥ E F$ （已知），
$∴ C D$ $∥ E F$ （      ），
$∴ ∠ 3 = ∠ E$ （      ）

查看试题解析
23. 如图，一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B，点A表示﹣ $\sqrt{2}$ ，设点B所表示的数为m．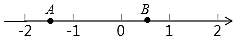

(1)、求实数m的值；

(2)、求|m＋1|＋|m﹣1|的值；

(3)、在数轴上还有C，D两点分别表示实数c和d，且|2c＋d|与 $\sqrt{d^{2} - 16}$ 互为相反数，求2c﹣3d的算术平方根．

查看试题解析
24. 如图，点О在直线AB上， $∠ B O D$ 与 $∠ C O D$ 互补， $∠ B O C = n ∠ E O C$ ．

(1)、若 $∠ A O D = 24 °$ ， $n = 3$ ，求 $∠ D O E$ 的度数；

(2)、若 $D O ⊥ O E$ ，求 $n$ 的值；

(3)、若 $n = 4$ ，设 $∠ A O D = α$ ，求 $∠ D O E$ 的度数（用含 $α$ 的代数式表示 $∠ D O E$ 的度数）．

查看试题解析
25. 如图1，直线MN与直线AB，CD分别交于点E，F， $∠ 1 + ∠ 2 = 180 °$ ．

(1)、求证 $A B ∥ C D$ ；

(2)、如图2， $∠ A E F$ 与 $∠ E F C$ 的角平分线交于点P，延长EP交CD于点G，过G作 $G H ∥ P F$ 交直线MN于点H，求证 $E G ⊥ G H$ ；

(3)、如图3，点P为直线AB，CD之间一点，EQ，FQ分别平分 $∠ P E F$ 和 $∠ C F N$ ，探究 $∠ A E P$ 与 $∠ E Q F$ 之间的数量关系，并证明．

查看试题解析