江西省宜春市袁州区2021-2022学年下学期阶段评估七年级数学试题
试卷更新日期:2023-01-13 类型:月考试卷
一、单选题
-
1. 的相反数是( )A、 B、3.5 C、-7 D、2. 若是关于x,y的二元一次方程,则m-n=( )A、 B、3 C、-1 D、13. 在平面直角坐标系中,若点在第三象限,则m的取值范围为( )A、 B、 C、 D、4. 如图,AB∥CD,BD⊥CF,垂足为B,∠ABF=35°,则∠BDC的度数为( )
 A、25° B、35° C、45° D、55°5. 《九章算术》中有这样一个题:“今有三人共车,二车空;二人共车,九人步.问:人与车各几何?”其大意是:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行,问:人与车各多少?设有 辆车,人数为 ,根据题意,可列二元一次方程组为( )A、 B、 C、 D、6. 在平面直角坐标系中,有三点,其中点A落在y轴上,P为直线AB上的一动点,若PC连线的长度最短,此时点P的坐标为( )A、 B、 C、 D、
A、25° B、35° C、45° D、55°5. 《九章算术》中有这样一个题:“今有三人共车,二车空;二人共车,九人步.问:人与车各几何?”其大意是:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行,问:人与车各多少?设有 辆车,人数为 ,根据题意,可列二元一次方程组为( )A、 B、 C、 D、6. 在平面直角坐标系中,有三点,其中点A落在y轴上,P为直线AB上的一动点,若PC连线的长度最短,此时点P的坐标为( )A、 B、 C、 D、二、填空题
-
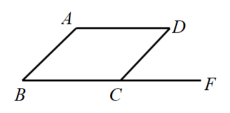
7. 比较大小: . (填“>”、“<”或“=”)8. 对于二元一次方程 , 若 , 则y= .9. 如图, , 要使 , 则的度数为 .
 10. 小贤有一张面值为100元的人民币,需要兑换成面值为5元或10元的零钱,若要求包含两种面值,则共有种兑换方案.11. 若关于x的不等式的解集是 , 则a= .12. 按下面程序计算,若开始输入x的值为大于1的实数,最后得到的结果为290,则符合条件的所有x的值是 .
10. 小贤有一张面值为100元的人民币,需要兑换成面值为5元或10元的零钱,若要求包含两种面值,则共有种兑换方案.11. 若关于x的不等式的解集是 , 则a= .12. 按下面程序计算,若开始输入x的值为大于1的实数,最后得到的结果为290,则符合条件的所有x的值是 .
三、解答题
-
13.(1)、计算:(2)、若正数m的两个平方根分别是和 , 求m的值.14. 解方程组: .15. 解不等式 , 并把解集在数轴上表示出来.16. 如图, , 点E在AC上,连接DE,请仅用无刻度直尺作图.(保留作图痕迹)
 (1)、在图1中作出一个与互补的角.(2)、在图2中,在CD的上方,作出一个与相等的角.17. 利用二元一次方程组解应用题:为有效落实双减工作,切实做到减负提质,很多学校高度重视学生的体育锻炼,并不定期举行体育比赛.已知在一次足球比赛中,胜一场得3分,平一场得1分,负一场得0分,某队在已赛的11场比赛中保持连续不败,共得25分,求该队获胜的场数.18. 下图是某动物园的游览示意图,彤彤同学为了描述该动物园中每个景点的位置,建立了一个平面直角坐标系,每个小方格的边长均为1个单位长度,南门所在的点为坐标原点、飞禽的坐标为 , 请回答下列问题.
(1)、在图1中作出一个与互补的角.(2)、在图2中,在CD的上方,作出一个与相等的角.17. 利用二元一次方程组解应用题:为有效落实双减工作,切实做到减负提质,很多学校高度重视学生的体育锻炼,并不定期举行体育比赛.已知在一次足球比赛中,胜一场得3分,平一场得1分,负一场得0分,某队在已赛的11场比赛中保持连续不败,共得25分,求该队获胜的场数.18. 下图是某动物园的游览示意图,彤彤同学为了描述该动物园中每个景点的位置,建立了一个平面直角坐标系,每个小方格的边长均为1个单位长度,南门所在的点为坐标原点、飞禽的坐标为 , 请回答下列问题. (1)、狮子和马所在的点可用坐标表示为 , .(2)、动物园又来了一位新朋友一大象,若它所在的点的坐标为 .
(1)、狮子和马所在的点可用坐标表示为 , .(2)、动物园又来了一位新朋友一大象,若它所在的点的坐标为 .①请直接在图中标出大象所在的位置.(描出点,并写出“大象”二字)
②丽丽同学建立了一个和彤彤不一样的平面直角坐标系,在丽丽建立的平面直角坐标系中,若飞禽所在的点的坐标是 , 则此时坐标原点是两栖动物所在的点,此时南门所在的点的坐标是 ▲ , 大象所在点的坐标是 ▲ .
19. 解方程组时,两位同学的解法如下.解法一:由①-②,得;
解法二:由②得③,
把①代入③得 .
(1)、反思:上述两种解题过程中你发现解法的解题过程有错误(填“一”或“二”);解二元一次方程组的基本思想是 .(2)、请选择一种你喜欢的方法解此方程组.20. 已知某商场果篮里有水蜜桃、猕猴桃两种水果共85个,设水蜜桃有x个.(1)、小晴说:“猕猴桃是水蜜桃数量的三倍.”小明根据她的说法列出了方程: . 请用小明所列方程分析小晴的说法是否正确.(2)、据商场工作人员透露:猕猴桃比水蜜桃至少多26个,试通过列不等式的方法说明水蜜桃最多有几个.21. 用如图所示的甲、乙、丙木板做一个长、宽、高分别为a厘米,b厘米,h厘米的长方体有盖木箱(),其中甲刚好能做成箱底和一个长侧面,乙刚好能做成一个长侧面和一个短侧面,丙刚好能做成箱盖和一个短侧面.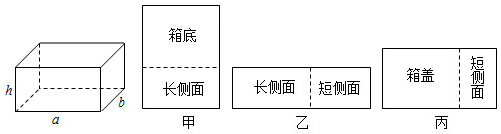 (1)、填空:用含a,b,h的代数式表示以下面积:甲的面积为;乙的面积为;丙的面积为 .(2)、当h=20时,若甲的面积比丙的面积大200cm2 , 乙的面积为1400cm2 , 求a和b的值;22. 如图,MN∥BC,BD⊥DC,∠1=∠2=60°,DC是∠NDE的平分线.
(1)、填空:用含a,b,h的代数式表示以下面积:甲的面积为;乙的面积为;丙的面积为 .(2)、当h=20时,若甲的面积比丙的面积大200cm2 , 乙的面积为1400cm2 , 求a和b的值;22. 如图,MN∥BC,BD⊥DC,∠1=∠2=60°,DC是∠NDE的平分线. (1)、AB与DE平行吗?请说明理由;(2)、试说明:∠ABC=∠C;(3)、求∠ABD的度数.23. 每次重大体育赛事前,电视机的销量都会有一个较大的增长.北京冬奥会前期,某电器商城采购了A,B两种品牌的电视机进行销售,A品牌电视机的进价为2200元/台,B品牌电视机的进价为2000元/台,如图所示的是北京冬奥会前两天两品牌电视机的销售情况:
(1)、AB与DE平行吗?请说明理由;(2)、试说明:∠ABC=∠C;(3)、求∠ABD的度数.23. 每次重大体育赛事前,电视机的销量都会有一个较大的增长.北京冬奥会前期,某电器商城采购了A,B两种品牌的电视机进行销售,A品牌电视机的进价为2200元/台,B品牌电视机的进价为2000元/台,如图所示的是北京冬奥会前两天两品牌电视机的销售情况:销售时段
销售数量(台)
销售收入(元)
A品牌
B品牌
第一天
12
10
63000
第二天
15
12
77400
(1)、求A,B两种品牌的电视机的销售单价.(2)、因为销量比较好,该电器商城打算再次采购这两种品牌的电视机总计30台,若用不多于63700元的金额采购,求A品牌的电视机最多能采购的数量.(3)、在(2)中采购金额下,电器商城销售完这30台电视机能否实现利润超过22650元的目标?若能,请给出相应的采购方案;若不能,请说明理由.