江西省抚州市宜黄县2021-2022学年七年级下学期阶段评估（二）数学试题

试卷更新日期：2023-01-13 类型：月考试卷

进入出卷网下载

一、单选题

1. 2022年是农历壬寅年（虎年），某校师生举办了“迎新春”剪纸活动，下面的剪纸作品是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，由已知条件推出的结论错误的是（）

A、由 $∠ 1 = ∠ 4$ ，可以推出 $A D ∥ B C$ B、由 $∠ B + ∠ B A D = 180 °$ ，可以推出 $A B ∥ D C$ C、由 $A D ∥ B C$ ，可以推出 $∠ B = ∠ 5$ D、由 $A B ∥ D C$ ，可以推出 $∠ 3 = ∠ 2$

查看试题解析
3. 如图，已知△ABC的三条边和三个角，则甲、乙、丙三个三角形中和△ABC全等的是（）

A、甲和乙 B、甲和丙 C、乙和丙 D、只有甲

查看试题解析
4. 如图，将两根钢条 $A A^{'}$ ， $B B^{'}$ 的中点O连在一起，使 $A A^{'}$ ， $B B^{'}$ 可绕点O自由转动，就做成了一个测量工件，则 $A^{'} B^{'}$ 的长等于内槽宽 $A B$ ，那么判定 $△ O A B ≌ △ O A^{'} B^{'}$ 的理由是（）

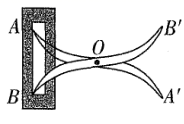A、边角边 B、角边角 C、边边边 D、角角边

查看试题解析
5. 如图，D为 $△ A B C$ 边BC上一动点，将 $△ A B D$ 和 $△ A C D$ 分别以AB，AC为对称轴向外翻折得到 $△ A B E$ 和 $△ A C F$ ，根据图中所标识的角度，则∠EAF的度数为（）

A、104° B、118° C、121° D、138°

查看试题解析
6. 如图，在 $△ A B C$ 中，E是BC上的一点， $E C = 2 B E$ ， D是AC的中点，若四边形EFDC， $△ A D F$ ， $△ A B C$ 的面积分别为 $S_{四边形 E F D C}$ ， $S_{△ A D F}$ ， $S_{△ A B C}$ ，且 $S_{△ A B C} = 18$ ，则 $S_{四边形 E F D C} - S_{△ A B F}$ 等于（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

7. 计算： ${(2 x)}^{3} + {(x - π)}^{0} =$ ．

查看试题解析
8. 如图所示的是一款手机支架，能非常方便地支起手机，由图分析这款手机支架的设计原理是三角形的．

查看试题解析
9. $△ A B C$ 和 $△ A^{'} B^{'} C^{'}$ 关于直线l对称，若 $△ A B C$ 的周长为18cm，则 $△ A^{'} B^{'} C^{'}$ 的周长为．

查看试题解析
10. 将一副三角板按如图所示的位置摆放在直尺上，则∠1的度数为．

查看试题解析
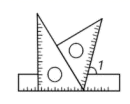11. AD是△ABC的边BC上的中线，AB＝12，AC＝8，则AD的取值范围是．

查看试题解析
12. 如图，直线MN与直线PQ垂直相交于点O，点A在射线OP上运动，点B在射线OM上运动，连接AB，延长BA至点G，已知∠BAO，∠OAG的平分线分别与∠BOQ的平分线及其延长线交于点E，F，在 $△ A E F$ 中，如果有一个角是另一个角的 $\frac{3}{2}$ 倍，则∠ABO的度数为．

查看试题解析

三、解答题

13.

(1)、已知 $a + b + 2 = 0$ ，求 $2^{a} \cdot 2^{b}$ 的值．

(2)、化简： $[{(x + 5 y)}^{2} + (y + x) (y - x)] \div 2 y$ ．

查看试题解析
14. 图1是一款少儿自行车，其U型车架如图2所示，已知 $A B ∥ C D$ ， $∠ A B E = 110 °$ ， $∠ C D E = 120 °$ ，求出∠BED的度数．

查看试题解析
15. 如图，在四边形ABCD中，F是对角线AC的中点， $A D ∥ B C$ ，连接DF并延长交BC边于点E，若 $B E = 6 c m$ ， $A D = 3 c m$ ，试求出BC的长．

查看试题解析
16. 如图， $△ A B C$ 的顶点A，B，C都在方格纸的格点上，试在方格纸上按下列要求作图．

(1)、在图1中作出与 $△ A B C$ 全等的三角形（三角形的顶点在格点上），且有条公共边．

(2)、在图2中作出与 $△ A B C$ 关于直线l对称的三角形 $△ D E F$ ，并用直角三角尺作出 $△ A B C$ 中AB边的高CM．

查看试题解析
17. 某道路安装的护栏平面示意图如图所示，每根立柱宽为0.2米，立柱间距为3米．

(1)、设有x根立柱，护栏总长度为y米，请写出y与x之间的关系式．

(2)、当护栏的总长度为61米时，求出立柱的根数．

查看试题解析
18. 如图，在 $△ A B C$ 中，BD平分∠ABC，E是BC的中点， $E F ⊥ B C$ ，连接CF．若 $∠ A = 70 °$ ，当 $∠ C F D = 52 °$ 时，求∠ACF的度数．

查看试题解析
19. 如图，是一座大楼相邻的两面墙，现需测量外墙根部两点A，B之间的距离(人不能进入墙内测量)．请你按以下要求设计一个方案测量A，B的距离．

(1)、画出测量图案；

(2)、写出简要的方案步骤；

(3)、说明理由．

查看试题解析
20. 如图，把 $△ A B C$ 沿DE折叠，点A落在四边形BCDE外部的点 $A^{'}$ 处．

(1)、由折叠的性质可得≌ ．

(2)、设∠AED的度数为x，∠ADE的度数为y，那么图中∠1，∠2的度数分别是多少？（用含有x或y的式子表示）

(3)、试探究∠A与∠1、∠2之间有何数量关系，并说明理由．

查看试题解析
21. 如图，线段 $A B = 20 m$ ， $M A ⊥ A B$ 于点A， $M A = 6 m$ ，射线 $B D ⊥ A B$ 于点B，点P从点B向点A运动，每秒走1m，点Q从点B向点D运动，每秒走3m．若点P，Q同时从点B出发，当出发t秒后，在线段MA上有一点C，使以点C，A，P为顶点的三角形与 $△ P B Q$ 全等，求t的值．

查看试题解析
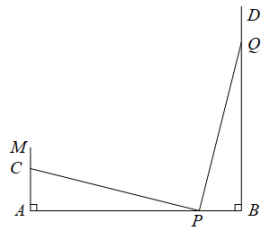22. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ A B C = ∠ A C B = 60 °$ ， D是BC线段上一动点，作 $∠ D A E = 60 °$ ，交BC的延长线于点E，过点B作 $B G ∥ A C$ ，交AD的延长线交于点G．

(1)、BG与CE相等吗？判断并说明理由．

(2)、F为AC上一点， $A F = C E$ ， BF交AD于点H，试猜想AE与AH的数量关系并说明理由．

查看试题解析
23. 综合与探究：
如图1所示的是由两块三角板组成的图形，其中在 $△ A B C$ 中， $∠ C A B = 90 °$ ， $A B = A C (∠ A B C = ∠ A C B = 45 °)$ ，在 $△ A D E$ 中， $∠ D A E = 90 °$ ， $A D = A E (∠ A D E = ∠ A E D = 45 °)$ ，点B，E，D在同一条直线上，AC与BD交于点F，连接CD并延长，交BA的延长线于点G．

(1)、当 $∠ A C D = α$ 时，试用含 $α$ 的代数式表示∠BAE的度数．

(2)、当 $∠ A C D = ∠ C B D$ 时，试探究BC与BG的数量关系，并说明理由．

(3)、过点C作 $C H ∥ B G$ ，交BD的延长线于点H，如图2所示，在满足（2）的情况下，求∠DCH的度数，并直接写出与∠DCH相等的角（除∠G外，写两个即可）．

查看试题解析