北京市朝阳区2022-2023学年高一上学期数学期末试卷
试卷更新日期:2023-01-13 类型:期末考试
一、单选题
-
1. 若 , 则下列各式一定成立的是( )A、 B、 C、 D、2. 若角满足 , 则角是( )A、第一象限角 B、第二象限角 C、第三象限角 D、第四象限角3. 下列函数中,在其定义域上单调递增且值域为的是( )A、 B、 C、 D、4. 设集合 , 集合 , 则A与B的关系为( )A、 B、 C、 D、5. 声强级(单位:)出公式给出,其中I为声强(单位:).若平时常人交谈时的声强约为 , 则声强级为( )A、 B、 C、 D、6. 已知 , ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件7. 已知函数 , 有如下四个结论:
①函数在其定义域内单调递减;
②函数的值域为;
③函数的图象是中心对称图形;
④方程有且只有一个实根.
其中所有正确结论的序号是( )
A、①② B、②③ C、①③ D、③④8. 已知角为第一象限角,且 , 则的取值范围是( )A、 B、 C、 D、9. 某厂以x千克/小时的速度匀速生产某种产品(生产条件要求),每小时可获得利润元,要使生产100千克该产品获得的利润最大,该厂应选取的生产速度是( )A、2千克/小时 B、3千克/小时 C、4千克/小时 D、6千克/小时10. 定义在上的偶函数满足 , 且在上单调递增, , 则a,b,c的大小关系是( )A、 B、 C、 D、二、填空题
-
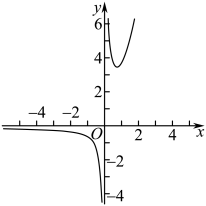
11. 已知集合 , 集合 , 则 .12. 设且 , , 则的最小值为.13. 设函数的定义域为I,如果 , 都有 , 且 , 已知函数的最大值为2,则可以是 .14. 已知下列五个函数: , 从中选出两个函数分别记为和 , 若的图象如图所示,则 .
 15. 已知函数 , 给出以下四个结论:
15. 已知函数 , 给出以下四个结论:①存在实数a,函数无最小值;
②对任意实数a,函数都有零点;
③当时,函数在上单调递增;
④对任意 , 都存在实数m,使方程有3个不同的实根.
其中所有正确结论的序号是 .
16. 已知角 , 若 , 则; .三、解答题
-
17. 已知角的顶点在坐标原点,始边与x轴的非负半轴重合,终边经过点 .(1)、求和的值;(2)、求的值.18. 已知函数 .(1)、当时,解不等式;(2)、若命题“ , 不等式恒成立”是假命题,求实数的取值范围.19. 已知函数 . 从条件①、条件②这两个条件中选择一个作为已知.
条件①:的最大值为6;
条件②:的零点为 .
注:如果选择条件①和条件②分别解答,按第一个解答计分.
(1)、求a的值;(2)、求的最小值,以及取得最小值时x的值.