黑龙江省绥化市绥棱县2021-2022学年七年级下学期第一次月考数学试题

试卷更新日期：2023-01-13 类型：月考试卷

进入出卷网下载

一、填空题

1. 比较大小： $\frac{\sqrt{3}}{2}$ $1$ （填“＞”、“＜”或“＝”）．

查看试题解析
2. －27的立方根与16的算术平方根的和是．

查看试题解析
3. 把命题“两直线平行，同位角相等”改写成“若…，则…” ．

查看试题解析
4. 若AB∥CD，AB∥EF，则CDEF，其理由是.

查看试题解析
5. 如图，直线AB，CD被BC所截，若AB//CD，∠1=45°，∠2=35°，则∠3=度

查看试题解析
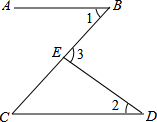6. 如图，AB⊥CD于点B，BE是∠ABD的平分线，则∠CBE的度数为度.

查看试题解析
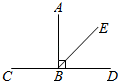7. 如图，数轴上的点A和点B之间的整数点有个．

查看试题解析
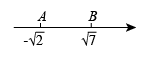8. 对于任意不相等的两个数a，b，定义一种运算※如下：a※b＝ $\frac{\sqrt{a + b}}{a - b}$ ，如3※2＝ $\frac{\sqrt{3 + 2}}{3 - 2}$ ＝ $\sqrt{5}$ .那么12※4＝．

查看试题解析
9. 如果两条平行线被第三条直线所截，一对同旁内角的度数之比是2：7，那么这两个角分别是.

查看试题解析
10. 由下列等式 $\sqrt{2 + \frac{2}{3}}$ =2 $\sqrt{\frac{2}{3}}$ ， $\sqrt{3 + \frac{3}{8}}$ =3 $\sqrt{\frac{3}{8}}$ ， $\sqrt{4 + \frac{4}{15}}$ =4 $\sqrt{\frac{4}{15}}$ …所提示的规律，可得出一般性的结论是(用含n的式子表示)．

查看试题解析

二、单选题

11. 49的平方根是（）

A、7 B、﹣7 C、±7 D、 $\sqrt{49}$

查看试题解析
12. 如图所示的车标，可以看作由平移得到的是（）

A、 B、 C、 D、

查看试题解析
13. 在2， - $\sqrt{2}$ ， 0，1四个实数中，最小的实数是（）

A、2 B、0 C、- $\sqrt{2}$ D、1

查看试题解析
14. 在1， $\frac{22}{7}$ ， $\sqrt{3}$ ， 0.3131131113， $\sqrt[3]{27}$ ， $\frac{π}{2}$ 中，无理数共有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
15. 如图，点 $E$ 在 $C D$ 延长线上，下列条件中不能判定 $A B / / C D$ 的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 3 = ∠ 4$ C、 $∠ 5 = ∠ B$ D、 $∠ B + ∠ B D C = 180 °$

查看试题解析
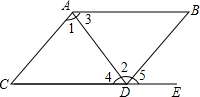16. 如图，△DEF是由△ABC通过平移得到，且点B，E，C，F在同一条直线上．若BF=14，EC=6．则BE的长度是（）

A、1 B、2 C、3 D、4

查看试题解析
17. 下列命题正确的是（）

A、在同一平面内，不重合的两条直线的位置关系有相交、垂直和平行 B、平方根是它本身的数只有0 C、-3²的平方根是±3 D、 $\sqrt{25}$ 的平方根是±5

查看试题解析
18. $\sqrt{61}$ 的整数部分是a，小数部分是b， $a + b$ 等于（）

A、 $\sqrt{61}$ B、 $7 - \sqrt{61}$ C、 $\sqrt{61} - 7$ D、 $\sqrt{61} - 8$

查看试题解析
19.
如图，要把河中的水引到水池A中，应在河岸B处（AB⊥CD）开始挖渠才能使水渠的长度最短，这样做依据的几何学原理是（　　）

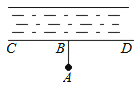A、两点之间线段最短 B、点到直线的距离 C、两点确定一条直线 D、垂线段最短

查看试题解析
20. 如图，将长方形纸片 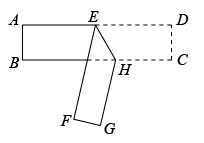$A B C D$ 进行折叠，如果 $∠ B H G = 80 °$ ，那么 $∠ B H E =$ （）度．

A、 $40 °$ B、 $60 °$ C、 $50 °$ D、 $80 °$

查看试题解析

三、解答题

21. 计算．

(1)、 $\sqrt{2} + 3 \sqrt{2} - 5 \sqrt{2}$ ；

(2)、 $\sqrt[3]{8} + \sqrt{(- 2)^{2}} - \sqrt{\frac{1}{4}}$ ．

查看试题解析
22. 解方程：

(1)、 $25 {(x - 1)}^{2} = 49$ ；

(2)、 $64 {(x - 2)}^{3} - 1 = 0$ ．

查看试题解析
23. 如图，直线CD与直线AB相交于C，根据下列语句画图、解答．

⑴过点P作PQ∥CD，交AB于点Q；

⑵过点P作PR⊥CD，垂足为R；

⑶若∠DCB=120°，猜想∠PQC是多少度？并说明理由

查看试题解析
24.
如图，直线AB、CD相交于O，OD平分∠AOF，OE⊥CD于点O，∠1=50°，求∠COB、∠BOF的度数．

查看试题解析
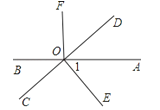25. 如图，E点为DF上的点，B为AC上的点，∠1＝∠2，∠C＝∠D，那么 $D F ∥ A C$ ，请完成它成立的理由．
∵∠1＝∠2
且∠2＝∠3，∠1＝∠4（      ）
∴∠3＝∠4（      ）
∴      ▲ $∥$       ▲ （      ）
∴∠C＝∠ABD（      ）
∵∠C＝∠D（      ）
∴∠D＝∠ABD
∴ $D F ∥ A C$ （      ）．

查看试题解析
26. 已知 $| 2 a + b |$ 与 $\sqrt{3 b + 12}$ 互为相反数．

(1)、求2a－3b的平方根；

(2)、解关于x的方程 $a x^{2} + 4 b - 2 = 0$ ．

查看试题解析
27. 已知图甲是一个长为2m，宽为2n的长方形，沿图甲中虚线用剪刀均匀分成四小块长方形，然后按图乙的形状拼成一个正方形．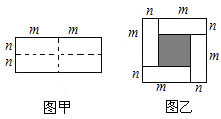

(1)、图乙中阴影部分正方形的边长为（用含字母m，n的整式表示）．

(2)、观察图形，比较图甲、乙中空白部分的面积．直接写出下列三个整式：（m+n）² ，（m-n）² ， mn之间的等量关系．

(3)、解决如下问题：
① $(\sqrt{2} + 1)^{2} - (\sqrt{2} - 1)^{2} =$ ▲
②若a+b=7，ab=5，求a-b的值．

查看试题解析
28. 有一天李小虎同学用“几何画板”画图，他先画了两条平行线AB，CD，然后在平行线间画了一点E，连接BE，DE后（如图①），他用鼠标左键点住点E，拖动后，分别得到如图②，③，④等图形，这时他突然一想，∠B，∠D与∠BED之间的度数有没有某种联系呢？接着小虎同学通过利用“几何画板”的“度量角度”和“计算”功能，找到了这三个角之间的关系．

(1)、你能探究出图①到图④各图中的∠B，∠D与∠BED之间的关系吗？

(2)、请从所得的四个关系中，选一个说明它成立的理由．

查看试题解析