北京市昌平区2022-2023学年高二上学期数学期末质量检测试卷
试卷更新日期:2023-01-13 类型:期末考试
一、单选题
-
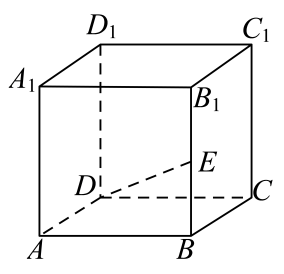
1. 已知直线 , 则直线的倾斜角为( )A、 B、 C、 D、2. 已知 , 且 , 则( )A、 B、2 C、 D、83. 椭圆的右焦点坐标为( )A、 B、 C、 D、4. 已知正方体 , 点是的中点,则( )
 A、 B、 C、 D、5. 在的展开式中,的系数为( )A、 B、 C、90 D、2706. 设是两条不同的直线,是两个不同的平面,下列命题中正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. “”是“双曲线的渐近线方程为”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件8. 已知直线与曲线有公共点,则实数的取值范围是( )A、 B、 C、 D、9. 某社区征集志愿者参加为期5天的“垃圾分类,全民行动”的宣传活动,要求志愿者每人只参加一天且每天至多安排一人.现有甲、乙、丙3人报名,甲要求安排在乙、丙的前面参加活动,那么不同的安排方法共有( )A、18种 B、20种 C、24种 D、30种10. 已知正四棱锥的八条棱长均为是四边形及其内部的点构成的集合.设集合 , 则表示的区域的面积为( )A、 B、 C、 D、
A、 B、 C、 D、5. 在的展开式中,的系数为( )A、 B、 C、90 D、2706. 设是两条不同的直线,是两个不同的平面,下列命题中正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. “”是“双曲线的渐近线方程为”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件8. 已知直线与曲线有公共点,则实数的取值范围是( )A、 B、 C、 D、9. 某社区征集志愿者参加为期5天的“垃圾分类,全民行动”的宣传活动,要求志愿者每人只参加一天且每天至多安排一人.现有甲、乙、丙3人报名,甲要求安排在乙、丙的前面参加活动,那么不同的安排方法共有( )A、18种 B、20种 C、24种 D、30种10. 已知正四棱锥的八条棱长均为是四边形及其内部的点构成的集合.设集合 , 则表示的区域的面积为( )A、 B、 C、 D、二、填空题
-
11. 已知直线.若 , 则实数.12. 从0,2中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,其中偶数共有个.(用数字作答)13. 若 , 则.(用数字作答)14. 数学中有许多形状优美、寓意美好的曲线,曲线就是其中之一(如图).给出下列四个结论:

①曲线有且仅有四条对称轴;
②曲线上任意两点之间的距离的最大值为6;
③曲线恰好经过8个整点(即横坐标、纵坐标均为整数的点);
④曲线所围成的区域的面积大于16.
其中所有正确结论的序号是.
15. 在三棱锥中,底面 , 则异面直线与所成角的大小为;点到平面的距离为.16. 已知双曲线经过点 , 离心率为 , 则双曲线的标准方程为;其焦距为.三、解答题
-
17. 已知圆的圆心坐标为 , 且经过点.(1)、求圆的标准方程;(2)、若过点作圆的切线与轴交于点 , 求直线的方程及的面积.18. 如图,在三棱柱中,平面.
 (1)、求证:平面;(2)、求直线与平面所成角的大小.19. 已知抛物线经过点.(1)、求抛物线的方程及其准线方程;(2)、设 , 直线与抛物线有两个不同的交点.若是以为底边的等腰三角形,求证:直线经过抛物线的焦点.20. 如图,在四棱锥中,底面为平行四边形,平面 , 点在棱上,且平面.
(1)、求证:平面;(2)、求直线与平面所成角的大小.19. 已知抛物线经过点.(1)、求抛物线的方程及其准线方程;(2)、设 , 直线与抛物线有两个不同的交点.若是以为底边的等腰三角形,求证:直线经过抛物线的焦点.20. 如图,在四棱锥中,底面为平行四边形,平面 , 点在棱上,且平面. (1)、求证:是棱的中点;(2)、再从条件①、条件②这两个条件中选择一个作为已知,求:
(1)、求证:是棱的中点;(2)、再从条件①、条件②这两个条件中选择一个作为已知,求:(i)二面角的余弦值;
(ii)在棱上是否存在点 , 使得平面?若存在,求出的值;若不存在,说明理由.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
21. 已知椭圆的离心率为 , 其左、右顶点分别为 , 过点作与轴不重合的直线交椭圆于点(点在轴的上方).(1)、求椭圆的方程;(2)、若线段的长等于 , 求直线的方程;(3)、设直线的斜率分别为 , 试判断是否为定值?若是定值,求出这个定值,并加以证明;若不是定值,说明理由.