河北省定州市2021-2022学年七年级下学期阶段评估(一)数学试题
试卷更新日期:2023-01-13 类型:月考试卷
一、单选题
-
1. 如图,直线a,b相交于点O,∠1=110°,则∠2的度数是( )
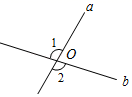 A、70° B、90° C、110° D、130°2. 若 , 则的邻补角的度数为( )A、 B、 C、 D、3. 把如图所示的“调皮”表情进行平移,能得到的图形是( )
A、70° B、90° C、110° D、130°2. 若 , 则的邻补角的度数为( )A、 B、 C、 D、3. 把如图所示的“调皮”表情进行平移,能得到的图形是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,DE∥AB,若∠A = 40°,则∠ACD的度数为( )
4. 如图,DE∥AB,若∠A = 40°,则∠ACD的度数为( ) A、150° B、140° C、50° D、40°5. 如图,将线段向上平移到的位置,若 , 则的度数为( )
A、150° B、140° C、50° D、40°5. 如图,将线段向上平移到的位置,若 , 则的度数为( ) A、 B、 C、 D、6. 如图,与的关系是( )
A、 B、 C、 D、6. 如图,与的关系是( ) A、互为对顶角 B、互为同位角 C、互为内错角 D、互为同旁内角7. 如图,下列条件不能判断的是( )
A、互为对顶角 B、互为同位角 C、互为内错角 D、互为同旁内角7. 如图,下列条件不能判断的是( ) A、 B、 C、 D、8. 判断命题“如果 , 那么”是假命题,只需举一个反例,则a的值可以是( )A、-2 B、0 C、 D、29. 如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )
A、 B、 C、 D、8. 判断命题“如果 , 那么”是假命题,只需举一个反例,则a的值可以是( )A、-2 B、0 C、 D、29. 如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( ) A、如图1,展开后测得∠1=∠2 B、如图2,展开后测得∠1=∠2且∠3=∠4 C、如图3,测得∠1=∠2 D、在图4中,展开后测得∠1+∠2=180°10. 如图,木条a、b、c用螺丝固定在木板上且 , 将木条a、木条b、木条c看作是在同一平面内的三条直线、、 , 若使直线、直线达到平行的位置关系,则下列描述正确的是( )
A、如图1,展开后测得∠1=∠2 B、如图2,展开后测得∠1=∠2且∠3=∠4 C、如图3,测得∠1=∠2 D、在图4中,展开后测得∠1+∠2=180°10. 如图,木条a、b、c用螺丝固定在木板上且 , 将木条a、木条b、木条c看作是在同一平面内的三条直线、、 , 若使直线、直线达到平行的位置关系,则下列描述正确的是( ) A、木条a、c固定不动,木条b绕点E顺时针旋转 B、木条a、c固定不动,木条b绕点E逆时针旋转 C、木条b、c固定不动,木条a绕点B逆时针旋转 D、木条b、c固定不动,木条a绕点B顺时针旋转11. 已知下列命题:
A、木条a、c固定不动,木条b绕点E顺时针旋转 B、木条a、c固定不动,木条b绕点E逆时针旋转 C、木条b、c固定不动,木条a绕点B逆时针旋转 D、木条b、c固定不动,木条a绕点B顺时针旋转11. 已知下列命题:①同一平面内,垂直于同一条直线的两直线平行;②经过直线外一点,有且只有一条直线与这条直线平行;③连接直线外一点与直线上各点的所有线段中,垂线段最短;④同旁内角互补.
其中真命题有( )
A、4个 B、3个 C、2个 D、1个12. 阅读下列材料,其中①~④步数学依据错误的是( )如图:已知直线 , a⊥b,求证: .
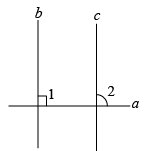
证明:∵(已知),
∴(①垂直的定义).
∵ (已知),
∴(②两直线平行,同位角相等),
∴(③同角的余角相等),
∴(④垂直的定义).
A、① B、② C、③ D、④13. 一副直角三角板如图摆放,其中与交于点M.若 , 则的度数为( ) A、 B、 C、 D、14. 嘉淇在证明“平行于同一条直线的两条直线平行”时,给出了如下推理过程:
A、 B、 C、 D、14. 嘉淇在证明“平行于同一条直线的两条直线平行”时,给出了如下推理过程:已知:如图,b∥a,c∥a,求证:b∥c;
证明:作直线DF交直线a、b、c分
别于点D、E、F,
∵a∥b,∴∠1=∠4,又∵a∥c,
∴∠1=∠5,
∴b∥c.

小明为保证嘉淇的推理更严谨,想在方框中“∴∠1=∠5”和“∴b∥c”之间作补充,下列说法正确的是( )
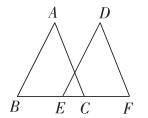
A、嘉淇的推理严谨,不需要补充 B、应补充∠2=∠5 C、应补充∠3+∠5=180° D、应补充∠4=∠515. 如图, , 则、、三者之间的关系是( )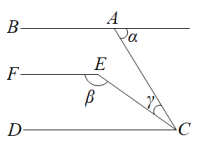 A、 B、 C、 D、16. 如图,在三角形中, , 将三角形以每秒的速度沿线段所在直线向右平移,所得图形对应为三角形 , 设平移时间为t秒 , 若在B,E,C三个点中,其中一个点到另外两个点的距离存在2倍的关系.三人的说法如下:
A、 B、 C、 D、16. 如图,在三角形中, , 将三角形以每秒的速度沿线段所在直线向右平移,所得图形对应为三角形 , 设平移时间为t秒 , 若在B,E,C三个点中,其中一个点到另外两个点的距离存在2倍的关系.三人的说法如下:甲:有两种情况,t的值为2或3.
乙:有三种情况,t的值为2或3或4.
丙:有四种情况,t的值为2或3或4或5.
下列判断正确的是( )
 A、甲对 B、乙对 C、丙对 D、三人都错
A、甲对 B、乙对 C、丙对 D、三人都错二、填空题
-
17. 将命题“等角的补角相等”改写成“如果……那么……”的形式,可写成 , 该命题是(填“真命题”或“假命题”).18. 如图,是的平分线, .
 (1)、的度数为 .(2)、的度数为 .19. 如图,在长方形地块内修筑同样宽的两条“之”字路,余下部分作为耕地.
(1)、的度数为 .(2)、的度数为 .19. 如图,在长方形地块内修筑同样宽的两条“之”字路,余下部分作为耕地.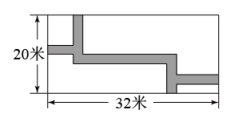 (1)、当修筑的道路宽为2米时,耕地面积为平方米.(2)、当修筑的道路宽为时,道路所占的面积为(用含a的式子表示)平方米.
(1)、当修筑的道路宽为2米时,耕地面积为平方米.(2)、当修筑的道路宽为时,道路所占的面积为(用含a的式子表示)平方米.三、解答题
-
20. 如图, , 求的度数.
 21. 如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
21. 如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
⑴从火车站到码头怎样走最近?画图并说明理由;
⑵从码头到铁路怎样走最近?画图并说明理由;
⑶从火车站到河流怎样走最近?画图并说明理由.
22. 将下面的推理过程及依据补充完整.已知:如图,平分 .

求证:平分 .
证明:∵平分(已知),
∴① ▲ ,
∵(已知),
∴② ▲ (③ ),
∴(等量代换),
∵(已知),
∴④ ▲ (⑤ ),
⑥ ▲ (⑦ ).
∴⑧ ▲ =⑨ ▲ (等量代换),
∴平分 .
23. 如图,在由边长为1的小正方形组成的网格中,平移格点三角形 , 使点A移动到点处. (1)、请画出平移后的三角形并标注字母(点B的对应点为点).(2)、连接 , , 观察发现它们之间具有的关系为(3)、计算三角形的面积.24. 已知如图,直线AB、CD相交于点O,∠COE=90°.
(1)、请画出平移后的三角形并标注字母(点B的对应点为点).(2)、连接 , , 观察发现它们之间具有的关系为(3)、计算三角形的面积.24. 已知如图,直线AB、CD相交于点O,∠COE=90°.
(1)、若∠AOC=36°,求∠BOE的度数;(2)、若∠BOD:∠BOC=1:5,求∠AOE的度数;(3)、在(2)的条件下,过点O作OF⊥AB,请直接写出∠EOF的度数.
25. 如图,直线分别与直线交于点B,F,且 . 的角平分线交直线于点E,的角平分线交直线于点C. (1)、请判断直线与的位置关系,并说明理由.(2)、求证: .(3)、若 , 求的度数.26. 如图,直线AB∥CD,点M,N分别在直线上,H为直线下方一点.
(1)、请判断直线与的位置关系,并说明理由.(2)、求证: .(3)、若 , 求的度数.26. 如图,直线AB∥CD,点M,N分别在直线上,H为直线下方一点.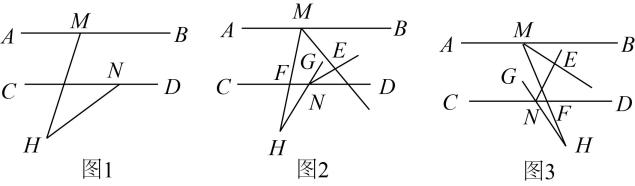 (1)、如图1,和相交于点H,求证: . (温馨提示:可过点H作的平行线)(2)、延长至点G,的平分线和的平分线相交于点E,与相交于点F.
(1)、如图1,和相交于点H,求证: . (温馨提示:可过点H作的平行线)(2)、延长至点G,的平分线和的平分线相交于点E,与相交于点F.①如图2,若 , 求的度数;
②如图2,当点F在点N左侧时,若的度数为 , 的度数为 , 且的值是一个定值,请问的度数是否会随x的变化而发生改变?若不变,求出的度数;若变化,请说明理由.
③如图3,当点N在点F左侧时,②中其他条件不变,请问的度数是否会随x的变化而发生改变?若不变,直接写出的度数;若变化,请说明理由.