广东省揭阳市揭西县2021-2022学年下学期七年级数学第二次质量监测试题
试卷更新日期:2023-01-13 类型:月考试卷
一、单选题
-
1. 以下是清华大学、北京大学、上海交通大学、浙江大学的校徽,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列每组数表示3根小木棒的长度(单位:cm),其中能用3根小木棒搭成一个三角形的是( )A、3,4,7 B、3,4,6 C、5,7,12 D、2,3,63. 小李骑车沿直线旅行,先前进了1000米,休息了一段时间,又原路返回800米,再前进1200米,则他离起点的距离s与时间t的关系示意图是( )A、
2. 下列每组数表示3根小木棒的长度(单位:cm),其中能用3根小木棒搭成一个三角形的是( )A、3,4,7 B、3,4,6 C、5,7,12 D、2,3,63. 小李骑车沿直线旅行,先前进了1000米,休息了一段时间,又原路返回800米,再前进1200米,则他离起点的距离s与时间t的关系示意图是( )A、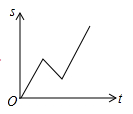 B、
B、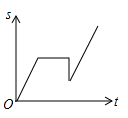 C、
C、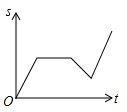 D、
D、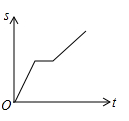 4. 如图,直线 , 直角的直角顶点在直线上,若 , 则的度数为( )
4. 如图,直线 , 直角的直角顶点在直线上,若 , 则的度数为( )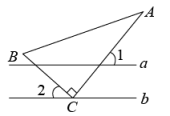 A、 B、 C、 D、5. 下列计算中,正确的是( )A、(a+b)2=a2+b2 B、(a2b)3=a5b3 C、a2+a3=a5 D、(a+2b)(a﹣2b)=a2﹣4b26. 如图,已知AB=AD,AC=AE,若要判定△ABC≌△ADE,则下列添加的条件中正确的是( )
A、 B、 C、 D、5. 下列计算中,正确的是( )A、(a+b)2=a2+b2 B、(a2b)3=a5b3 C、a2+a3=a5 D、(a+2b)(a﹣2b)=a2﹣4b26. 如图,已知AB=AD,AC=AE,若要判定△ABC≌△ADE,则下列添加的条件中正确的是( ) A、∠1=∠DAC B、∠B=∠D C、∠1=∠2 D、∠C=∠E7. 下列说法中,错误的是( )A、平行于同一条直线的两条直线平行 B、在同一平面内,过一点有且只有一条直线与已知直线垂直 C、三角形的高都在三角形内 D、连接直线外一点与直线上各点的所有线段中,垂线段最短8. 如图,下列能判定ABCD的条件有( )个.
A、∠1=∠DAC B、∠B=∠D C、∠1=∠2 D、∠C=∠E7. 下列说法中,错误的是( )A、平行于同一条直线的两条直线平行 B、在同一平面内,过一点有且只有一条直线与已知直线垂直 C、三角形的高都在三角形内 D、连接直线外一点与直线上各点的所有线段中,垂线段最短8. 如图,下列能判定ABCD的条件有( )个.⑴;⑵;⑶;⑷ .
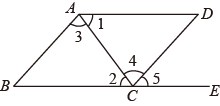 A、1 B、2 C、3 D、49. 如图,在中,分别以点A和点B为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若的周长为17, , 则的周长为( )
A、1 B、2 C、3 D、49. 如图,在中,分别以点A和点B为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若的周长为17, , 则的周长为( ) A、8 B、9 C、10 D、1110. 由图你能根据面积关系得到的数学公式是( )
A、8 B、9 C、10 D、1110. 由图你能根据面积关系得到的数学公式是( )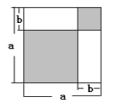 A、a2-b2=(a+b)(a-b) B、(a+b)2=a2+2ab+b2 C、(a-b)2=a2-2ab+b2 D、a(a+b)=a2+ab11. 王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚可以放进一个等腰直角三角板(AC=BC , ∠ACB=90°)点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为( )
A、a2-b2=(a+b)(a-b) B、(a+b)2=a2+2ab+b2 C、(a-b)2=a2-2ab+b2 D、a(a+b)=a2+ab11. 王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚可以放进一个等腰直角三角板(AC=BC , ∠ACB=90°)点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为( ) A、10cm B、14cm C、20cm D、6cm12. 把△ABC和△ADE如图放置,B,D,E正好在一条直线上,AB=AC,AD=AE,∠BAC=∠DAE.则下列结论:①△BAD≌△CAE;②BE=CE+DE;③∠BEC=∠BAC;④若∠ACE+∠CAE+∠ADE=90°,则∠AEC=135°.其中正确的是( )
A、10cm B、14cm C、20cm D、6cm12. 把△ABC和△ADE如图放置,B,D,E正好在一条直线上,AB=AC,AD=AE,∠BAC=∠DAE.则下列结论:①△BAD≌△CAE;②BE=CE+DE;③∠BEC=∠BAC;④若∠ACE+∠CAE+∠ADE=90°,则∠AEC=135°.其中正确的是( ) A、①②③ B、①②④ C、①③④ D、①②③④
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题
-
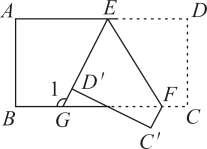
13. 计算 .14. 用科学记数法表示为.15. 若多项式是一个完全平方式,则m的值为 .16. 一个边长为2厘米的正方形,如果它的边长增加 厘米,则面积随之增加y平方厘米,那么y关于x的函数解析式为.17. 如图,将一张长方形纸片沿EF折叠后,点D、C分别落在点、位置,的延长线与BC相交于点G,若 , 则 .
 18. 观察下列图形:已知 , 在第一个图中,可得,则按照以上规律,度.
18. 观察下列图形:已知 , 在第一个图中,可得,则按照以上规律,度.
三、解答题
-
19. 计算:(1)、(2)、 . (用乘法公式简算)20. 先化简,再求值:(x+2)2+(2x+1)(2x﹣1)﹣4x(x+1),其中x=﹣121. 如图,在△ABC中,点D在BC的延长线上, , 且 , . 求证: .
 22. 汽车在山区行驶过程中,要经过上坡、下坡、平路等路段,在自身动力不变的情况下,上坡时速度越来越慢,下坡时速度越来越快,平路上保持匀速行驶,如图表示了一辆汽车在山区行驶过程中,速度随时间变化的情况.
22. 汽车在山区行驶过程中,要经过上坡、下坡、平路等路段,在自身动力不变的情况下,上坡时速度越来越慢,下坡时速度越来越快,平路上保持匀速行驶,如图表示了一辆汽车在山区行驶过程中,速度随时间变化的情况.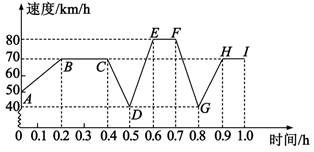 (1)、图中反映哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、汽车在哪些时间段保持匀速行驶?时速分别是多少?(3)、汽车遇到了几个上坡路段?几个下坡路段?在哪个下坡路段上所花时间最长?23. 在△ABC中,BD是边BC上的高.
(1)、图中反映哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、汽车在哪些时间段保持匀速行驶?时速分别是多少?(3)、汽车遇到了几个上坡路段?几个下坡路段?在哪个下坡路段上所花时间最长?23. 在△ABC中,BD是边BC上的高. (1)、尺规作图:作∠C的角平分线,交BD于E.(保留作图痕迹,不写作法,不写结论);(2)、若 , , 求△BCE的面积24. 若x满足 , 求的值.
(1)、尺规作图:作∠C的角平分线,交BD于E.(保留作图痕迹,不写作法,不写结论);(2)、若 , , 求△BCE的面积24. 若x满足 , 求的值.解:设 , , 则 , ,
∴
请仿照上面的方法求解下面问题:
 (1)、若x满足 , 求的值;(2)、已知正方形ABCD的边长为x,E,F分别是AD,DC上的点,且 , , 长方形EMFD的面积是48,分别以MF,DF作正方形MFRN和正方形GFDH,求阴影部分的面积.25. 如图
(1)、若x满足 , 求的值;(2)、已知正方形ABCD的边长为x,E,F分别是AD,DC上的点,且 , , 长方形EMFD的面积是48,分别以MF,DF作正方形MFRN和正方形GFDH,求阴影部分的面积.25. 如图 (1)、如图1,与均是顶角为的等腰三角形,分别是底边,求证:;(2)、如图2,和均为等边三角形,点在同一直线上,连接 .
(1)、如图1,与均是顶角为的等腰三角形,分别是底边,求证:;(2)、如图2,和均为等边三角形,点在同一直线上,连接 .填空:的度数为;线段与之间的数量关系是 .
(3)、拓展探究如图3,和均为等腰直角三角形, , 点在同一直线上,为中边上的高,连接 . 请判断的度数及线段、、之间的数量关系,并说明理由.