安徽省滁州市定远县永康片2021-2022学年七年级下学期第三次教学质量监测数学试题

试卷更新日期：2023-01-13 类型：月考试卷

进入出卷网下载

一、单选题

1. “ $K N 95$ ”表示此类型的口罩能过滤空气中 $95 %$ 的粒径约为 $0.0000003 m$ 的非油性颗粒，其中 $0.0000003$ 用科学记数法表示为（）．

A、 $3 \times 1 0^{- 6}$ B、 $3 \times 1 0^{- 7}$ C、 $0.3 \times 1 0^{- 6}$ D、 $0.3 \times 1 0^{- 7}$

查看试题解析
2. 古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是 $\frac{\sqrt{5} - 1}{2}$ ( $\frac{\sqrt{5} - 1}{2} \approx 0.618$ ，称为黄金比例)，如图，著名的“断臂维纳斯”便是如此，此外，最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是 $\frac{\sqrt{5} - 1}{2}$ ，若某人的身材满足上述两个黄金比例，且头顶至咽喉的长度为 $26 c m$ ，则其升高可能是（）

A、 $165 c m$ B、 $178 c m$ C、 $185 c m$ D、 $190 c m$

查看试题解析
3. 阿慧在店内购买两种蛋糕当伴手礼，如图为蛋糕的价目表．已知阿慧共购买10盒蛋糕，花费的金额不超过500元．若他将蛋糕分给75位同事，每人至少能拿到一个蛋糕，则阿慧花多少元购买蛋糕？（）

A、430 B、450 C、460 D、490

查看试题解析
4. 要使分式 $\frac{x - 2}{(x - 1) (x - 2)}$ 有意义，x的取值应满足（）

A、x≠1 B、x≠2 C、x≠1且x≠2 D、x≠1或x≠2

查看试题解析
5. 下列运算正确的是（）

A、 $(- m)^{3} m^{2} = - m^{6}$ B、 ${(2 a b^{2})}^{3} = 8 a^{3} b^{6}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 ${(\frac{2 a}{b})}^{2} \div \frac{b}{2 a} = \frac{2 a}{b}$

查看试题解析
6. 下列计算正确的是（）

A、 $- 2 x^{2} y^{3} \cdot 2 x^{3} y = - 2 x^{5} y^{4}$ B、 $35 x^{3} y^{2} \div 5 x^{2} y = 7 x y$ C、 $2 m (m n^{2} - 3 m^{2}) = m^{2} n^{2} - 6 m^{3}$ D、 $(- 2 x - y) (2 x + y) = 4 x^{2} - y^{2}$

查看试题解析
7. 若|a|=2， $\sqrt{b}$ =3，ab＜0，则a-b的值为（）

A、-11 B、11 C、1 D、-1

查看试题解析
8. 解不等式组 ${\begin{array}{l} \frac{3 x - 1}{2} > 1 ① \\ 1 - \frac{1}{2} x \leq 0 ② \end{array}$ 时，不等式①②的解集在同一条数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
9. 多项式4x-x³分解因式的结果是（）

A、 $x (4 - x^{2})$ B、 $x (2 - x) (2 + x)$ C、 $x (x - 2) (x + 2)$ D、 $x (2 - x)^{2}$

查看试题解析
10. 在2020年3月底新过肺炎疫情在我国得到快速控制，教育部要求低风险区错时、错峰开学，某校在只有初三年级开学时，一段时间用掉120瓶消毒液，在初二、初一年级也错时、错峰开学后，平均每天比原来多用4瓶消毒液，这样120瓶消毒液比原来少用5天，若设原来平均每天用掉x瓶消毒液，则可列方程是（）

A、 $\frac{120}{x} - 5 = \frac{120}{x + 4}$ B、 $\frac{120}{x - 4} - 5 = \frac{120}{x}$ C、 $\frac{120}{x} + 5 = \frac{120}{x + 4}$ D、 $\frac{120}{x - 4} + 5 = \frac{120}{x}$

查看试题解析

二、填空题

11. 当 $k$ 时， $2 x + k = \frac{1}{3} (x - 4 k) + 6$ 的解是非正数．

查看试题解析
12. 如图，四个完全相同的长方形围一个大正方形，已知每个长方形的周长为60，面积为30，那么图中中间阴影部分的面积为．

查看试题解析
13. 当x的值是时，分式 $\frac{| x | - 3}{2 x - 6}$ 的值为零．

查看试题解析
14. 按照如图所示的流程图，若输出的M＝6，则输入的m是．

查看试题解析

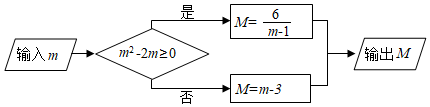
三、解答题

15.

(1)、解方程： $\frac{x + 1}{x - 1} - \frac{4}{x^{2} - 1} = 1$ ．

(2)、先化简，再求值 $(m + 2 - \frac{5}{m - 2}) \cdot \frac{2 m - 4}{3 - m}$ ，其中 $m = - \frac{1}{2}$ ．

查看试题解析
16. 已知不等式组 ${\begin{array}{l} 3 (2 x - 1) < 2 x + 8 ① \\ 2 + \frac{3 (x + 1)}{8} > 3 - \frac{x - 1}{4} ② \end{array}$ ．

(1)、求此不等式组的解集，并写出它的整数解；

(2)、若上述整数解满足不等式 $a x + 6 \leq x - 2 a$ ，化简 $| a + 1 | - | a - 1 |$ ．

查看试题解析
17.

(1)、先完成下列表格：
a
……
0.0001
0.01
1
100
10000
……
$\sqrt{a}$
……
0.01

1

……

(2)、由上表你发现什么规律？

(3)、根据你发现的规律填空：
①已知 $\sqrt{3}$ =1.732则 $\sqrt{300}$ = $\sqrt{0.03}$ =
②已知 $\sqrt{0.003136}$ =0.056，则 $\sqrt{313600}$ =

查看试题解析
18. 截至2022年3月27日，全国累计报告接种新型冠状病毒疫苗超过32亿剂次，为了满足市场需求，某公司计划投入10个大、小两种车间共同生产同一种新型冠状病毒疫苗，已知1个大车间和2个小车间每周能生产疫苗共35万剂，2个大车间和1个小车间每周能生产疫苗共40万剂，每个大车间生产1万剂疫苗的平均成本为90万元，每个小车间生产1万剂疫苗的平均成本为80万元．

(1)、该公司每周每个大车间生产疫苗万剂，每个小车间生产疫苗万剂；

(2)、若所有10个车间全部投入生产，且每周生产的疫苗不少于135 万剂，请问共有几种投入方案，请列出所有正确的方案，并求出每周生产疫苗的总成本最小值．

查看试题解析
19. 规定两数 $a ， b$ 之间的一种运算，记作 $(a ， b)$ ；如果 $a^{c} = b$ ，那么 $(a ， b) = c$ ，例如：因为 $2^{3} = 8$ ，所以 $(2 ， 8) = 3$

(1)、根据上述规定，填空： $(5 ， 125)$ = ； $(5 ， 1)$ = ， $(2 ， \frac{1}{4}) =$ ．

(2)、小明在研究这种运算时发现一个特例：对任意的正整数n， $(3^{n} ， 4^{n}) = (3 ， 4)$ ．小明给了如下的证明：设 $(3^{n} ， 4^{n}) = x ， {(3^{n})}^{x} = 4^{n} ， {(3^{x})}^{n} = 4^{n}$ ，所以 $3^{x} = 4 ， (3 ， 4) = x$ ，所以 $(3^{n} ， 4^{n}) = (3 ， 4)$ ，请根据以上规律：计算： $(16 ， 10000) - (64 ， 1000000)$ ．

(3)、证明下面这个等式： $(3 ， 20) - (3 ， 4) = (3 ， 5)$ ．

查看试题解析
20. 将一张如图①所示的长方形铁皮四个角都剪去边长为30cm的正方形，再四周折起，做成一个有底无盖的铁盒，如图②.铁盒底面长方形的长是4acm，宽是3acm.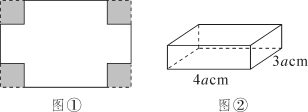

(1)、请用含有a的代数式表示图①中原长方形铁皮的面积；

(2)、若要在铁盒的外表面涂上某种油漆，每1元钱可涂油漆的面积为 $\frac{a}{50}$ cm² ，则在这个铁盒的外表面涂上油漆需要多少钱(用含有a的代数式表示)?

查看试题解析
21. 观察下列一组等式： $(a + 1) (a^{2} - a + 1) = a^{3} + 1$
$(a - 2) (a^{2} + 2 a + 4) = a^{3} - 8$
$(a + 3) (a^{2} - 3 a + 9) = a^{3} + 27$

(1)、以上这些等式中，你有何发现？利用你的发现填空．
① $(x - 3) (x^{2} + 3 x + 9) =$ ；
② $(2 x + 1)$ （） $= 8 x^{3} + 1$ ；
③（） $(x^{2} + x y + y^{2}) = x^{3} - y^{3}$ ．

(2)、利用你发现的规律来计算： $(a + b) (a - b) (a^{2} + a b + b^{2}) (a^{2} - a b + b^{2})$ ．

查看试题解析
22. 观察下列等式：
根据上述规律解决下列问题：
① $1 - 1 - \frac{1}{2} = - \frac{1}{1 \times 2}$ ；
② $\frac{1}{2} - \frac{1}{3} - \frac{1}{4} = - \frac{1}{3 \times 4}$ ；
③ $\frac{1}{3} - \frac{1}{5} - \frac{1}{6} = - \frac{1}{5 \times 6}$ ；
④ $\frac{1}{4} - \frac{1}{7} - \frac{1}{8} = - \frac{1}{7 \times 8}$ ；……

(1)、完成第⑤个等式；

(2)、写出你猜想的第n个等式(用含n的式子表示)并证明其正确性．

查看试题解析
23. 阅读：多项式 $a x + b x + c (a \neq 0) ，$ 当 $a . b . c$ 取某些实数时， $a x^{2} + b x + c$ 是完全平方式．
例如： $a = 1 、 b = - 2 、 c = 1$ 时， $a x^{2} + b x + c = x^{2} - 2 x + 1 = {(x - 1)}^{2}$ ，发现： ${(- 2)}^{2} = 4 \times 1 \times 1$ ；
$a = 1 、 b = 6 、 c = 9$ 时， $a x^{2} + b x + c = x^{2} + 6 x + 9 = {(x + 3)}^{2}$ ，发现： $6^{2} = 4 \times 1 \times 9$ ；
$a = 9 、 b = 12 、 c = 4$ 时， $a x^{2} + b x + c = 9 x^{2} + 12 x + 4 = {(3 x + 2)}^{2}$ ，发现： $1 2^{2} = 4 \times 9 \times 4$ ；
……
根据阅读解答以下问题：

(1)、分解因式： $16 x^{2} - 24 x + 9 =$

(2)、若多项式 $a x^{2} + b x + c (a \neq 0)$ 是完全平方式，则 $a 、 b 、 c$ 之间存在某种关系，用等式表示 $a 、 b 、 c$ 之间的关系：

(3)、在实数范围内，若关于 $x$ 的多项式 $4 x^{2} + m x + 25$ 是完全平方式，求 $m$ 值．

(4)、求多项式： $x^{2} + y^{2} - 4 x + 6 y + 15$ 的最小值．

查看试题解析

a	……	0.0001	0.01	1	100	10000	……
$\sqrt{a}$	……	0.01		1			……