安徽省滁州市定远县吴圩片2021-2022学年七年级下学期5月调研考试数学试题

试卷更新日期：2023-01-13 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列说法中，错误的是（）．

A、4的算术平方根是2 B、8的立方根是 $\pm 2$ C、 $\sqrt{81}$ 的平方根是 $\pm 3$ D、立方根等于－1的实数是－1

查看试题解析
2. 如果 $\sqrt[3]{2.37} = 1.333$ ， $\sqrt[3]{23.7} \approx 2.872$ ，那么 $\sqrt[3]{2370}$ 约等于（）

A、28.72 B、0.2872 C、13.33 D、0.1333

查看试题解析
3. 计算 $(- \frac{1}{2} m n^{3}) \div n^{2}$ 的结果是（）

A、 $- \frac{1}{2} m$ B、 $\frac{1}{2} m$ C、 $- \frac{1}{2} m n$ D、 $\frac{1}{2} m n$

查看试题解析
4. 如图是一个数值转换机，若输入a的值为4，则输出的结果应为（）

A、2 B、-2 C、1 D、-1

查看试题解析
5. 关于x的不等式组 ${\begin{array}{l} 2 x - 3 \geq x - 5 \\ 3 x + a \geq 4 x - 3 \end{array}$ 只有3个整数解，则a的取值范围为（）

A、﹣3≤a＜﹣2 B、﹣3≤a≤﹣2 C、﹣3＜a≤﹣2 D、﹣3＜a＜﹣2

查看试题解析
6. 在边长a为的正方形中挖去一个边长为b的小正方形 $a > b$ （如图1），把余下的部分拼成一个长方形（如图2），根据两个图中阴影部分面积相等，可以验证（）

A、 $(a + 2 b) (a - b) = a^{2} + a b - 2 b^{2}$ B、 $(a - b) (a + b) = a^{2} - b^{2}$ C、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ D、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

查看试题解析
7. 若分式 $\frac{2 x - 2}{x^{2} + 1}$ 的值是负数，则x的取值范围是（）

A、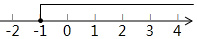 B、 C、 D、

查看试题解析
8. 若 $a = (- \frac{2}{3})^{- 2}$ ， $b = (- 1)^{- 1}$ ， $c = (- \frac{3}{2})^{0}$ ，则 $a$ 、 $b$ 、 $c$ 的大小关系是 $($ $)$

A、 $a > b > c$ B、 $a > c > b$ C、 $c > a > b$ D、 $b > c > a$

查看试题解析
9. 如果一个正整数能表示为两个正整数的平方差，那么这个正整数就称为“智慧数”，例如： $7 = 7 \times 1 = (4 + 3) \times (4 - 3) = 4^{2} - 3^{2}$ ， 7就是一个智慧数， $8 = 4 \times 2 = (3 + 1) \times (3 - 1) = 3^{2} - 1^{1}$ ， 8也是一个智慧数，则下列各数不是智慧数的是（）．

A、2021 B、2022 C、2023 D、2024

查看试题解析
10. 在2020年3月底新过肺炎疫情在我国得到快速控制，教育部要求低风险区错时、错峰开学，某校在只有初三年级开学时，一段时间用掉120瓶消毒液，在初二、初一年级也错时、错峰开学后，平均每天比原来多用4瓶消毒液，这样120瓶消毒液比原来少用5天，若设原来平均每天用掉x瓶消毒液，则可列方程是（）

A、 $\frac{120}{x} - 5 = \frac{120}{x + 4}$ B、 $\frac{120}{x - 4} - 5 = \frac{120}{x}$ C、 $\frac{120}{x} + 5 = \frac{120}{x + 4}$ D、 $\frac{120}{x - 4} + 5 = \frac{120}{x}$

查看试题解析

二、填空题

11. 据悉，世界上最小的开花结果植物是澳大利亚的出水浮萍，这种植物的果实像是一个微小的无花果，质量大约只有 $0.00000000901$ 克，数据 $0.00000000901$ 用科学记数法表示为．

查看试题解析
12. 若 $\sqrt{13}$ 的整数部分为a，小数部分为b，则 $a^{2} + b - \sqrt{13} =$ .

查看试题解析
13. 已知不等式组 ${\begin{array}{l} x + a > 1 \\ 2 x + b < 2 \end{array}$ 的解集为 $- 2 < x < 3$ ，则 $(a + b)^{2021}$ 的值为．

查看试题解析
14. 若 $\frac{1}{x} + \frac{1}{y} = 2$ ，则 $\frac{2 x + x y + 2 y}{3 x + 5 x y + 3 y} =$ ．

查看试题解析

三、解答题

15.

(1)、计算： $| 2 - \sqrt{5} | + {(π - 3)}^{0} - {(\frac{1}{2})}^{- 2} - \sqrt{{(- 3)}^{2}}$ ；

(2)、解不等式： $\frac{y + 1}{3} - \frac{3 y - 5}{2} \geq 4$ ，并将其解集在数轴上表示出来。

查看试题解析
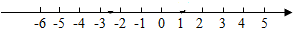16. 先化简，再求值：（ $\frac{a^{2} - 2 a}{a^{2} - 4 a + 4} + \frac{4}{2 - a}$ ）÷ $\frac{a - 4}{a^{2} - 4}$ ，其中a为整数，且a满足2≤a＜5．

查看试题解析
17. 若关于x、y的二元一次方程组 ${\begin{matrix} 2 x + 3 y = 1 \\ 2 x + y = 4 a - 9 \end{matrix}$ 的解满足 $x + y = 1$

(1)、求a的值；

(2)、m为任意实数，当m为何值时， $\sqrt{3 m + a} + 2$ 有最小值？求出这个最小值．

查看试题解析
18. 如图按下列程序进行计算．规定：程序运行到“判断结果是否大于244”为一次运算，结果大于244，则输出此结果；若结果不大于244，则将此结果的值赋给m ，再进行第二次计算．

(1)、当m＝100时，求输出的结果是多少？

(2)、若m＝5，求运算进行多少次才会停止？

(3)、若运算进行了5次才停止．求m的取值范围．

查看试题解析
19. 对于有理数a，b，定义 $m i n {a ， b}$ 的含义为：当 $a \geq b$ 时， $m i n {a ， b} = b$ ；当 $a < b$ 时， $m i n {a ， b} = a$ ．
例如： $m i n {1 ， - 2} = - 2$

(1)、当 $m i n {\frac{2 x - 3}{2} ， \frac{x + 2}{3}} = \frac{x + 2}{3}$ 时，求x的取值范围

(2)、已知 $m i n (\sqrt{31} ， a} = a$ ， $m i n {\sqrt{31} ， b} = \sqrt{31}$ ，且a和b为两个连续正整数，则 $a b - {(\sqrt{31})}^{2}$ 的立方根为多少？

查看试题解析
20. 1261年，我国宋代数学家杨辉写了一本书--《详解九章算法》，书中记载了一个用数字排成的三角形，如图1，这个数字三角形原名“开方作法本源图”，是1050～100年间北宋人贾宪做的．后来，我们就把这种数字三角形叫做贾宪三角或杨辉三角，杨辉三角实际是二项式乘方展开式的系数表，如图2所示．

(1)、写出杨辉三角中的你所发现的规律（1条即可）；

(2)、写出（a+b）⁷展开式中的各项系数；

(3)、已知（x-1）⁶＝ax⁶+bx⁵+cx⁴+dx³+ex²+fx+1，求a+b+c+d+e+f的值．

查看试题解析
21. 【知识回顾】
七年级学习代数式求值时，遇到这样一类题“代数式ax﹣y+6+3x﹣5y﹣1的值与x的取值无关，求a的值”，通常的解题方法是：把x、y看作字母，a看作系数合并同类项，因为代数式的值与x的取值无关，所以含x项的系数为0，即原式＝（a+3）x﹣6y+5，所以a+3＝0，则a＝﹣3．
【理解应用】

(1)、若关于x的多项式（2x﹣3）m+2m²﹣3x的值与x的取值无关，求m值；

(2)、已知A＝（2x+1）（x﹣1）﹣x（1﹣3y），B＝﹣x²+xy﹣1，且3A+6B的值与x无关，求y的值；

(3)、【能力提升】
7张如图1的小长方形，长为a，宽为b，按照图2方式不重叠地放在大长方形ABCD内，大长方形中未被覆盖的两个部分（图中阴影部分），设右上角的面积为S₁ ，左下角的面积为S₂ ，当AB的长变化时，S₁﹣S₂的值始终保持不变，求a与b的等量关系．

查看试题解析
22. 如图是某公司的一份进货单，该公司会计欲查询乙商品的进价，发现进货单已被墨水污染．于是，会计向商品采购员和仓库保管员了解情况．
进货单
进价
数量（元/件）
总金额（件）
商品名称（元）
甲
7200.00
乙
3200.00
商品采购员李阿姨和仓库保管员王师傅对采购情况回忆如下：李阿姨：我记得甲商品进价比乙商品进价每件高50%；王师傅：甲商品比乙商品的数量多40件．请你根据上面的信息，求出乙商品的进价，并帮助他们补全进货单．

查看试题解析
23. 阅读材料：求1+2+2²+2³+2⁴+…+2²⁰¹⁷的值．
解：设S=1+2+2²+2³+2⁴+…+2²⁰¹⁷ ，
将等式两边同时乘以2得：
2S=2+2²+2³+2⁴+…+2²⁰¹⁷+2²⁰¹⁸
将下式减去上式得2S-S=2²⁰¹⁸-1即S=2²⁰¹⁸-1
即1+2+2²+2³+2⁴+…+2²⁰¹⁷=2²⁰¹⁸-1
请你仿照此法计算：

(1)、1+2+2²+2³+…+2⁹=；

(2)、1+5+5²+5³+5⁴+…+5ⁿ(其中n为正整数)；

(3)、1+2×2+3×2²+4×2³+…+9×2⁸+10×2⁹ ．

查看试题解析

进价	数量（元/件）	总金额（件）	商品名称（元）
甲			7200.00
乙			3200.00