初中数学同步训练必刷题（北师大版七年级下册1.7 整式的除法）

试卷更新日期：2023-01-13 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

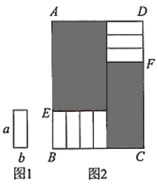
1. 下列计算正确的是（）

A、 $a^{3} \cdot a^{3} = 2 a^{3}$ B、 $x^{2} + x^{2} = x^{4}$ C、 $3 x^{2} \div 2 x = x$ D、 ${(b^{3})}^{2} = b^{6}$

查看试题解析
2. 长方形的面积是3a²－3ab＋6a，一边长为3a，则它的另一条边长为（）

A、2a－b＋2 B、a－b＋2 C、3a－b＋2 D、4a－b＋2

查看试题解析
3. 下列计算不正确的是（）

A、 $m^{2} n^{2} \div m n = m n$ B、 $m^{2} n \cdot m n^{2} = m^{3} n^{3}$ C、 $(m n)^{3} = m^{3} n^{3}$ D、 $(m^{2} n^{3})^{4} = m^{6} n^{7}$

查看试题解析
4. （） $\times a b = 2 a b^{2}$ ，则括号内应填的单项式是（）

A、2 B、2a C、2b D、4b

查看试题解析
5. 计算多项式 $6 x^{2} + 4 x$ 除以 $2 x^{2}$ 后，得到的余式为何？（）

A、2 B、4 C、 $2 x$ D、 $4 x$

查看试题解析
6. 计算（3x²y﹣xy²+ $\frac{1}{2}$ xy）÷（ $\frac{1}{2}$ xy）的结果为（）

A、﹣6x+2y﹣1 B、﹣6x+2y C、6x﹣2y D、6x﹣2y+1

查看试题解析
7. 若 $A$ 与 $- \frac{1}{2} a b$ 的积为 $- 4 a^{3} b^{3} + 3 a^{2} b^{2} - \frac{1}{2} a b$ ，则 $A$ 为（）

A、 $- 8 a^{2} b^{2} + 6 a b - 1$ B、 $- 2 a^{2} b^{2} + \frac{3}{2} a b + \frac{1}{4}$ C、 $8 a^{2} b^{2} - 6 a b + 1$ D、 $2 a^{2} b^{2} - \frac{3}{2} a b + 1$

查看试题解析
8. 计算 ${(- a^{2} b)}^{6} \div (- a)^{3}$ 的结果为（）

A、 $- a^{12} b^{3}$ B、 $- a^{9} b^{6}$ C、 $a^{9} b^{6}$ D、 $- a^{6} b^{6}$

查看试题解析
9. 某天数学课上，老师讲了单项式乘多项式，放学回到家，小明拿出课堂笔记复习，发现一道题：- $3 x y (4 y - 2 x -$ $1) = - 12 x y^{2} + 6 x^{2} y + □ ， □$ 的地方被钢笔水弄污了，你认为 $□$ 内应填写（）

A、3xy B、 $- 3 x y$ C、-1 D、1

查看试题解析
10. 将7张如图1的两边长分别为a和b（ $a \geq b$ ， a与b都为正整数）的矩形纸片按图2的方式不重叠地放在矩形 $A B C D$ 内，矩形中未被覆盖的部分用阴影表示，设左上角与右下角的阴影部分的面积相等.设 $\frac{a}{b} = k$ .若 $A B = 3$ ， k为整数，则a可取的值的个数为（）

A、0个 B、4个 C、5个 D、无数个

查看试题解析

二、填空题（每题3分，共30分）

11. 计算（-2a²）³÷a³的结果是．

查看试题解析
12. $(a b^{2} - 2 a^{2} b + a b) \div a b =$ .

查看试题解析
13. 已知一个长方形的面积是 $4 x^{2} + 2 x$ ，宽为 $2 x$ ，那么它的长为．

查看试题解析
14. 任意给一个非零数m，按下列程序进行计算，则输出结果为；

查看试题解析
15. 利用图1中边长分别为a，b的正方形，以及长为a，宽为b的长方形卡片若干张拼成图2（卡片间不重叠、无缝隙），那么图2这个几何图形表示的可以等式是．

查看试题解析
16. 若n是正整数，且x²ⁿ=6，则（2x³ⁿ）³÷（6x⁵ⁿ）= ．

查看试题解析
17. 如图，一个长、宽、高分别为a，b， $2 r$ 的长方体纸盒装满了一层半径为r的小球，则纸盒的空间利用率（小球总体积与纸箱容积的比）为（结果保留 $π$ ，球体积公式 $V = \frac{4}{3} π r^{3}$ ）．

查看试题解析
18. 若关于x的多项式 $(17 x^{2} - 3 x + 4) - (a x^{2} + b x + c)$ 除以 $5 x$ ，所得商恰好为 $2 x + 1$ ，则 $a + b + c =$ .

查看试题解析
19. 下列运算：① $2 x^{- 5} - 3 x^{- 5} = - \frac{1}{x^{5}}$ ；② ${(x^{- 2})}^{- 3} \cdot {(- 2 x y^{- 2})}^{2} = \frac{4 x^{8}}{y^{4}}$ ；③ ${(- x^{- 4})}^{2} = - \frac{1}{x^{6}}$ ；④ $(- 3 x^{- 2} y) \div x^{- 3} y^{- 2} = - \frac{3 y^{3}}{x}$ ．其中正确的是．

查看试题解析
20. 老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个多项式，形式如下：
$\times (- \frac{1}{2} x y) = 3 x^{2} y - x y^{2} + \frac{1}{2} x y ，$

则当 $x = \frac{2}{3} ， y = \frac{1}{2}$ 时，所捂多项式的值是

查看试题解析

三、解答题（共6题，共60分）

21. 化简：

(1)、（12x²y³﹣8x³y²z）÷4x²y²

(2)、4（x+1）²﹣（2x+5）（2x﹣5）

查看试题解析
22. 化简： $[(2 a + b) (2 a - b) - 4 {(a - b)}^{2} - b^{2}] \div (- 2 b)$ ．

查看试题解析
23. 小明在做一个多项式除以 $\frac{1}{2}$ a的题时，由于粗心误认为乘 $\frac{1}{2}$ a，结果是8a⁴b-4a³+2a² ，那么你能知道正确的结果是多少吗？

查看试题解析
24. 某天数学课上，小明学习了整式的除法运算，放学后，小明回到家拿出课堂笔记，认真地复习课上学习的内容.他突然发现一道三项式除法运算题：（21x⁴y³-+7x²y²）÷（-7x²y）=+5xy-y，被除式的第二项被墨水弄污了，商的第一项也被墨水弄污了，你能算出两处被污染的内容是什么吗?

查看试题解析
25. 发现：一个三位数的百位上数字为a，十位上数字为(a+1)，个位上数字为(a＋2)；把这个三位数的百位上数字与个位上的数字交换得到一个新三位数，新三位数与原三位数的差是9的倍数．
验证：

(1)、①765—567=9× ；

②通过列式计算，说明新三位数与原三位数的差是9的倍数；

(2)、延伸：新三位数与原三位数的和是正整数m的倍数，则m=____________，并说明理由．

查看试题解析
26. 数学是研究现实世界的数量关系与空间形式的科学，同学们，下面我们就用数形结合思想来解决下面问题吧！

(1)、将图①甲中阴影部分的小长方形变换到图乙位置，你根据两个图形的面积关系得到的数学公式是．

(2)、将图②甲中阴影部分的一个小长方形变换到图乙位置，你根据两个图形的面积关系写出一个等式：（a﹣b）（）＝a²+ab﹣ ．

(3)、若把（2）中你写出的等式当做公式用，计算：（x﹣y）[（x+2y）⁴÷（x+2y）³]；

(4)、图③甲是一个长为2a，宽为2b（a＞b）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图③乙那样拼成一个正方形，则图③乙中间空余的部分的面积是．

(5)、观察图③乙，请你写出三个代数式（a+b）²（a﹣b）² ， ab之间的等量关系是．根据（5）中等量关系解决如下问题：若m+n＝﹣7，mn＝3.25，求m﹣n的值．

查看试题解析