山西省大同市杨高县2021-2022学年八年级下学期第二次学情监测(月考)数学试题
试卷更新日期:2023-01-13 类型:月考试卷
一、单选题
-
1. 下图分别给出了变量x与y之间的对应关系,其中y是x的函数是( )A、
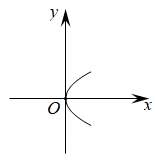 B、
B、 C、
C、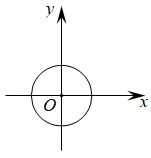 D、
D、 2. 某班同学在“做环保护航者”的主题班会课上制作象征“健康快乐”的绿丝带(丝带的对边平行且宽度相同),如图,丝带重叠的部分一定是( )
2. 某班同学在“做环保护航者”的主题班会课上制作象征“健康快乐”的绿丝带(丝带的对边平行且宽度相同),如图,丝带重叠的部分一定是( ) A、正方形 B、矩形 C、菱形 D、都有可能3. 函数自变量x的取值范围是( )A、 B、 C、 D、4. 已知点和点是一次函数图象上的两点,则与的大小关系是( )A、 B、 C、 D、5. 已知一次函数的图象与直线平行,且过点 , 那么此一次函数的解析式为( ).A、 B、 C、 D、6. 如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )
A、正方形 B、矩形 C、菱形 D、都有可能3. 函数自变量x的取值范围是( )A、 B、 C、 D、4. 已知点和点是一次函数图象上的两点,则与的大小关系是( )A、 B、 C、 D、5. 已知一次函数的图象与直线平行,且过点 , 那么此一次函数的解析式为( ).A、 B、 C、 D、6. 如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( ) A、13 B、14 C、15 D、167. 一次函数y=kx+b(k≠0)的图象如图所示,当y>0时,x的取值范围是( )
A、13 B、14 C、15 D、167. 一次函数y=kx+b(k≠0)的图象如图所示,当y>0时,x的取值范围是( ) A、x>0 B、x<0 C、x>-1 D、x>28. 若实数a、b满足ab<0,则一次函数y=ax+b的图象可能是( )A、
A、x>0 B、x<0 C、x>-1 D、x>28. 若实数a、b满足ab<0,则一次函数y=ax+b的图象可能是( )A、 B、
B、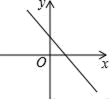 C、
C、 D、
D、 9. 已知一次函数与一次函数的图象的交点在第三象限,则方程组的解可能是( )A、 , B、 , C、 , D、 ,10. 正方形 , 按如图所示的方式放置,点在直线 , 点在x轴上,已知点 , , 则的坐标是( )
9. 已知一次函数与一次函数的图象的交点在第三象限,则方程组的解可能是( )A、 , B、 , C、 , D、 ,10. 正方形 , 按如图所示的方式放置,点在直线 , 点在x轴上,已知点 , , 则的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如果函数y=(m+1)x+m2-1是正比例函数.则m的值是 .12. 已知平行四边形ABCD的两条对角线相交于平面直角坐标系中的原点O,点A(-1,3),则点C的坐标为 .13. 在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图, 是平行四边形 的对角线,点 在 上, , ,则 的大小是.
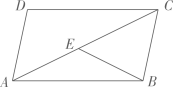 14. 如图,已知正比例函数y1=ax与一次函数y2=-x+b的图象交于点P下面有四个结论:①a>0;②b<0;③当x<0时,y1<0;④当x>2时,y1<y2 . 其中正确的序号是
14. 如图,已知正比例函数y1=ax与一次函数y2=-x+b的图象交于点P下面有四个结论:①a>0;②b<0;③当x<0时,y1<0;④当x>2时,y1<y2 . 其中正确的序号是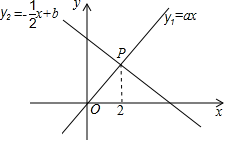 15. 在平面直角坐标系xOy中,直线y=kx+4与x,y轴分别交于点A,B,若将该直线向右平移5单位,线段AB扫过区域的边界恰好为菱形,则k的值为 .
15. 在平面直角坐标系xOy中,直线y=kx+4与x,y轴分别交于点A,B,若将该直线向右平移5单位,线段AB扫过区域的边界恰好为菱形,则k的值为 .三、解答题
-
16. 一次函数(k,b是常数,且)的图象如图所示.
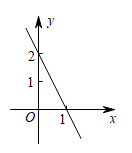 (1)、求k,b的值;(2)、利用图象,直接写出关于x的不等式的解集.17. 为了解某品牌轿车的耗油情况,将油箱加满后进行了耗油试验,得到如表数据:
(1)、求k,b的值;(2)、利用图象,直接写出关于x的不等式的解集.17. 为了解某品牌轿车的耗油情况,将油箱加满后进行了耗油试验,得到如表数据:轿车行驶的路程s(km)
0
100
200
300
400
…
油箱剩余油量Q(L)
50
42
34
26
18
…
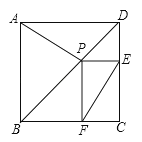
(1)、该轿车油箱的容量为L,行驶200km时,油箱剩余油量为L;(2)、根据上表的数据,写出油箱剩余油量Q(L)与轿车行驶的路程s(km)之间的表达式;(3)、某人将油箱加满后,驾驶该轿车从A地前往B地,到达B地时邮箱剩余油量为24L,求A,B两地之间的距离.18.已知:P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足.
求证:AP=EF.
 19. 如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数图象经过点B(-2,-1)与x轴的交点为C.
19. 如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数图象经过点B(-2,-1)与x轴的交点为C. (1)、求一次函数的解析式;(2)、求△AOC的面积.20. 如图1,矩形的四边上分别有E,F,G,H四点,顺次连接四点得到四边形 . 若 , 则四边形为矩形的“反射四边形”.
(1)、求一次函数的解析式;(2)、求△AOC的面积.20. 如图1,矩形的四边上分别有E,F,G,H四点,顺次连接四点得到四边形 . 若 , 则四边形为矩形的“反射四边形”.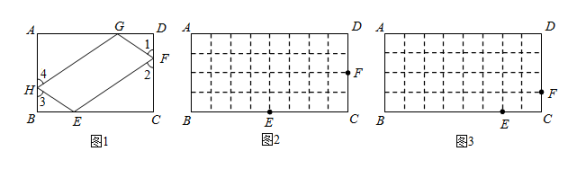 (1)、请分别在图2、图3中画出矩形的“反射四边形”;(2)、若 , , 请计算图3中“反射四边形”的周长.21. 随着“一带一路”的进一步推进,我国瓷器更是“一带一路”沿线人民所推崇的,某商户看准这一商机,准备经销瓷器茶具,计划购进青瓷茶具和白瓷茶具共80套.已知青瓷茶具每套280元,白瓷茶具每套250元,设购进x套青瓷茶具,购进青瓷茶具和白瓷茶具的总费用为y.(1)、求出y与x之间的函数关系式;(2)、该商户想要用不多于20900元的钱购进这两种茶具,且购买白瓷茶具的数量不超过青瓷茶具的两倍,请问有哪几种购进方案.22. 已知,四边形中,点关于的对称点为 , 连接、 , 交于点 .(1)、如图1,当四边形为矩形时,请直接写出与的数量关系;
(1)、请分别在图2、图3中画出矩形的“反射四边形”;(2)、若 , , 请计算图3中“反射四边形”的周长.21. 随着“一带一路”的进一步推进,我国瓷器更是“一带一路”沿线人民所推崇的,某商户看准这一商机,准备经销瓷器茶具,计划购进青瓷茶具和白瓷茶具共80套.已知青瓷茶具每套280元,白瓷茶具每套250元,设购进x套青瓷茶具,购进青瓷茶具和白瓷茶具的总费用为y.(1)、求出y与x之间的函数关系式;(2)、该商户想要用不多于20900元的钱购进这两种茶具,且购买白瓷茶具的数量不超过青瓷茶具的两倍,请问有哪几种购进方案.22. 已知,四边形中,点关于的对称点为 , 连接、 , 交于点 .(1)、如图1,当四边形为矩形时,请直接写出与的数量关系;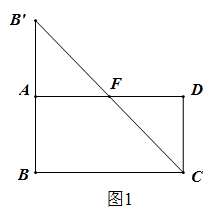 (2)、如图2,当四边形为平行四边形时,①(1)题中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;
(2)、如图2,当四边形为平行四边形时,①(1)题中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;
②如图3,当时,、的延长线相交于点 , 请直接写出的值.
 23. 直线y=﹣x+6与x轴交于A,与y轴交于B,直线CD与y轴交于C(0,2)与直线AB交于D,过D作DE⊥x轴于E(3,0).
23. 直线y=﹣x+6与x轴交于A,与y轴交于B,直线CD与y轴交于C(0,2)与直线AB交于D,过D作DE⊥x轴于E(3,0). (1)、求直线CD的函数解析式;(2)、P是线段OA上一动点,点P从原点O开始,每秒一个单位长度的速度向A运动(P与O,A不重合),过P作x轴的垂线,分别与直线AB,CD交于M,N,设MN的长为S,P点运动的时间为t,求出S与t之间的函数关系式(写出自变量的取值范围)(3)、在(2)的条件下,当t为何值时,以M,N,E,D为顶点的四边形是平行四边形.(直接写出结果)
(1)、求直线CD的函数解析式;(2)、P是线段OA上一动点,点P从原点O开始,每秒一个单位长度的速度向A运动(P与O,A不重合),过P作x轴的垂线,分别与直线AB,CD交于M,N,设MN的长为S,P点运动的时间为t,求出S与t之间的函数关系式(写出自变量的取值范围)(3)、在(2)的条件下,当t为何值时,以M,N,E,D为顶点的四边形是平行四边形.(直接写出结果)