山东省济宁市微山县2021-2022学年八年级下学期数学第一次学情调研试题

试卷更新日期：2023-01-13 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列式子中，一定是二次根式的是（）

A、 $\sqrt{- x - 2}$ B、 $\sqrt{x}$ C、 $\sqrt{x^{2} + 1}$ D、 $\sqrt{x^{2} - 2}$

查看试题解析
2. 下列各组数中，能构成直角三角形的是（）

A、4，5，6 B、1，1， $\sqrt{2}$ C、6，8，11 D、5，12，23

查看试题解析
3. 若 $\sqrt{3}$ 的整数部分为x，小数部分为y，则 $\sqrt{3} x - y$ 的值是（　　）

A、 $3 \sqrt{3} - 3$ B、 $\sqrt{3}$ C、1 D、3

查看试题解析
4. 给出下列命题：①在直角三角形ABC中，已知两边长为3和4，则第三边长为5；②三角形的三边a、b、c满足a²+c²=b² ，则∠C=90°；③△ABC中，若∠A：∠B：∠C=1：5：6，则△ABC是直角三角形；④△ABC中，若 a：b：c=1：2： $\sqrt{3}$ ，则这个三角形是直角三角形.其中，正确命题的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图，在一块平地上，张大爷家屋前9m远处有一棵大树，在一次强风中，这棵大树从离地面6m处折断倒下，量得倒下部分的长是10m，大树倒下时能砸到张大爷的房子吗？（）

A、一定不会 B、可能会 C、一定会 D、以上答案都不对

查看试题解析
6. 如图所示，将矩形ABCD沿AE向上折叠，使点B落在DC边上的F处，AB=10，BC=6，则EF的长为（）

A、 $\frac{10}{3}$ B、3 C、2 D、1

查看试题解析
7. 对于任意的正数m，n定义运算※为：m※n＝ ${\begin{matrix} \sqrt{m} - \sqrt{n} (m \geq n) \\ \sqrt{m} + \sqrt{n} (m < n) \end{matrix}$ 计算(3※2)×(8※12)的结果为（）

A、2－4 $\sqrt{6}$ B、2 C、2 $\sqrt{5}$ D、20

查看试题解析
8. 四边形ABCD中，对角线AC、BD相交于点O，给出下列四个条件：①AD∥BC；②AD=BC；③OA=OC；④OB=OD，从中任选两个条件，能使四边形ABCD为平行四边形的选法有（）．

A、3种 B、4种 C、5种 D、6种

查看试题解析
9. 如图，在平行四边形ABCD中，对角线AC、BD相交于O，过点O作OE⊥AC交AD于E，若AE＝4，DE＝2，AB＝2 $\sqrt{5}$ ，则AC的长为（）

A、3 $\sqrt{2}$ B、4 $\sqrt{2}$ C、5 $\sqrt{2}$ D、 $\frac{5}{2} \sqrt{2}$

查看试题解析

二、多选题

10. 下列运算错误的是（）

A、 $\sqrt{5} - \sqrt{3} = \sqrt{2}$ B、 $\sqrt{4 \frac{1}{9}} = 2 \frac{1}{3}$ C、 $\sqrt{8} - \sqrt{2} = \sqrt{2}$ D、 $\sqrt{{(2 - \sqrt{5})}^{2}} = 2 - \sqrt{5}$

查看试题解析

三、填空题

11. 在实数范围内分解因式 $a^{2} - 3$ ＝．

查看试题解析
12. 已知a、b、c是△ABC三边的长，且满足关系式 $\sqrt{c^{2} - a^{2} - b^{2}} + | a - b | = 0$ ，
则△ABC的形状为

查看试题解析
13. 如图，把两块相同的含30°角的三角尺如图放置，若 $A D = 6 \sqrt{6}$ cm，则三角尺的最长边长为．

查看试题解析
14. 观察下面几组勾股数，并寻找规律：
①4，3，5；
②6，8，10；
③8，15，17；
④10，24，26；
请你根据规律写出第⑤组勾股数是．

查看试题解析
15. 在△ABC中，E、F、G、H分别为AC、CD、 BD、 AB的中点，若AD=3，BC=8，则四边形EFGH的周长是．

查看试题解析
16. 勾股定理是几何中的一个重要定理．在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入矩形内得到的，∠BAC=90°，AB=3，AC=4，点D，E，F，G，H，I都在矩形KLMJ的边上，则矩形KLMJ的面积为．

查看试题解析
17. 如图，在平面直角坐标系中有一边长为1的正方形OABC，边OA，OC分别在x轴，y轴上，如果以对角线OB为边作第二个正方形 $O B B_{1} C_{1}$ ，再以对角线 $O B_{1}$ 为边作第三个正方形 $O B_{1} B_{2} C_{2}$ ，照此规律作下去，则点 $B_{2020}$ 的坐标为 .

查看试题解析

四、解答题

18. 计算：

(1)、 $\sqrt{24} + \sqrt{\frac{2}{3}} - 3 \sqrt{6}$

(2)、 $\sqrt{\frac{2}{3}} \div \sqrt{2 \frac{2}{3}} \times \sqrt{\frac{2}{5}}$

(3)、 $(\sqrt{3} - 2)^{2013} \cdot (2 + \sqrt{3})^{2014} - 2 | - \frac{\sqrt{3}}{2} | - (- \sqrt{3})^{0}$

(4)、 $(\sqrt{48} - 4 \sqrt{\frac{1}{8}}) - (3 \sqrt{\frac{1}{3}} - 2 \sqrt{0.5})$

(5)、先化简，再求值： $(\frac{3 x + 4}{x^{2} - 1} - \frac{2}{x - 1}) \div \frac{x^{2} + 2 x}{x^{2} - 1}$ ，其中 $x = \sqrt{2}$ ．

查看试题解析
19. 已知：如图，四边形ABCD，AB=1，BC=2，CD=2，AD=3，且AB⊥BC．求四边形ABCD的面积．

查看试题解析
20. 如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD，等边△ABE．已知∠BAC=30°，EF⊥AB，垂足为F，连接DF．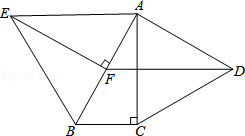

(1)、试说明AC=EF；

(2)、求证：四边形ADFE是平行四边形．

查看试题解析
21.
“为了安全，请勿超速”，如图所示是一条已经建成并通车的公路，且该公路的某直线路段MN上限速17m/s，为了检测来往车辆是否超速，交警在MN旁设立了观测点C．若某次从观测点C测得一汽车从点A到达点B行驶了5秒钟，已知∠CAN=45°，∠CBN=60°，BC=200m．

(1)、求观测点C到公路MN的距离；

(2)、请你判断该汽车是否超速？（参考数据： $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73）

查看试题解析
22. 在解决数学问题时，我们一般先仔细阅读题干，找出有用信息作为已知条件，然后利用这些信息解决问题，但是有的题目信息比较明显，我们把这样的信息称为显性条件；而有的信息不太明显，需要结合图形，特殊式子成立的条件，实际问题等发现隐含信息作为条件，我们把这样的条件称为隐含条件；所以我们在做题时，要注意发现题目中的隐含条件．
阅读下面的解题过程，体会如何发现隐含条件并回答下面的问题．

(1)、按照下面的解法，试化简： $\sqrt{(x - 3)^{2}}$ -（ $\sqrt{2 - x}$ ）² ．
化简：（ $\sqrt{(1 - 3 x)}$ ）²-|1-x|
解：隐含条件1-3x≥0
解得x≤ $\frac{1}{3}$ ∴1-x＞0
∴原式＝（1-3x）-（1-x）
＝1-3x-1+x
＝-2x

(2)、实数a，b在数轴上的位置如图所示，化简 $\sqrt{a^{2}} + {\sqrt{(a + b)}}^{2}$ -|b-a|；

(3)、已知a，b，c为△ABC的三边长，化简：
$\sqrt{{(a + b + c)}^{2}} + {\sqrt{(a - b - c)}}^{2} + {\sqrt{(b - a - c)}}^{2} + \sqrt{{(c - b - a)}^{2}}$

查看试题解析
23. 阅读下列材料，完成相应的任务：有人说，解几何题“得辅助线者得天下”．这句话虽然有些夸张，但是学好添加辅助线是我们快速解题的重要途径．如遇条件中有中点，中线、中位线等，那么过中点，延长中线或中位线作辅助线，使延长的某一段等于中线或中位线；另一种辅助线是过中点作已知边或线段的平行线，以达到应用某个定理或造成全等的目的．
小明在学完做辅助线的方法后，是这样解这个题目的．
如图所示，在四边形ABCD中，AB=CD=6，M、N分别是AD、BC的中点，∠ABD=20°，∠BDC=140°，求MN的长．
解：取BD的中点P，连接PM、PN
∵M、N、P分别是AD、BC、BD的中点，∴PM $∥$ AB，PM = $\frac{1}{2}$ AB，PN $∥$ CD，PN = $\frac{1}{2}$ CD
∵AB=CD=6
∴PM=PN =3
∵PM $∥$ AB，PN $∥$ CD，
∴∠MPD=∠ABD=20°，∠BPN=∠BDC=140°，
∴∠DPN=40°，
∴∠MPN=∠MPD+∠DPN=60°，
∴△MPN是等边三角形，∴MN=PM=6
请你仿照小明的解题思路，完成下列各题．
如图，在四边形ABCD中，E，F分别是AD，BC的中点．

(1)、若AB=6，CD=8，∠ABD=30°，∠BDC=120°，求EF的长；

(2)、若∠BDC-∠ABD=90°，求证：AB²+CD²=4EF² ．

查看试题解析
24. 如图，平行四边形OABC的顶点O为坐标原点，A点在x轴正半轴上，∠COA=60°，OA=10cm，OC=4cm，点P从C点出发沿CB方向，以1cm/s的速度向点B运动；点Q从A点同时出发沿AO方向，以3cm/s的速度向原点运动，其中一个动点达到终点时，另一个动点也随之停止运动．

(1)、求点C，B的坐标（结果用根号表示）

(2)、从运动开始，经过多少时间，四边形OCPQ是平行四边形；

查看试题解析
25. 如图，平行四边形OABC的顶点O为坐标原点，A点在x轴正半轴上，∠COA=60°，OA=10cm，OC=4cm，点P从C点出发沿CB方向，以1cm/s的速度向点B运动；点Q从A点同时出发沿AO方向，以3cm/s的速度向原点运动，其中一个动点达到终点时，另一个动点也随之停止运动．

(1)、求点C，B的坐标（结果用根号表示）

(2)、从运动开始，经过多少时间，四边形OCPQ是平行四边形

(3)、在点P，Q运动的过程中，四边形OCPQ有可能成为直角梯形吗？若能，求出运动时间；若不能，请说明理由；

(4)、在点P、Q运动过程中，四边形OCPQ有可能成为菱形吗？若能，求出运动时间；若不能，请说明理由．（提示：四条边都相等的四边形是菱形）

查看试题解析