山东省济宁市金乡县2021-2022学年八年级下学期6月月考数学试题
试卷更新日期:2023-01-13 类型:月考试卷
一、单选题
-
1. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、3 D、43. 如图,直线l上有三个正方形a,b,c,若a,c的面积分别为3和4,则b的面积为( )
 A、3 B、4 C、5 D、74. 直角三角形的两条直角边的长分别为5,12,则斜边上的高线的长为( )A、cm B、13cm C、cm D、cm5. 已知正比例函数 , y随x的增大而减小,那么一次函数的图象大致是如图中的( ).A、
A、3 B、4 C、5 D、74. 直角三角形的两条直角边的长分别为5,12,则斜边上的高线的长为( )A、cm B、13cm C、cm D、cm5. 已知正比例函数 , y随x的增大而减小,那么一次函数的图象大致是如图中的( ).A、 B、
B、 C、
C、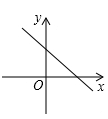 D、
D、 6. 如图,正方形的边长为8,在上,且 , 是上一动点,则的最小值为( )
6. 如图,正方形的边长为8,在上,且 , 是上一动点,则的最小值为( ) A、6 B、8 C、10 D、127. 如图,函数与的图象相交于点 , 则关于x的不等式的解集( )
A、6 B、8 C、10 D、127. 如图,函数与的图象相交于点 , 则关于x的不等式的解集( ) A、 B、 C、 D、8. 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
A、 B、 C、 D、8. 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )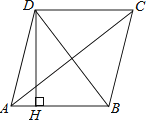 A、 B、 C、12 D、249. 如图,四边形为菱形, , 两点的坐标分别是 , , , 点 , 在坐标轴上,则菱形的周长等于( )
A、 B、 C、12 D、249. 如图,四边形为菱形, , 两点的坐标分别是 , , , 点 , 在坐标轴上,则菱形的周长等于( ) A、8 B、4 C、6 D、510. 一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15km/h,水流速度为5km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是( )A、
A、8 B、4 C、6 D、510. 一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15km/h,水流速度为5km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是( )A、 B、
B、 C、
C、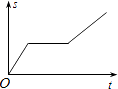 D、
D、
二、填空题
-
11. 若 在实数范围内有意义,则实数x的取值范围是.12. 已知 、 、 是△ABC三边的长,且满足关系式 ,则△ABC的形状为13. 图所示的正方形网格内,点A,B,C,D,E是网格线交点,那么 ° .
 14. 一次函数的图象过点 , 且y随x的增大而增大,则m= .15. 如图,在△ABC 中,AB=AC=12,BC=8, BE 是高,且点 D、F 分别是边 AB、BC 的中点,则△DEF 的周长等于 .
14. 一次函数的图象过点 , 且y随x的增大而增大,则m= .15. 如图,在△ABC 中,AB=AC=12,BC=8, BE 是高,且点 D、F 分别是边 AB、BC 的中点,则△DEF 的周长等于 .
三、解答题
-
16. 计算:17. 已知:如图,四边形ABCD中,AB=BC=2,CD=1,DA=3,∠ABC=90°,求四边形ABCD的面积.
 18. 如图,在 的正方形网格中,按 的形状要求,分别找出格点C,且使 ,并且直接写出对应三角形的面积.
18. 如图,在 的正方形网格中,按 的形状要求,分别找出格点C,且使 ,并且直接写出对应三角形的面积.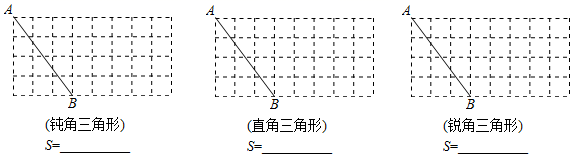 19. 如图,平行四边形 中,点 , 分别在边 , 上, , .
19. 如图,平行四边形 中,点 , 分别在边 , 上, , . (1)、求证:四边形 是矩形;(2)、连接 , 若 , , 平分 , 求 的长.20. 如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,满足∠EAO=∠DCO.
(1)、求证:四边形 是矩形;(2)、连接 , 若 , , 平分 , 求 的长.20. 如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,满足∠EAO=∠DCO. (1)、求证:四边形AECD是平行四边形;(2)、若AB=BC,CD=5,AC=8,求四边形AECD的面积.21. 平面直角坐标系xOy中,已知点A(0,3)、点B(3,0),一次函数y=2x的图象与直线AB交于点M.
(1)、求证:四边形AECD是平行四边形;(2)、若AB=BC,CD=5,AC=8,求四边形AECD的面积.21. 平面直角坐标系xOy中,已知点A(0,3)、点B(3,0),一次函数y=2x的图象与直线AB交于点M.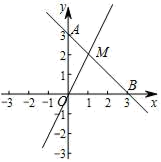 (1)、求直线AB的函数解析式及M点的坐标;(2)、若点N是x轴上一点,且△MNB的面积为6,求点N的坐标.22. 在平面直角坐标系xOy中,如果点A,点C为某个菱形的一组对角的顶点,且点A,C在直线y=x上,那么称该菱形为点A,C的“极好菱形”.如图为点A,C的“极好菱形”的一个示意图.已知点M的坐标为(1,1),点P的坐标为(3,3).
(1)、求直线AB的函数解析式及M点的坐标;(2)、若点N是x轴上一点,且△MNB的面积为6,求点N的坐标.22. 在平面直角坐标系xOy中,如果点A,点C为某个菱形的一组对角的顶点,且点A,C在直线y=x上,那么称该菱形为点A,C的“极好菱形”.如图为点A,C的“极好菱形”的一个示意图.已知点M的坐标为(1,1),点P的坐标为(3,3).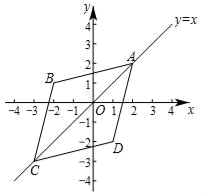 (1)、点E(2,1),F(1,3),G(4,0)中,能够成为点M,P的“极好菱形”的顶点的是;(2)、如果四边形MNPQ是点M,P的“极好菱形”.
(1)、点E(2,1),F(1,3),G(4,0)中,能够成为点M,P的“极好菱形”的顶点的是;(2)、如果四边形MNPQ是点M,P的“极好菱形”.①当点N的坐标为(3,1)时,求四边形MNPQ的面积;
②当四边形MNPQ的面积为8,且与直线y=x+b有公共点时,写出b的取值范围.