辽宁省营口市协作校2020-2021学年八年级下学期第三次质检数学试题

试卷更新日期：2023-01-13 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列二次根式中，属于最简二次根式的是（）

A、 $\sqrt{2}$ B、 $\sqrt{\frac{3}{5}}$ C、 $\sqrt{24}$ D、 $\sqrt{0.5}$

查看试题解析
2. 下列对于二次根式的计算正确的是（）

A、 $\sqrt{3} + \sqrt{3} = \sqrt{6}$ B、2 $\sqrt{3} - \sqrt{3}$ ＝2 C、2 $\sqrt{3} \div \sqrt{3}$ ＝2 D、2 $\sqrt{3} \times \sqrt{3}$ ＝ $\sqrt{18}$

查看试题解析
3. 若代数式 $\frac{\sqrt{x + 2}}{x}$ 有意义，则实数x的取值范围是（）

A、 $x > - 2$ 且 $x \neq 0$ B、 $x \neq 0$ C、 $x \geq - 2$ D、 $x \geq - 2$ 且 $x \neq 0$

查看试题解析
4. 若平行四边形中两个相邻内角度数比为1：2，则其中较大的内角是（）

A、90° B、60° C、120° D、45°

查看试题解析
5. 如图，长方形OABC的边OA长为2，AB长为1，OA在数轴上，以原点O为圆心，对角线OB的长为半径画弧，交正半轴于一点，则这个点表示的实数是（）.

A、2.5 B、 $\sqrt{3}$ C、 $\sqrt{5}$ D、3

查看试题解析
6. 如图，正方形ABCD的面积是（）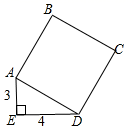

A、5 B、25 C、7 D、1

查看试题解析
7. 如图，在 $▱ A B C D$ 中，AB＝4，BC＝7，∠ABC的平分线交AD于点E，则ED等于（）

A、2 B、3 C、4 D、5

查看试题解析
8. 直线 $y = 3 x + 1$ 向下平移2个单位，所得直线的解析式是（）

A、 $y = 3 x + 3$ B、 $y = 3 x - 2$ C、 $y = 3 x + 2$ D、 $y = 3 x - 1$

查看试题解析
9. 如图，直线 $y_{1} = k_{1} x + a$ 与 $y_{2} = k_{2} x + b$ 的交点坐标为 $(4 ， 8)$ ，则使 $y_{1} < y_{2}$ 的 $x$ 的取值范围为（）

A、 $x > 4$ B、 $x > 8$ C、 $x < 4$ D、 $x < 8$

查看试题解析
10. 在正方形ABCD中，P为AB的中点，BE⊥PD的延长线于点E，连接AE、BE、FA⊥AE交DP于点F，连接BF，FC．下列结论：①△ABE≌△ADF；②FB＝AB；③CF⊥DP；④FC＝EF，其中正确的是（）

A、①②④ B、①③④ C、①②③ D、①②③④

查看试题解析

二、填空题

11. 计算： $3 \sqrt{3} + 2 \sqrt{3}$ 的结果是.

查看试题解析
12. 如图，已知函数y=ax+b和y=kx的图象交于点P，根据图象可得，二元一次方程组 ${\begin{array}{l} y = a x + b \\ y = k x \end{array}$ 的解是．

查看试题解析
13. 如图，在正方形ABCD中，AB＝9，点E在CD边上，且DE＝2CE，点P是对角线AC上的一个动点，则PE+PD的最小值是．

查看试题解析
14. 如图，某斜拉桥的主梁AD垂直于桥面MN于点D，主梁上两根拉索AB、AC长分别为13米、20米，主梁AD的高度为12米，则固定点B、C之间的距离为米.

查看试题解析
15. 若点 $A (2 ， a)$ 、 $B (- 1 ， b)$ 在直线y=-x+1上，则a、b的大小关系是ab.（填“>”“=”或“<”）

查看试题解析
16. 已知一次函数y₁＝kx＋b与y₂＝x＋a的图象如图所示，则下列结论：①k＜0；②a＞0；③b＜0；④关于x的方程kx＋b＝x＋a的解为x＝3；⑤x＞3时，y₁＜y₂ ，其中正确的结论是．（只填序号）

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{24} \div \sqrt{\frac{1}{2}} - (\sqrt{6} + \sqrt{2})^{2} + (π - \sqrt{3})^{0}$ ；

(2)、 $(7 + 4 \sqrt{3}) (2 - \sqrt{3})^{2} - (2 + \sqrt{3}) (2 - \sqrt{3}) + \sqrt{3}$ ．

查看试题解析
18. 先化简，再求值． $\frac{x^{2} - 1}{x}$ ÷（1- $\frac{2 x - 1}{x}$ ），其中x＝ $\sqrt{2}$ ．

查看试题解析
19. 已知一次函数的图象过点（1，-1），（-1，2）．

(1)、求这个函数的解析式；

(2)、求当x＝2时的函数值．

查看试题解析
20. 已知直线 $y = 2 x + 3$ 与直线 $y = - 2 x - 1$ 的图象如图所示，

(1)、求两条直线分别与y轴的交点A，B的坐标；

(2)、求两直线交点C的坐标；

(3)、求 $△ A B C$ 的面积．

查看试题解析
21. 已知：如图，在平行四边形ABDC中，点E、F在AD上，且AE=DF，
求证：四边形BECF是平行四边形．

查看试题解析
22. 如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，且AF=DC，连接CF，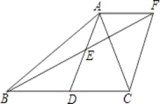

(1)、求证：BD=DC；

(2)、如果AB=AC，试猜测四边形ADCF的形状，并证明你的结论．

查看试题解析
23. 某市的A县和B县春季育苗，急需化肥分别为90t和60t，该市的C县和D县分别储存化肥100t和50t，全部调配给A县和B县．已知从C县运化肥到A县的运费为35元/t，从C县运化肥到B县的运费为30元/t，从D县运化肥到A县的运费为40元/t，从D县运化肥到B县的运费为45元/t．

(1)、设C县运到A县的化肥为xt，求总运费W（单位：元）关于x（单位：t）的函数解析式，并写出自变量x的取值范围；

(2)、求最低总运费，并说明总运费最低时的运送方案．

查看试题解析
24. 在边长为1的正方形ABCD中，点E是射线BC上一动点，AE与BD相交于点M，AE或其延长线与DC或其延长线相交于点F，G是EF的中点，连结CG．

(1)、如图1，当点E在BC边上时．求证：①△ABM≌△CBM；②CG⊥CM.

(2)、如图2，当点E在BC的延长线上时，（1）中的结论②是否成立？请写出结论，不用证明．

(3)、试问当点E运动到什么位置时，△MCE是等腰三角形?请说明理由.

查看试题解析
25. 在坐标平面中，直线y＝x+5分别交x轴、y轴于A、B，直线y＝-2x+20分别交x轴、y轴于C、D，直线AB、CD相交于E，

(1)、求点E的坐标；

(2)、点P为线段AE上的一点，过点P作x轴的平行线分别交直线CB、CD于F、G，设P点的横坐标为m，线段PF的长度为d，求d与m的函数关系式（直接写出自变量m的取值范围）；

(3)、在（2）的条件下，当直线EF把△BCD的面积分成2：3两部分时，求m的值．

查看试题解析