辽宁省大连市高新园区名校联盟2021-2022学年八年级下学期4月月考数学试题
试卷更新日期:2023-01-13 类型:月考试卷
一、单选题
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 下列各组数中,以它们为边长的线段能构成直角三角形的是( )A、1,2,3 B、1, , C、4,5,6 D、12,15,203. 下列运算正确的是( )A、 B、 C、 D、4. 如图,在△ABC中,∠C=90°,AC=4,BC=3,以AB为边作正方形ABDE,则正方形ABDE的面积为( )
 A、5 B、9 C、16 D、255. 下列各式中,与是同类二次根式的是( )A、 B、 C、 D、6. 在一个直角三角形中,若斜边的长是13,一条直角边的长为5,那么这个直角三角形的面积是( )A、30 B、40 C、50 D、607. 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )
A、5 B、9 C、16 D、255. 下列各式中,与是同类二次根式的是( )A、 B、 C、 D、6. 在一个直角三角形中,若斜边的长是13,一条直角边的长为5,那么这个直角三角形的面积是( )A、30 B、40 C、50 D、607. 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( ) A、90° B、60° C、45° D、30°8. 已知实数a在数轴上的对应点位置如图所示,则化简 的结果是( )
A、90° B、60° C、45° D、30°8. 已知实数a在数轴上的对应点位置如图所示,则化简 的结果是( )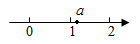 A、 B、-1 C、1 D、9. 如图,在平面直角坐标系中,点的坐标分别为 , 以点A为圆心,以长为半径画弧交x轴上点C,则点C的坐标为( )
A、 B、-1 C、1 D、9. 如图,在平面直角坐标系中,点的坐标分别为 , 以点A为圆心,以长为半径画弧交x轴上点C,则点C的坐标为( ) A、 B、 C、 D、或10. 下列命题:①全等三角形的对应角相等;②一个正数的绝对值等于本身;③若三角形的三边长、、满足 , 则该三角形是直角三角形;④等边三角形的三个内角都等于 . 其中逆命题是真命题的是( )A、 B、 C、 D、
A、 B、 C、 D、或10. 下列命题:①全等三角形的对应角相等;②一个正数的绝对值等于本身;③若三角形的三边长、、满足 , 则该三角形是直角三角形;④等边三角形的三个内角都等于 . 其中逆命题是真命题的是( )A、 B、 C、 D、二、填空题
-
11. 若式子 有意义,则实数 的取值范围是.12. 在△ABC中,∠C=90°, , 则= .13. 已知长方形的面积为12,共中一边长为 ,则该长方形的另一边长为 .14. 在《九章算术》中有一个问题(如图):今有竹高一丈,末折抵地,去本三尺,问折者高几何?它的意思是:一根竹子原高一丈( 尺),中部一处折断,竹梢触地面处离竹根 尺,试问折断处离地面尺.
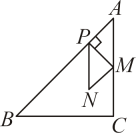
 15. 已知 , , 则 .16. 如图,在中, , , , 点在上,按图中所示方法将沿折叠,使点落在边上的点处,则折痕的长为.
15. 已知 , , 则 .16. 如图,在中, , , , 点在上,按图中所示方法将沿折叠,使点落在边上的点处,则折痕的长为.
三、解答题
-
17. 计算:(1)、;(2)、 .18. 已知x=-1,求代数式(3+2)x2+(+1)x+的值.19. 如图,在中,于点 , , , 求与的长.
 20. 如图所示,一架25米长的梯子AC斜靠在一面竖直的墙AB上,这时梯子底端C到墙的距离BC为7米.
20. 如图所示,一架25米长的梯子AC斜靠在一面竖直的墙AB上,这时梯子底端C到墙的距离BC为7米.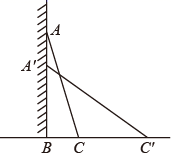 (1)、求这个梯子的顶端距地面的高度AB的长;(2)、如果梯子的顶端A沿墙下滑4米到点 ,小明说梯子的底端C在水平方向向右也滑动4米.你认为小明说的对吗?请说明你的理由.21. 如图,甲乙两船从港口A同时出发,甲船以16海里/时的速度向北偏东40°航行,乙船向南偏东50°航行,小时后,甲船到达C岛,乙船到达B岛,若CB两岛相距17海里,问乙船的航速是多少?
(1)、求这个梯子的顶端距地面的高度AB的长;(2)、如果梯子的顶端A沿墙下滑4米到点 ,小明说梯子的底端C在水平方向向右也滑动4米.你认为小明说的对吗?请说明你的理由.21. 如图,甲乙两船从港口A同时出发,甲船以16海里/时的速度向北偏东40°航行,乙船向南偏东50°航行,小时后,甲船到达C岛,乙船到达B岛,若CB两岛相距17海里,问乙船的航速是多少? 22. 阅读材料:黑白双雄、纵横江湖;双剑合璧、天下无敌.这是武侠小说中的常见描述,其意是指两个人合在一起,取长补短,威力无比.在二次根式中也有这种相辅相成的“对子”如: , , 它们的积不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样理解:如 , , 像这样,通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.
22. 阅读材料:黑白双雄、纵横江湖;双剑合璧、天下无敌.这是武侠小说中的常见描述,其意是指两个人合在一起,取长补短,威力无比.在二次根式中也有这种相辅相成的“对子”如: , , 它们的积不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样理解:如 , , 像这样,通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.解决问题:
(1)、的有理化因式可以是 , 分母有理化得 .(2)、计算:① .
②已知: , , 求的值.
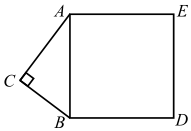
23. 在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G. (1)、求证:∠AEB=∠ACF;(2)、求证:EF2+BF2=2AC2 .24. 阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如 , 善于思考的小明进行了以下探索:
(1)、求证:∠AEB=∠ACF;(2)、求证:EF2+BF2=2AC2 .24. 阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如 , 善于思考的小明进行了以下探索:设(其中a、b、m、n均为正整数),则有 ,
∴a=m2+2n2 , b=2mn.
这样小明就找到了一种把部分的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)、当a、b、m、n均为正整数时,若 , 用含m、n的式子分别表示a、b,得:a= , b=;(2)、若 , 且a、m、n均为正整数,求a的值;(3)、化简: .