江西省赣州市经济开发区2021-2022学年八年级下学期第五次练习数学试题

试卷更新日期：2023-01-13 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列各数中是无理数的是（）

A、3.14 B、 $\frac{22}{7}$ C、 $\sqrt{9}$ D、 $\sqrt{2022}$

查看试题解析
2. 在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，已知a：b=5：12，c=26，则△ABC的面积为（）

A、96 B、98 C、108 D、120

查看试题解析
3. 下列各式计算正确的是（）

A、 $\sqrt[3]{- 1}$ ＝-1 B、 $\sqrt[3]{8}$ ＝±2 C、 $\sqrt{4}$ ＝±2 D、 $\sqrt{(- 3)^{2}}$ ＝-3

查看试题解析
4. 在△ABC中，∠B＝35°，BC²-AC²＝AB² ，则∠C的大小为（）

A、35° B、55° C、65° D、90°

查看试题解析
5. 若x²＝3，则x＝ $\sqrt{3}$ ，若x³＝3，则x＝ $\sqrt[3]{3}$ ，若要使x＝± ${}_{2020}{\sqrt{3}}$ ，则需满足（）

A、x²⁰²⁰＝±3 B、x²⁰²⁰＝3 C、x^±2020＝3 D、x³＝2020

查看试题解析
6. 下列满足条件的三角形中，不是直角三角形的是（）

A、在△ABC中，若a＝ $\frac{3}{5}$ c，b＝ $\frac{4}{5}$ c．则△ABC为直角三角形 B、三边长的平方之比为1：2：3 C、三内角之比为3：4：5 D、三边长分别为a，b，c，c＝1+n² ， b＝n²-1，a＝2n（n＞1）

查看试题解析

二、填空题

7. $\sqrt{9}$ 的平方根是

查看试题解析
8. 比较大小： $\frac{\sqrt{2}}{2}$ $\frac{1}{2}$ （填写“＞”或“＜”或“＝”）.

查看试题解析
9. 一个正数a的两个平方根分别是x+1与x-3，则a的值为．

查看试题解析
10. 如图，在△ABC中，∠C=90°，AC=4，BC=2，以AB为一条边向三角形外部作正方形ABDE，P为DE上一点，则四边形ACBP的面积为．

查看试题解析
11. 《九章算术》勾股卷有一题目：今有垣高一丈.依木于垣，上于垣齐.引木却行四尺，其木至地，问木长几何？意即：一道墙高一丈，一根木棒靠于墙上，木棒上端与墙头齐平，若木棒下端向后退，则木棒上端会随着往下滑，当木棒下端向后退了四尺时，木棒上端恰好落到地上，则木棒长尺(1丈=10尺).

查看试题解析
12. 如图，在Rt△ABC中，∠ACB=90°，AC=2，BC=1，D为射线BC上一点，且△ABD为等腰三角形，则CD的长为．

查看试题解析

三、解答题

13.

(1)、计算： $\sqrt[3]{- 27} + \sqrt{5} (\sqrt{5} - \frac{1}{\sqrt{5}})$

(2)、如图，在△ABC中，AD⊥BC，垂足为点D，AB=13，BD=5，CD=9．求△ABC的面积．

查看试题解析
14. 比较下列算式的结果的大小（填“＞”“＜”或“＝”）．

(1)、4+5 2 $\sqrt{4 \times 5}$
$\frac{1}{2}$ 2 $\sqrt{8 \times \frac{1}{2}}$
5+5 $2 \sqrt{5 \times 5}$

(2)、通过观察归纳，用含字母a，b的式子表示（1）中的规律，并证明．

查看试题解析
15. 图1是放置在水平面上的可折叠式护眼灯，其中底座的高AB=5cm，连杆BC=30cm，灯罩CD=20cm．如图2，转动BC、CD，使得∠BCD成平角，且灯置端点D离桌面l的高度DH为45cm，求AH的距离，

查看试题解析
16. 如图，点A表示的数为- $\sqrt{2}$ ，一只蚂蚁从点A沿数轴向右直爬2个单位后到达点B，设点B所表示的数为n．求|n+1|+（n+2 $\sqrt{2}$ -2）的值．

查看试题解析
17. 如图是5×5的方格纸，每个小正方形的边长为1，顶点为格点，我们把每个顶点都在格点上的三角形称为格点三角形、请仅用无刻度的直尺按以下要求作图：

(1)、在图1中作出面积为5的格点正方形；

(2)、在图2中作出周长为（2 $\sqrt{5} + \sqrt{10}$ ）的格点直角三角形．

查看试题解析
18. 李明刚买了一套毛坯新房，其中一个房间的地板为一个长宽之比为4：3的长方形，其面积为12m² ．

(1)、求这个房间地板的长和宽：

(2)、用48块大小相同的正方形地板砖刚好把这个房间地板铺满，求这种地板砖的边长，

查看试题解析
19. 求值

(1)、已知 $\sqrt[3]{1 - 2 x}$ 与 $\sqrt[3]{3 x - 7}$ 互为相反数，求 $\sqrt{10 x + 4}$ 的值；

(2)、已知 $| 2 a + 6 |$ 与 $\sqrt{3 b + 12}$ 互为相反数，求2a-3b的平方根．

查看试题解析
20. 如图，在△ABC中，AB=4，BC= $\sqrt{5}$ ，点D在AB上，且BD=1，CD=2．

(1)、求证：CD⊥AB；

(2)、求AC的长．

查看试题解析
21. 如图，已知△ABC的三边长分别为a、b、c，且2c-1的算术平方根为5，2b-3立方根为3， $\sqrt[3]{5 - 2 a}$ 与 $\sqrt[3]{3 a - 19}$ 互为相反数．

(1)、分别求a、b、c的值；

(2)、求△ABC的面积．

查看试题解析
22. 如图1，图2分别是某种型号拉杆箱的实物图与示意图，根据商品介绍，获得了如下信息：滑竿DE、箱长BC拉杆AB的长度都相等，即DE=BC=AB=50，点B、F在线段AC上，点C在DE上，支杆DF=30cm．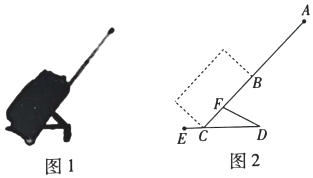

(1)、若EC=36cm时，B，D相距48cm，试判定BD与DE的位置关系，并说明理由；

(2)、当∠DCF＝45°，CF＝ $\frac{1}{5}$ AC时，求CD的长．

查看试题解析
23. 在△ABC中，点P是平面内任意一点（不同于A、B、C），若点P与A、B、C中的某两点的连线的夹角为直角时，则称点P为△ABC的一个勾股点．

(1)、如图1，若点P是△ABC内一点，∠A=55°，∠ABP=10°，∠ACP=25°，试说明点P是△ABC的一个勾股点；

(2)、如图2，已知点D是与A、C两点的连线的夹角为直角，且∠DCB=∠DAC，若AD=3CD=3，BC=6，求AB的长；

(3)、如图3，在Rt△ABC中，∠ACB=90°，AC=12，BC=16，点D在AB上，且AD=BD=CD，点P在射线CD上．若点P是△ABC的勾股点，请求出CP的长．

查看试题解析