吉林省长春汽车经济技术开发区2021-2022学年八年级下学期线上教学质量检测数学试题
试卷更新日期:2023-01-13 类型:月考试卷
一、单选题
-
1. 函数中自变量的取值范围( )A、 B、 C、 D、2. 在平面直角坐标系中,点A(-2022,2022)位于哪个象限?( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 2022年2月20日,北京冬奥会圆满闭幕,冬奥会的部分金牌榜如表所示,榜单上各国代表团获得的金牌数的众数为( )
代表团
挪威
德国
中国
美国
瑞典
荷兰
奥地利
金牌数
16
12
9
8
8
8
7
A、9 B、8.5 C、8 D、74. 在 中,若 ,则 的大小为( )A、80° B、100° C、110° D、160°5. 一次函数的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. “禾下乘凉梦,一稻一人生”,某科研小组在袁隆平精神的引领下,对所培育的甲、乙两块试验田里稻穗的长度抽样调查得出,平均穗长相同,穗长的方差分别为 , , 则穗长更整齐的试验田是( )A、甲 B、乙 C、甲、乙相同 D、无法确定7. 为调查学生对国家“一带一路”倡议的知晓率,某市一所中学初中部准备调查60名学生,以下样本具有代表性的是( )A、全校男生中随机抽取60名 B、七年级学生中随机抽取60名 C、全校共青团员中随机抽取60名 D、七、八、九年级分别随机抽取20名8. 如图,在平面直角坐标系中,点是轴正半轴上的一个定点,点是函数的图象上的一个动点,轴于点 . 当点的纵坐标逐渐增大时,四边形的面积的变化为( ) A、不变 B、逐渐增大 C、逐渐减小 D、先增大后减小
A、不变 B、逐渐增大 C、逐渐减小 D、先增大后减小二、填空题
-
9. 如图,若的周长是 , 的周长是 , 则的长为 .
 10. 一次函数y=(k+5)x﹣2中y随x的增大而减小,则k的取值范围是.11. 为了估计湖里有多少鱼,我们从湖里捕上150条鱼作上标记,然后放回湖里去,经过一段时间再捕上300条鱼,其中带标记的鱼有30条,则估计湖里约有鱼条.12. 如图,E为▱ABCD的边AD上任意一点,▱ABCD的面积为6,则图中阴影部分的面积为 .
10. 一次函数y=(k+5)x﹣2中y随x的增大而减小,则k的取值范围是.11. 为了估计湖里有多少鱼,我们从湖里捕上150条鱼作上标记,然后放回湖里去,经过一段时间再捕上300条鱼,其中带标记的鱼有30条,则估计湖里约有鱼条.12. 如图,E为▱ABCD的边AD上任意一点,▱ABCD的面积为6,则图中阴影部分的面积为 .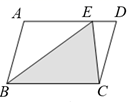 13. 如图,在平行四边形ABCD中,AB=4,BC=5,以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于 PQ的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是 .
13. 如图,在平行四边形ABCD中,AB=4,BC=5,以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于 PQ的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是 .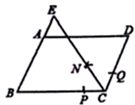 14. 直线与的交点坐标为 , 则使的的取值范围是 .
14. 直线与的交点坐标为 , 则使的的取值范围是 .
三、解答题
-
15. 在平面直角坐标系中,已知点、、的坐标分别为、、 , 点与点关于原点对称.请在平面直角坐标系中描出点、、、的位置.
 16. 已知一次函数的图象过和两点.(1)、求此一次函数的解析式.(2)、若点在这个函数图象上,求的值.17. 已知:如图,平行四边形中, , 交于点 , 于点 , 于点 .
16. 已知一次函数的图象过和两点.(1)、求此一次函数的解析式.(2)、若点在这个函数图象上,求的值.17. 已知:如图,平行四边形中, , 交于点 , 于点 , 于点 .求证: .
 18. 某学校需招聘一名教师,对应聘者的专业知识、语言表达、社会实践三项进行测试,三项测试的满分均为100分.现有、、、四名应聘者的得分情况如下表:
18. 某学校需招聘一名教师,对应聘者的专业知识、语言表达、社会实践三项进行测试,三项测试的满分均为100分.现有、、、四名应聘者的得分情况如下表:应聘者
测试项目成绩(分)
专业知识
语言表达
社会实践
80
70
90
90
55
80
80
75
70
80
85
80
(1)、应聘者三项测试成绩的平均分为分.(2)、根据工作需要,学校将三项测试分数依次按的比例计入每人的总分,再按得分最高的录用,那么谁将被录用?19. 如图都是 的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,在每个正方形网格中标注了6个格点,这6个格点简称为标注点. (1)、请在如图1,如图2中,以4个标注点为顶点,各画一个平行四边形(两个平行四边形不全等).(2)、如图1中所画的平行四边形的面积为.20. 运动是健康的源泉.为了解学生身体健康状况,某学校对学生进行立定跳远水平测试,并随机抽取50名学生的成绩(单位:m)进行整理,绘制成如下不完整的频数分布表和频数分布直方图.
(1)、请在如图1,如图2中,以4个标注点为顶点,各画一个平行四边形(两个平行四边形不全等).(2)、如图1中所画的平行四边形的面积为.20. 运动是健康的源泉.为了解学生身体健康状况,某学校对学生进行立定跳远水平测试,并随机抽取50名学生的成绩(单位:m)进行整理,绘制成如下不完整的频数分布表和频数分布直方图.学生立定跳远测试成绩的频数分布表
分组
成绩
频数
第一组
第二组
12
第三组
第四组
10
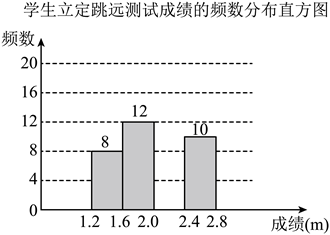
请根据图表中所提供的信息,完成下列问题:
(1)、表中a= , b= .(2)、样本成绩的中位数落在第组范围内.(3)、请将频数分布直方图补充完整.(4)、已知该校共有1000名学生,估计该校学生立定跳远成绩在范围内的约有人.21. 甲、乙两地相距480千米,一辆货车和一辆轿车先后从甲地出发驶向乙地(两车速度均保持不变).如图,折线表示轿车离甲地的距离(千米)与时间(小时)之间的函数关系,线段表示货车离甲地的距离(千米)与时间(小时)之间的函数关系,请根据图像信息,解答下列问题: (1)、货车的速度是千米/时,a= .(2)、求线段对应的函数表达式.(3)、直接写出轿车从甲地出发后经过多长时间追上货车及追上时两车离乙地的距离.22. 【教材呈现】下图是华师版八年级下册数学教材第83页和84页的部分内容.
(1)、货车的速度是千米/时,a= .(2)、求线段对应的函数表达式.(3)、直接写出轿车从甲地出发后经过多长时间追上货车及追上时两车离乙地的距离.22. 【教材呈现】下图是华师版八年级下册数学教材第83页和84页的部分内容.平行四边形的判定定理2 一组对边平行且相等的四边形是平行四边形.
我们可以用演绎推理证明这一结论.
已知:如图,在四边形中,ABCD且 .
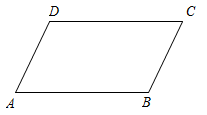
求证:四边形是平行四边形.
证明:连接 .
(1)、请根据教材提示,结合图,写出完整的证明过程.(2)、【知识应用】如图①,在中,延长到点 , 使 , 连接、 . 求证:四边形是平行四边形.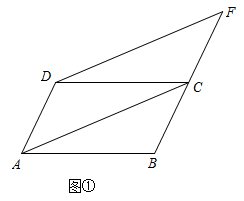 (3)、【拓展提升】在【知识应用】的条件下,若四边形的面积为7,直接写出四边形的面积.23. 如图,点是函数图像上的任意一点,过点作ABx轴,交另一个函数的图像于点 .
(3)、【拓展提升】在【知识应用】的条件下,若四边形的面积为7,直接写出四边形的面积.23. 如图,点是函数图像上的任意一点,过点作ABx轴,交另一个函数的图像于点 . (1)、若 , 则k= .(2)、当时,若点的横坐标是1,则线段 .(3)、若无论点在何处,函数图像上总存在一点 , 使得四边形为平行四边形,求的值.24. 如图,在四边形中,ADBC, , , , , 动点从点出发,沿射线以每秒3个单位的速度运动,动点同时从点出发,在线段上以每秒1个单位的速度向终点运动,当动点到达点时,动点也同时停止运动.设点的运动时间为(秒).
(1)、若 , 则k= .(2)、当时,若点的横坐标是1,则线段 .(3)、若无论点在何处,函数图像上总存在一点 , 使得四边形为平行四边形,求的值.24. 如图,在四边形中,ADBC, , , , , 动点从点出发,沿射线以每秒3个单位的速度运动,动点同时从点出发,在线段上以每秒1个单位的速度向终点运动,当动点到达点时,动点也同时停止运动.设点的运动时间为(秒). (1)、线段的长为 .(2)、用含的代数式表示线段的长.(3)、求当为何值时,以点、、、为顶点的四边形是平行四边形?(4)、直接写出以线段为腰,为等腰三角形时的值.
(1)、线段的长为 .(2)、用含的代数式表示线段的长.(3)、求当为何值时,以点、、、为顶点的四边形是平行四边形?(4)、直接写出以线段为腰,为等腰三角形时的值.