吉林省名校调研2021-2022学年八年级下学期5月月考数学试题

试卷更新日期：2023-01-13 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $\sqrt{2^{2}} = 2$ B、 $\sqrt{9} = \pm 3$ C、 $\sqrt{12} = 6$ D、 $\sqrt{\frac{1}{6}} = \sqrt{6}$

查看试题解析
2. 下列各组数不能作为直角三角形的三边长的是（）

A、8，15，17 B、7，12，15 C、5，12，13 D、7，24，25

查看试题解析
3. 在平面直角坐标系中，点 $P (- 1 ， 2)$ 到原点的距离是（）

A、1 B、2 C、 $\sqrt{3}$ D、 $\sqrt{5}$

查看试题解析
4. 若将直线 $y = - x$ 向下平移2个单位长度，则平移后所得直线对应的函数解析式为（）

A、 $y = - x + 2$ B、 $y = - x - 2$ C、y=-x+1 D、 $y = - x - 1$

查看试题解析
5. 若一次函数 $y = k x + b (k \neq 0)$ 的图象如图所示，则不等式 $k x + b < 0$ 的解集为（）

A、 $x < 3$ B、 $x > 3$ C、 $x < 4$ D、 $x > 4$

查看试题解析
6. 如图，两张等宽的纸条交叉重叠在一起，重叠的部分为四边形ABCD，若测得A，C之间的距离为12cm，点B，D之间的距离为16m，则线段AB的长为（）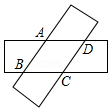

A、9.6cm B、10cm C、20cm D、12cm

查看试题解析

二、填空题

7. 在函数y= $\sqrt{5 - x}$ 中，自变量x的取值范围是．

查看试题解析
8. 若一个直角三角形的斜边长是4，一条直角边的长是1，则它的第三条边的长是．

查看试题解析
9. 若正比例函数 $y = (m - 1) x$ 的图象从左到右逐渐上升，则m的取值范围是．

查看试题解析
10. 某种型号汽车的油箱容量为40L，每行驶100km耗油10L．设一辆加满油的该型号汽车行驶的路程为 $x (k m)$ ，行驶过程中油箱内剩余的油量为y（L），则y与x之间的函数关系式是．

查看试题解析
11. 如图，E是 $▱ A B C D$ 内部一点，连接 $A E$ 、 $B E$ 、 $C E$ 、 $D E$ ．若图中阴影部分的面积是2，则 $▱ A B C D$ 的面积是．

查看试题解析
12. 如图，小华将升旗的绳子拉到竖直旗杆底端，绳子末端刚好接触到地面，然后将绳子末端拉到距离旗杆 $8 m$ 处，此时绳子末端距离地面 $2 m$ ，则绳子的长度为 $m$ ．

查看试题解析
13. 我们知道，四边形具有不稳定性．如图，在平面直角坐标系中，边长为2的正方形ABCD的边AB在x轴上，AB的中点是坐标原点O，固定点A，B，把正方形沿箭头方向推，使点D落在y轴正半轴上点D'处，则点C的对应点C'的坐标为．

查看试题解析
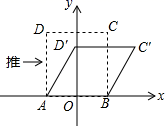14. 在平面直角坐标系中，过一点分别作坐标轴的垂线，若与坐标轴围成的矩形的周长与面积相等，则称这个点为强点．例如：如图，过点 $B (3 ， 6)$ 分别作x轴、y轴的垂线，与坐标轴围成的矩形 $O A B C$ 的周长与面积相等，则点B是强点．若强点 $M (a ， 3)$ 在第一象限，且在直线 $y = - x + b$ （b为常数）上，则b的值为．

查看试题解析

三、解答题

15. 计算： $\sqrt{12} - \sqrt{27} + \sqrt{\frac{1}{3}}$ ．

查看试题解析
16. 如图，在 $▱ A B C D$ 中、 $A E$ 平分 $∠ B A D$ 交 $B C$ 边于点E．若 $A D = 4$ ， $A B = 3$ ，求 $C E$ 的长．

查看试题解析
17. 如图，在平面直角坐标系中，直线 $y = k x + b (k \neq 0)$ 与直线 $y = x$ 交于点 $A (2 ， a)$ ，与y轴交于点 $B (0 ， 6)$ ．求直线 $y = k x + b$ 对应的函数解析式．

查看试题解析
18. 已知 $y - 5$ 与 $x + 3$ 成正比例，且当 $x = 1$ 时， $y = - 3$ ．

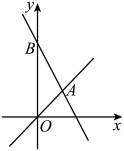(1)、写出y与x之间的函数关系式；

(2)、求当 $x = - 7$ 时，y的值．

查看试题解析
19. 如图，在 $4 \times 4$ 的正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫做格点．线段 $A B$ 、 $C D$ 、 $E F$ 的顶点都在格点上．

(1)、分别写出图中线段 $A B$ 、 $C D$ 、 $E F$ 的长；

(2)、证明以线段 $A B$ 、 $C D$ 、 $E F$ 为三边的三角形是直角三角形．

查看试题解析
20. 如图，在△ABC中，AB=AC，点D在BC上，已知BD=CD，点E是AB的中点，过点A作AF∥BC，交DE延长线于点F，连接AD，BF，求证：四边形AFBD是矩形．

查看试题解析
21. 已知一次函数 $y = (m - 2) x + 3 - m$ 的图象不经过第三象限，且m为正整数．

(1)、求m的值；

(2)、当 $- 4 < y < 0$ 时，求x的取值范围．

查看试题解析
22. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 3$ ， $B C = 4$ ．以 $△ A B C$ 的三边为边向 $A B$ 同侧分别作正方形 $A B M N$ 、正方形 $A C D E$ 和正方形 $B C F G$ ，点M在边 $F G$ 上， $M N$ 交 $C F$ 于点P， $A N$ 交 $C D$ 于点Q．

(1)、求证： $△ A B Q ≌ △ N A P$ ；

(2)、求四边形 $C P N Q$ 的面积．

查看试题解析
23. 某工地需要利用炸药实施爆破，操作人员点燃导火线后，要在炸药爆炸前跑到300米以外的安全区域，炸药导火线的长度y（厘米）与燃烧的时间x（秒）之间的函数关系如图所示.

(1)、请写出点B的实际意义，

(2)、求y与x之间的函数关系式，并写出自变量的取值范围.

(3)、问操作人员跑步的速度必须超过多少，才能保证安全.

查看试题解析
24. 【操作】如图①，在矩形 $A B C D$ 中，E为对角线 $A C$ 上的一点（不与点A重合）．将 $△ A D E$ 沿射线 $A B$ 方向平移到 $△ B C F$ 的位置，点E的对应点为点F，易证： $△ A D E ≌ △ B C F$ （不需要证明）；
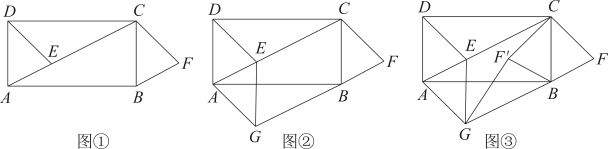
【探究】过图①的点E作 $E G ∥ B C$ ，交 $F B$ 的延长线于点G，连接 $A G$ ，其他条件不变，如图②．求证： $△ E G A ≌ △ B C F$ ；
【拓展】将图②中的 $△ B C F$ 沿 $B C$ 翻折得到 $△ B C F^{'}$ ，连接 $G F^{'}$ ，其他条件不变，如图③．当 $G F^{'}$ 最短时，若 $A B = 4$ ， $B C = 2$ ，直接写出四边形 $B F C F^{'}$ 的周长．

查看试题解析
25. 甲、乙两辆汽车先后从A地出发到B地，甲车出发1小时后，乙车才出发，如图所示的 $l_{1}$ 和 $l_{2}$ 分别表示甲、乙两车相对于出发地的距离y（km）与追赶时间x（h）之间的函数关系图象．

(1)、甲、乙两车的速度分别是多少？

(2)、分别确定甲、乙两车相对于出发地的距离y（km）与追赶时间x（h）之间的函数关系式；

(3)、乙车能在它出发1.5小时内追上甲车吗？若能，说明理由；若不能，求乙车出发几小时才能追上甲车？

查看试题解析
26. 如图，在矩形 $A B C D$ 中， $A B = 2$ ， $B C = 6$ ，等腰直角三角形 $P Q M$ 的顶点P在边 $B C$ 上，点B、C、M在同一直线上， $∠ Q = 90 °$ ， $M P = 6$ ． $△ P Q M$ 从点B出发，以每秒1个单位长度的速度沿边 $B C$ 向右平移，当点C与点P重合时停止运动．设 $△ P Q M$ 与矩形 $A B C D$ 重叠部分图形的面积为S（平方单位），平移的时间为t（秒）．

(1)、当点A在 $△ P Q M$ 的边上时，求 $t$ 的值；

(2)、求S与 $t$ 之间的函数关系式；

(3)、当 $△ P Q M$ 与矩形 $A B C D$ 重叠部分的图形是轴对称图形时，直接写出t的取值范围．

查看试题解析