河北省石家庄市赵县2021-2022学年八年级下学期3月月考数学试题

试卷更新日期：2023-01-13 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列各式一定是二次根式的是（）

A、 $\sqrt{- 3}$ B、 $\sqrt{3 m}$ C、 $\sqrt{a^{2} + 1}$ D、 $\sqrt[3]{5}$

查看试题解析
2. 不论a为何值，下列式子一定有意义的是（）

A、 $\sqrt{a}$ B、 $\sqrt{- a}$ C、 $\sqrt{\frac{1}{a}}$ D、 $\sqrt{a^{2} + 2}$

查看试题解析
3. 下列式子中，最简二次根式的是（）

A、 $\sqrt{9}$ B、 $\sqrt{7}$ C、 $\sqrt{12}$ D、 $\sqrt{\frac{1}{3}}$

查看试题解析
4. 下列二次根式中能与2 $\sqrt{3}$ 合并的是（）

A、 $\sqrt{8}$ B、 $\sqrt{\frac{1}{3}}$ C、 $\sqrt{18}$ D、 $\sqrt{9}$

查看试题解析
5. 若 $\sqrt{75 n}$ 是整数，则正整数n的最小值是（）

A、2 B、3 C、4 D、5

查看试题解析
6. 下列等式正确的是（）

A、（ $\sqrt{3}$ ）²=3 B、 $\sqrt{{(- 3)}^{2}}$ =﹣3 C、 $\sqrt{3^{3}}$ =3 D、（﹣ $\sqrt{3}$ ）²=﹣3

查看试题解析
7. 如果最简二次根式 $\sqrt{3 a - 8}$ 与 $\sqrt{17 - 2 a}$ 能够合并，那么 $a$ 的值为（）.

A、2 B、3 C、4 D、5

查看试题解析
8. 下列计算 $\sqrt{18}$ ﹣ $\sqrt{2}$ 的结果是（）

A、4 B、3 C、2 $\sqrt{2}$ D、 $\sqrt{2}$

查看试题解析
9. 计算并化简 $\sqrt{5} \times \sqrt{\frac{4}{5}}$ 的结果为（）

A、2 B、 $\sqrt{4}$ C、±2 D、 $\pm \sqrt{4}$

查看试题解析
10. 若 $x y < 0$ ，则 $\sqrt{x^{2} y}$ 化简后为（）

A、 $- x \sqrt{y}$ B、 $x \sqrt{y}$ C、 $x \sqrt{- y}$ D、 $- x \sqrt{- y}$

查看试题解析
11. ${(\sqrt{10} + 3)}^{2020} {(\sqrt{10} - 3)}^{2019}$ 的结果是（）

A、 $\sqrt{10} - 3$ B、3 C、-3 D、 $\sqrt{10} + 3$

查看试题解析
12. 如果 $\sqrt{x} • \sqrt{x - 6} = \sqrt{x (x - 6)}$ ，那么（）

A、 $x \geq 0$ B、 $x \geq 6$ C、 $0 \leq x \leq 6$ D、x为一切实数

查看试题解析
13. 下列运算正确的是（）

A、 $\sqrt{2}$ + $\sqrt{3}$ = $\sqrt{5}$ B、 $\sqrt{18}$ =2 $\sqrt{3}$ C、 $\sqrt{2}$ • $\sqrt{3}$ = $\sqrt{5}$ D、 $\sqrt{2}$ ÷ $\sqrt{\frac{1}{2}}$ =2

查看试题解析
14. 下列各式正确的是（）

A、 $(\sqrt{2} + \sqrt{5}) \times \sqrt{7} = \sqrt{7} \times \sqrt{7} = 7$ B、 $(\sqrt{5} + \sqrt{3}) (\sqrt{5} - \sqrt{2}) = 5 - \sqrt{6}$ C、 $(\sqrt{3} - \sqrt{2}) (\sqrt{3} + \sqrt{2}) = 3 - 2 = 1$ D、 ${(\sqrt{5} - \sqrt{3})}^{2} = 5 - 3 = 2$

查看试题解析
15.
实数a，b在数轴上对应点的位置如图所示，化简|a|+ $\sqrt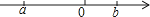{{(a - b)}^{2}}$ 的结果是（　　）

A、﹣2a+b B、2a﹣b C、﹣b D、b

查看试题解析
16. 对于任意的正数m，n定义运算※为：m※n＝ ${\begin{matrix} \sqrt{m} - \sqrt{n} (m \geq n) \\ \sqrt{m} + \sqrt{n} (m < n) \end{matrix}$ 计算(3※2)×(8※12)的结果为（）

A、2－4 $\sqrt{6}$ B、2 C、2 $\sqrt{5}$ D、20

查看试题解析

二、填空题

17. 计算 $(\sqrt{3} + \sqrt{2}) - \sqrt{3}$ 的结果是

查看试题解析
18. $\sqrt{10} \div \sqrt{2} =$ ．

查看试题解析
19. 观察下列式子： $\sqrt{9 \times 9 + 19} = 10 ， \sqrt{99 \times 99 + 199} = 100$ ，则 $\sqrt{999 \times 999 + 1999} =$ ， …， $\sqrt{99999 \times 99999 + 199999} =$ ；根据以上式子的规律计算： $\sqrt{\underset{n 个 9}{\underset{︸}{9999 \cdot \cdot \cdot 9}} × \underset{n 个 9}{\underset{︸}{9999 \cdot \cdot \cdot 9}} + \underset{n 个 9}{\underset{︸}{199 \cdot \cdot \cdot 9}}} =$ ．

查看试题解析

三、解答题

20. 已知 $\sqrt{a - 5}$ + $\sqrt{5 - a}$ =b+3

(1)、求a的值；

(2)、求a²﹣b²的平方根.

查看试题解析
21. 化简：

(1)、 $\frac{1}{2} \sqrt{\frac{4}{7}}$

(2)、 $\sqrt{202 - 152}$

(3)、 $\sqrt{\frac{32 \times 9}{25}}$

(4)、 $\sqrt{20.5}$

查看试题解析
22. 计算：

(1)、 $\sqrt{48} \div \sqrt{3} - \sqrt{\frac{1}{2}} \times \sqrt{12} + \sqrt{24}$

(2)、 $(3 \sqrt{18} + \frac{1}{5} \sqrt{50} - 4 \sqrt{\frac{1}{2}}) \div \sqrt{32}$

(3)、 $(5 + \sqrt{6}) (5 \sqrt{2} - 2 \sqrt{3})$

查看试题解析
23. 如图所示，数轴上表示1， $\sqrt{2}$ 的对应点分别为A，B，沿过点A的直线折叠，点B落在数轴上点C处，设点C所表示的数为x，求x的值．

查看试题解析
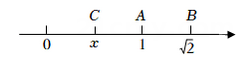24. 观察下列等式：
① $\frac{1}{\sqrt{2} + 1} = \frac{\sqrt{2} - 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$ ；
② $\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ；
③ $\frac{1}{\sqrt{4} + \sqrt{3}} = \frac{\sqrt{4} - \sqrt{3}}{(\sqrt{4} + \sqrt{3}) (\sqrt{4} - \sqrt{3})} = \sqrt{4} - \sqrt{3}$ ；…
回答下列问题：

(1)、利用你观察到的规律，化简： $\frac{1}{\sqrt{5} + \sqrt{4}} =$ ；

(2)、计算： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \frac{1}{\sqrt{5} + \sqrt{4}}$ ；

(3)、计算： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + ⋯ + \frac{1}{\sqrt{n} + \sqrt{n - 1}}$ ．

查看试题解析
25. 在一个边长为（ $\sqrt{3} + \sqrt{5}$ ）cm的正方形内部挖去一个边长为（ $\sqrt{5} - \sqrt{3}$ ）cm的正方形（如图所示），求剩余阴影部分图形的面积．

查看试题解析
26. 阅读材料：小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如： $3 + 2 \sqrt{2} = （ 1 + \sqrt{2} ）^{2}$ ，善于思考的小明进行了以下探索：
设 $a + b \sqrt{2} = {(m + n \sqrt{2})}^{2}$ （其中 $a 、 b 、 m 、 n$ 均为整数），则有 $a + b \sqrt{2} = m^{2} + {2n}^{2} + 2mn \sqrt{2}$ ．

∴ $a = m^{2} + {2n}^{2} ， b = 2mn$ ．这样小明就找到了一种把部分 $a + b \sqrt{2}$ 的式子化为平方式的方法．

请你仿照小明的方法探索并解决下列问题：

(1)、当 $a 、 b 、 m 、 n$ 均为正整数时，若 $a + b \sqrt{3} = {(m + n \sqrt{3})}^{2}$ ，用含m、n的式子分别表示 $a 、 b$ ，得 $a$ ＝， $b$ ＝；

(2)、利用所探索的结论，找一组正整数 $a 、 b 、 m 、 n$ ，填空：＋＝（＋ $\sqrt{3}$ ）²；

(3)、若 $a + 4 \sqrt{3} = {(m ＋ n \sqrt{3})}^{2}$ ，且 $a 、 b 、 m 、 n$ 均为正整数，求 $a$ 的值．

查看试题解析