广东省深圳市宝安区2021-2022学年八年级下学期数学第一阶段综合练习题

试卷更新日期：2023-01-13 类型：月考试卷

进入出卷网下载

一、单选题

1. 通过平移图中的吉祥物“海宝”得到的图形是（）

A、 B、 C、 D、

查看试题解析
2. 如图，∠C＝∠D＝90°，若添加一个条件，可使用“HL”判定Rt△ABC与Rt△ABD全等，则以下给出的条件适合的是（）

A、AC＝AD B、AB＝AB C、∠ABC＝∠ABD D、∠BAC＝∠BAD

查看试题解析
3. 已知等腰三角形的其中两边长分别为4，9，则这个等腰三角形的周长是（）

A、13 B、17 C、22 D、17或22

查看试题解析
4. 如图，四边形ABCD中，AC垂直平分BD，垂足为E，下列结论不一定成立的是（）

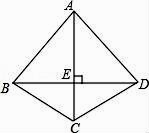A、AB=AD B、AC平分∠BCD C、AB=BD D、△BEC≌△DEC

查看试题解析
5. 如图，将△ABC沿射线BC的方向移动，使点B移动到点C，得到△DCE，连接AE.若△ABC的面积为2，则△ACE的面积为（）

A、2 B、4 C、8 D、16

查看试题解析
6. 下列命题中，逆命题正确的是（）

A、对顶角相等 B、两直线平行，同位角相等 C、全等三角形对应角相等 D、等腰三角形是轴对称图形

查看试题解析
7. 如图，在△ABC中，∠CAB=75°，在同一平面内，将△ABC绕点A旋转到△AB'C’的位置，使得CC' $∥$ AB，则∠BAB'= （）

A、30° B、35° C、40° D、50°

查看试题解析
8. 如图，△ABC中，∠C=90°，AC=3，∠B=30°，点P是BC边上的动点，则AP的长不可能是（）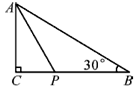

A、3.5 B、4.2 C、5.8 D、7

查看试题解析
9. 如图，O是△ABC内一点，且O到三边AB、BC、CA的距离OF＝OD＝OE，若∠BAC＝70°，则∠BOC的度数为（）

A、70° B、120° C、125° D、130°

查看试题解析
10. 如图，在△ABC中，AB边的中垂线DE，分别与AB、AC边交于点D、E两点，BC边的中垂线FG，分别与BC、AC边交于点F、G两点，连接BE、BG．若△BEG的周长为16，GE＝1．则AC的长为（）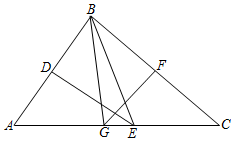

A、13 B、14 C、15 D、16

查看试题解析

二、填空题

11. 将点P（2，1）沿x轴方向向左平移3个单位，再沿y轴方向向上平移2个单位，所得的点的坐标是.

查看试题解析
12. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 5 c m$ ， $B C = 12 c m$ ，则内部五个小直角三角形的周长的和为．

查看试题解析
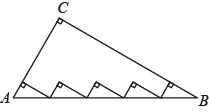13. 如图，在△ABC中，∠C＝90°，∠B＝22.5°，DE垂直平分AB交BC于点E，EC＝2，则△ACE的面积为．

查看试题解析
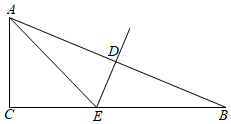14. 如图，在由边长为1的小正方形组成的5×5的网格中，点A，B在小方格的顶点上，要在小方格的顶点确定一点C，连接AC和BC，使△ABC是等腰三角形．则方格图中满足条件的点C的个数有个．

查看试题解析
15. 如图，已知在 $△ A B C$ 中， $A B = 4 ， B C = 5 ， ∠ A B C = 60 °$ ，在边 $A C$ 上方作等边 $△ A C D$ ，则 $B D$ 的长为．

查看试题解析

三、解答题

16. 在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系，△ABC的顶点都在格点上，请解答下列问题：
⑴作出△ABC向左平移4个单位长度后得到的△A₁B₁C₁ ，并写出点C₁的坐标；
⑵将△A₁B₁C₁绕原点O逆时针旋转90°得到△A₂B₂C₂ ，请画出旋转后的△A₂B₂C₂ ，并写出点C₂的坐标．

查看试题解析
17. 如图，在△ABC中，AB＝AC，点D是BA延长线上的一点，点E是AC的中点．

(1)、实践与操作：利用尺规按下列要求作图，并在图中标明相应字母：（保留作图痕迹，不写作法）
①作∠DAC的平分线AM；
②连接BE并延长交AM于点F；

(2)、求证： $A F ∥ B C$ 且AF＝BC．

查看试题解析
18. 如图，在等腰Rt△ABC中，∠A＝90°，AB＝AC，点D是斜边BC的中点，点E、F分别为AB、AC边上的点，且DE⊥DF．

(1)、判断DF与DE的大小关系，并说明理由；

(2)、若BE＝8，CF＝6，求：
①EF的长；
②△DEF的面积．

查看试题解析
19. 如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C＝90°，∠B＝∠E＝30°．

(1)、晓晓在操作中发现：如图2，固定△ABC，使△DEC绕点C顺时针旋转．当点D恰好落在AB边上时，填空：
①线段DE与AC的位置关系是；
②设△BDC的面积为S₁ ， △AEC的面积为S₂ ，则S₁与S₂的数量关系是；

(2)、猜想论证：当△DEC绕点C旋转到图3所示的位置时，晓晓猜想（1）中S₁与S₂的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC，CE边上的高，请你证明晓晓的猜想．

查看试题解析
20. 把正方形纸片放在直角坐标系中，如图所示，正方形纸片ABCD的边长为3，点E、F分别在BC、CD上，将AB、AD分别沿AE、AF折叠，点B、D恰好都落在点G处，已知3BE＝BC．

(1)、请直接写出D、E两点的坐标，并求出直线EF的解析式；

(2)、在直线EF上是否存在点M，使得△AFM的面积是△AEF的面积的一半，若存在，请求出点M的坐标，若不存在，请说明理由．

(3)、若点P、Q分别是线段AG、AF上的动点，则EP＋PQ的最小值是多少？并求出此时点Q的坐标．

查看试题解析