广东省深圳市2021-2022学年八年级下学期2月月考数学试题

试卷更新日期：2023-01-13 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列式子：①3＞0；②4x+3y＞0；③x=3；④x-1≠5；⑤x+2≤3 是不等式的有（）

A、2 个 B、3 个 C、4 个 D、5 个

查看试题解析
2. 已知一个等腰三角形的两边长分别是2和4，则该等腰三角形的周长为（　　）

A、8或10 B、8 C、10 D、6或12

查看试题解析
3. 不等式 $- 2 x < 6$ 的非正整数解有（）

A、1个 B、2个 C、3个 D、无数多个

查看试题解析
4. 具备下列条件的△ABC中，不是直角三角形的是（）

A、 $a ： b ： c = 1 ： 1 ： \sqrt{2}$ B、∠A+∠B=∠C C、∠A：∠B：∠C=3：2：1 D、 $a^{2} ： b^{2} ： c^{2} = 5 ： 12 ： 13$

查看试题解析
5. 到三角形三边的距离相等的点是三角形（）的交点

A、三条中线 B、三条高线 C、三个内角平分线 D、三边垂直平分线

查看试题解析
6. 以下命题中，属于真命题的是（）．

A、同位角相等 B、两边和一角对应相等的两个三角形全等 C、面积相等的两个三角形全等 D、等腰三角形底边中点到两腰的距离相等

查看试题解析
7. 某种衬衫的进价为400元，出售时标价为550元，由于换季，商店准备打折销售，但要保持利润不低于10%，那么至多打（　　）

A、6折 B、7折 C、8折 D、9折

查看试题解析
8. 若 $a < b$ ，那么下列各式中错误的是（）

A、 $a - 1 < b - 1$ B、 $- a < - b$ C、 $2017 a < 2017 b$ D、 $\frac{a}{2014} < \frac{b}{2014}$

查看试题解析
9. 若干学生分宿舍，每间4人余20人，每间8人有一间不空也不满，则宿舍有( )

A、5间 B、6间 C、7间 D、8间

查看试题解析
10. 在△ABC中，∠C=90°，∠BAC和∠ABC的平分线相交于点P，且PE⊥AB于点E．若BC=3，AC=4，则PE的长为（）

A、1 B、2 C、3 D、4

查看试题解析
11. 已知不等式组 ${\begin{matrix} x - 3 (x - 2) < a \\ \frac{1 + 2 x}{3} > x - 1 \end{matrix}$ 仅有2个整数解，那么a的取值范围是（）

A、a≥2 B、a＜4 C、2≤a＜4 D、2＜a≤4

查看试题解析
12. 如图，在△ABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于点D，DE⊥AB，垂足为E，且AB= $3 \sqrt{2}$ ，则△DEB的周长为（）

A、9 B、 $3 \sqrt{2}$ C、 $6 \sqrt{2}$ D、10

查看试题解析

二、填空题

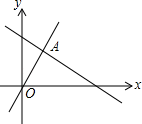
13. 不等式组 ${\begin{array}{l} x \leq 1 \\ x + 3 > 1 \end{array}$ 的所有整数解的和是．

查看试题解析
14. 如图，函数y＝2x和y＝ax+4的图象相交于点A（m，3），则不等式2x≥ax+4的解集为.

查看试题解析
15.
如图，Rt△ABC中，∠B=90°，AB=4，BC=3，AC的垂直平分线DE分别交AB，AC于D，E两点，则CD的长为．

查看试题解析
16. 已知△ABC中，∠A =100°，角平分线BE、CF交于点O，则∠BOC = ．

查看试题解析
17. 如果关于x的不等式组 ${\begin{array}{l} x > a + 2 \\ x < 3 a - 2 \end{array}$ 无解，则常数a的取值范围是．

查看试题解析
18. 如图，在△ABC中，∠BAC=90°，AB=3，AC=4，AD平分∠BAC交BC于D，则BD的长为．

查看试题解析

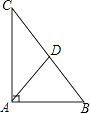
三、解答题

19. 解不等式组： ${\begin{array}{l} 5 x - 1 ＜ 3 (x + 1) \\ \frac{2 x - 1}{3} - \frac{5 x + 1}{2} \leq 1 \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
20. 当负整数m为何值时，关于x的方程 $\frac{5 x - 3 m}{4} = \frac{m}{2} + \frac{15}{4}$ 的解是非负数．

查看试题解析
21. 五一节快到了，甲、乙两家旅行社为了吸引更多的顾客，分别提出了赴某地旅游的团体优惠方法，甲旅行社的优惠方法是：买4张全票，其余人按半价优惠；乙旅行社的优惠方法是：一律按7折优惠，已知两家旅行社的原价均为每人100元．

(1)、分别表示出甲旅行社收费y₁和乙旅行社收费y₂与旅游人数x的函数关系式；

(2)、某单位有8至18人参加旅游（含8人和18人），问哪家旅行社的收费更优惠？

查看试题解析
22.
如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE．
求证：

(1)、△AEF≌△CEB；

(2)、AF=2CD．

查看试题解析
23. 深圳某校6名教师和234名学生外出参加集体活动，学校准备租用45座大车和30座小车若干辆．已知租用1辆大车、2辆小车的租车费用是1000元，租用2辆大车、1辆小车的租车费用是1100元．

(1)、求大、小客车每辆的租车费各是多少元？

(2)、学校要求每辆车上至少要有一名教师，且租车总费用不超过2300元，请问有几种符合条件的租车方案？

查看试题解析
24. 为建设京西绿色走廊，改善永定河水质，某治污公司决定购买10台污水处理设备．现有A、B两种型号的设备，其中每台的价格与月处理污水量如下表：

A型
B型
价格（万元台）
$x$
$y$
处理污水量（吨月）
240
200

(1)、经调查：购买一台A型设备比购买一台B型设备多2万元，购买2台A型设备比购买3台B型设备少6万元．求x、y的值；

(2)、如果治污公司购买污水处理设备的资金不超过105万元，求该治污公司有哪几种购买方案；

(3)、在（2）的条件下，如果月处理污水量不低于2040吨，为了节约资金，请为该公司设计一种最省钱的购买方案．

查看试题解析

	A型	B型
价格（万元台）	$x$	$y$
处理污水量（吨月）	240	200