初中数学同步训练必刷题（北师大版七年级下册1.6 完全平方公式）

试卷更新日期：2023-01-13 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 计算： ${(x + 2 y)}^{2} =$ （）

A、 $x^{2} + 4 x y + 4 y^{2}$ B、 $x^{2} + 2 x y + 4 y^{2}$ C、 $x^{2} + 4 x y + 2 y^{2}$ D、 $x^{2} + 4 x^{2}$

查看试题解析
2. 已知 ${(3 x + a)}^{2} = 9 x^{2} + b x + 4$ ，则b的值为（）

A、4 B、 $\pm 6$ C、12 D、 $\pm 12$

查看试题解析
3. 将 $9 7^{2}$ 变形正确的是（）

A、 $9 7^{2} = 9 0^{2} + 7^{2}$ B、 $9 7^{2} = (100 + 3) (100 - 3)$ C、 $9 7^{2} = 10 0^{2} - 2 \times 100 \times 3 + 3^{2}$ D、 $9 7^{2} = 9 0^{2} + 90 \times 7 + 7^{2}$

查看试题解析
4. 对于等式 $(2 x + □)^{2} = 4 x^{2} + 12 x y + △$ 中，△代表的是（）

A、3y B、9y C、 $9 y^{2}$ D、 $36 y^{2}$

查看试题解析
5. 设 $a = \sqrt{7} - 1$ ，则 $3 a^{3} + 12 a^{2} - 6 a - 12 =$ （）

A、24 B、25 C、 $4 \sqrt{7} + 10$ D、 $4 \sqrt{7} + 12$

查看试题解析
6. 已知 $a - b = 5$ ，且 $c - b = 10$ ，则 $a^{2} + b^{2} + c^{2} - ab - bc - ac$ 等于（）

A、105 B、100 C、75 D、50

查看试题解析
7. 若 $a$ 的值使得 $x^{2} + 4 x + a = {(x + 2)}^{2} - 1$ 成立，则 $a$ 的值为（）

A、5 B、4 C、3 D、2

查看试题解析
8. 若 $x = 1 - \sqrt{2022}$ ，则代数式 $x^{2} - 2 x + 1$ 的值是（）

A、2021 B、2022 C、－2021 D、－2022

查看试题解析
9. 已知 $x + \frac{1}{x} = 8$ ，则 $x^{2} + \frac{1}{x^{2}}$ 的值是（）

A、 $66$ B、 $64$ C、62 D、60

查看试题解析
10. 小明将一个大的正方形剪成如图所示的四个图形(两个正方形、两个长方形)，并发现该过程可以用一个等式来表示，则该等式可以是（）

A、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ B、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ C、 $(a - b) = a^{2} - b^{2}$ D、 ${(a + b)}^{2} = {(a - b)}^{2} + a b$

查看试题解析

二、填空题（每题3分，共30分）

11. 化简： $(a + 1)^{2} =$ ．

查看试题解析
12. 已知 $a + b = 5 ， a b = 3$ ，则 ${(a - b)}^{2}$ 的值是.

查看试题解析
13. 计算： ${(2 a - b + 3 c)}^{2} =$ ．

查看试题解析
14. 如果4x²﹣mxy+9y²是一个完全平方式，则m= ．

查看试题解析
15. 若 $x^{2} - 4 x + a = (x - 2)^{2} - 1$ 成立，则 $a$ 的值为．

查看试题解析
16. 计算： $29 5^{2} + 10 \times 295 + 5^{2} =$

查看试题解析
17. 如果 $(2 x + 5)^{2} = 4 x^{2} + 2 k x + 25$ ，那么 $k$ 的值是．

查看试题解析
18. 当 $a = \sqrt{2021} + 1$ 时，代数式a²﹣2a+2的值是．

查看试题解析
19. 计算 $(a - b) (a + b) (a^{2} + b^{2}) (a^{4} - b^{4})$ 的结果是．

查看试题解析
20. 如图是一个正方形，分成四部分，其面积分别为 $a^{2}$ ， $a b$ ， $a b$ ， $b^{2}$ ，则原正方形的边长是．

查看试题解析

三、解答题（共6题，共60分）

21. 要求：利用乘法公式计算

(1)、 $2023 \times 2021 - 202 2^{2}$

(2)、 $(2 x - y + 3) (2 x - y - 3)$

查看试题解析
22. 先化简，再求值： $(2 x + 5) (2 x - 5) + {(x - 3)}^{2} - 6 x (x - 1)$ ，其中 $x = 6$ .

查看试题解析
23. 将多项式 $9 x^{2} + x$ 加上一个整式后，使它能成为另一个整式的平方，你有哪些方法，请写出三类不同的解法.

查看试题解析
24. 阅读：已知a - b＝ -4，ab＝3，求a²+b²的值．小明的解法如下：
解：因为a - b＝ -4，ab＝3，
所以a² +b²＝（a - b）²+ 2ab＝（- 4）²+ 2×3＝22．
请你根据上述解题思路解答下面问题：
已知a - b＝ -5，ab＝2，求a²+ b²- ab的值．

查看试题解析
25. 完全平方公式： ${(a \pm b)}^{2} = a^{2} \pm 2 a b + b^{2}$ ，适当的变形，可以解决很多的数学问题.例如：若 $a + b = 3$ ， $a b = 1$ ，求 $a^{2} + b^{2}$ 的值.
解：因为 $a + b = 3$ ，
所以 ${(a + b)}^{2} = 0$ ，即： $a^{2} + 2 a b + b^{2} = 9$ ，又因为 $a b = 1$
所以 $a^{2} + b^{2} = 7$
根据上面的解题思路与方法，解决下列问题：

(1)、若 $x + y = 8$ ， $x^{2} + y^{2} = 40$ ，求 $x y$ 的值；

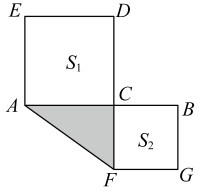(2)、若 $(4 - x) (x - 5) = - 8$ ，求 ${(4 - x)}^{2} + {(x - 5)}^{2}$ 的值；

(3)、如图，点C是线段 $A B$ 上的一点，以 $A C$ 、 $B C$ 为边向两边作正方形，设 $A B = 6$ ，两正方形的面积和 $S_{1} + S_{2} = 18$ ，求图中阴影部分面积.

查看试题解析
26. 把几个图形拼成一个新的图形，再通过两种不同的方法计算同一个图形的面积，可以得到一个等式，也可以求出一些不规则图形的面积.
例如，由图①，可得等式：（a+2b）（a+b）＝a²+3ab+2b².

(1)、如图②，将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形，试用不同的形式表示这个大正方形的面积，你能发现什么结论？请用等式表示出来.

(2)、利用（1）中所得到的结论，解决下面的问题：
已知a+b+c＝10，a²+b²+c²＝38，求ab+bc+ac的值.

(3)、如图③，将两个边长分别为a和b的正方形拼在一起，B，C，G三点在同一条直线上，连结BD和BF.若这两个正方形的边长满足a+b＝10，ab＝20，请求出阴影部分的面积.

查看试题解析