广东省佛山市教研联盟2021-2022学年八年级5月堂上练习数学试题
试卷更新日期:2023-01-13 类型:月考试卷
一、单选题
-
1. 下列式子: , , , , , 其中分式有( )A、1个 B、2个 C、3个 D、4个2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若 ,则下列各式正确的是( )A、 B、 C、 D、4. 如图,中, , , 于, , 的长度是( )
3. 若 ,则下列各式正确的是( )A、 B、 C、 D、4. 如图,中, , , 于, , 的长度是( )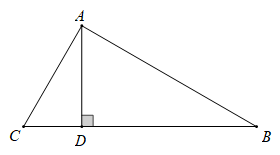 A、 B、 C、 D、无法确定5. 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
A、 B、 C、 D、无法确定5. 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( ) A、30° B、40° C、50° D、65°6. 下列各式从左到右的变形中,为因式分解的是( )A、x(a﹣b)=ax﹣bx B、x2﹣1+y2=(x﹣1)(x+1)+y2 C、ax+bx+c=x(a+b)+c D、y2﹣1=(y+1)(y﹣1)7. 在把多项式因式分解时,虽然它不符合完全平方公式,但经过变形,可以利用完全平方公式进行分解:原式 , 像这样构造完全平方式的方法称之为“配方法”.用这种方法把多项式因式分解的结果是( )A、 B、 C、 D、8. 如果把分式 中的x和y都扩大5倍,那么分式的值( )A、扩大5倍 B、不变 C、缩小5倍 D、扩大10倍9. 如图,已知正比例函数与一次函数的图象交于点P.下面有四个结论:①k>0;②b>0;③当x>0时,>0;④当x<-2时,kx>-x+b.其中正确的是( )
A、30° B、40° C、50° D、65°6. 下列各式从左到右的变形中,为因式分解的是( )A、x(a﹣b)=ax﹣bx B、x2﹣1+y2=(x﹣1)(x+1)+y2 C、ax+bx+c=x(a+b)+c D、y2﹣1=(y+1)(y﹣1)7. 在把多项式因式分解时,虽然它不符合完全平方公式,但经过变形,可以利用完全平方公式进行分解:原式 , 像这样构造完全平方式的方法称之为“配方法”.用这种方法把多项式因式分解的结果是( )A、 B、 C、 D、8. 如果把分式 中的x和y都扩大5倍,那么分式的值( )A、扩大5倍 B、不变 C、缩小5倍 D、扩大10倍9. 如图,已知正比例函数与一次函数的图象交于点P.下面有四个结论:①k>0;②b>0;③当x>0时,>0;④当x<-2时,kx>-x+b.其中正确的是( )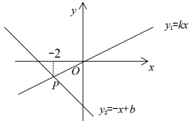 A、①③ B、②③ C、③④ D、①④10. 如图所示,在四边形ABCD中, ,AC=1, ,直线MN为线段AD的垂直平分线,P为MN上的一个动点,则PC+PD的最小值为( )
A、①③ B、②③ C、③④ D、①④10. 如图所示,在四边形ABCD中, ,AC=1, ,直线MN为线段AD的垂直平分线,P为MN上的一个动点,则PC+PD的最小值为( )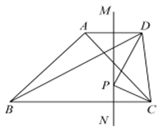 A、1 B、 C、 D、3
A、1 B、 C、 D、3二、填空题
-
11. 当x=时,分式无意义.12. 已知a,b,c为三角形的三边,若有(a+c)2=b2+2ac,则这个三角形的形状是三角形.13. 的公因式是 .14. 化简分式= .15. 如图,将周长为8的沿方向向右平移1.5个单位得到 , 则四边形的周长为 .
 16. 不等式组的解集是 .17. 一直角三角形的一直角边长为6,斜边长比另一直角边长大2,则斜边上的高是 .
16. 不等式组的解集是 .17. 一直角三角形的一直角边长为6,斜边长比另一直角边长大2,则斜边上的高是 .三、解答题
-
18. 计算下列各式(1)、因式分解:;(2)、化简:19. 先化简,再求值: , 其中x=-420. 某校计划购买数学、语文两种书若干本用于图书角建设,已知购买2本数学书和1本语文书需100元:购买6本数学书与购买7本语文书的价格相同.(1)、求数学和语文这两种书的单价:(2)、若购买数学和语文两种书共50本,总价不超过1600元,求这所学校最多购买多少本数学书?21. 在边长为1个单位的小正方形组成的网格中建立如图所示的平面直角坐标系,格点△ABC(顶点是网格线的交点)的顶点坐标分别为 , , .

⑴将△ABC向由右平移3个单位长度,再向上平移4个单位长度得到 , 画出;
⑵①画出绕原点O顺时针旋转90°得到的;
②直接写出的坐标为 ▲ .
22. 如图,已知内部有C、D.两点,要求作一点P使 , 且点P到两边的距离相等,用尺规作图先作 ▲ , 再作 ▲ , 则 ▲ 为所求.(不写作法,保留作图痕迹.) 23. 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(与A、B不重合),连接CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE、BE
23. 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(与A、B不重合),连接CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE、BE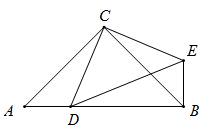 (1)、求证:△ACD≌△BCE;(2)、若BE=5,DE=13,求AB的长24. 下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程.
(1)、求证:△ACD≌△BCE;(2)、若BE=5,DE=13,求AB的长24. 下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程.解:设x2﹣4x=y,
原式=(y+2)(y+6)+4(第一步)=y2+8y+16(第二步)=(y+4)2(第三步)=(x2﹣4x+4)2(第四步)
(1)、该同学第二步到第三步运用了因式分解的_______.A、提取公因式; B、平方差公式; C、两数和的完全平方公式; D、两数差的完全平方公式.(2)、该同学因式分解的结果是否彻底?.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果 .(3)、请你模仿以上方法尝试对多项式(x2+2x)(x2+2x+2)+1进行因式分解.25. 已知:如图1,一次函数y=mx+5m的图像与x轴、y轴分别交于点A、B,与函数y=-x的图像交于点C,点C的横坐标为-3. (1)、求点B的坐标(2)、若点Q为直线OC上一点,且S△QAC=2S△AOC,求点Q的坐标;(3)、如图2,点D为线段OA上一点,∠ACD=∠AOC.点P为x轴负半轴上一点,且点P到直线CD和直线CO的距离相等.
(1)、求点B的坐标(2)、若点Q为直线OC上一点,且S△QAC=2S△AOC,求点Q的坐标;(3)、如图2,点D为线段OA上一点,∠ACD=∠AOC.点P为x轴负半轴上一点,且点P到直线CD和直线CO的距离相等.① 在图2中,只利用圆规作图找到点P的位置; (保留作图痕迹,不得在图2中作无关元素.)
② 求点P的坐标.