广东省佛山市2021-2022学年八年级下学期3月月考数学试题
试卷更新日期:2023-01-13 类型:月考试卷
一、单选题
-
1. 下列选项中的代数式,是分式的为( )A、 B、 C、 D、2. 下列图形中,是中心对称图形的是( )A、
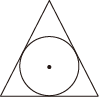 B、
B、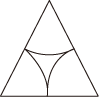 C、
C、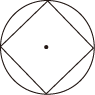 D、
D、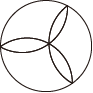 3. 如果 , 那么下列各式中正确的是( )A、 B、 C、 D、4. 已知△ABC中,∠B≠∠C,求证:AB≠AC.若用反证法证这个结论,应首先假设( )A、∠B=∠C B、∠A=∠B C、AB=AC D、∠A=∠C5. 如图,△ABC绕点A逆时针旋转40°得到△ADE,∠BAC=50°,则∠DAC的度数为( )
3. 如果 , 那么下列各式中正确的是( )A、 B、 C、 D、4. 已知△ABC中,∠B≠∠C,求证:AB≠AC.若用反证法证这个结论,应首先假设( )A、∠B=∠C B、∠A=∠B C、AB=AC D、∠A=∠C5. 如图,△ABC绕点A逆时针旋转40°得到△ADE,∠BAC=50°,则∠DAC的度数为( )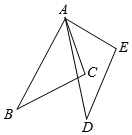 A、10° B、15° C、20° D、25°6. 下列各式是因式分解的是( )A、m2-2m-3=m(m-2)-3 B、6ab=2a•3b C、(x+5)(x-2)=x2+3x-10 D、x2-8x+16=(x-4)27. 下列多项式中,能运用平方差公式分解因式的是A、 B、 C、 D、8. 将分式 中 的值都扩大到原来的3倍,则扩大后分式的值( )A、扩大到原来的3倍 B、扩大到原来的9倍 C、不变 D、缩小到原来的9. 如图,直线y=kx+b与直线y=-交于点A(m,2),则关于x的不等式kx+b x+的解集是( )
A、10° B、15° C、20° D、25°6. 下列各式是因式分解的是( )A、m2-2m-3=m(m-2)-3 B、6ab=2a•3b C、(x+5)(x-2)=x2+3x-10 D、x2-8x+16=(x-4)27. 下列多项式中,能运用平方差公式分解因式的是A、 B、 C、 D、8. 将分式 中 的值都扩大到原来的3倍,则扩大后分式的值( )A、扩大到原来的3倍 B、扩大到原来的9倍 C、不变 D、缩小到原来的9. 如图,直线y=kx+b与直线y=-交于点A(m,2),则关于x的不等式kx+b x+的解集是( )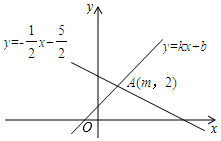 A、x≤2 B、x≥1 C、x≤1 D、x≥210. 已知a,b,c分别是△ABC的三边长,且满足2a4+2b4+c4=2a2c2+2b2c2 , 则△ABC是( )A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形或直角三角形
A、x≤2 B、x≥1 C、x≤1 D、x≥210. 已知a,b,c分别是△ABC的三边长,且满足2a4+2b4+c4=2a2c2+2b2c2 , 则△ABC是( )A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形或直角三角形二、填空题
-
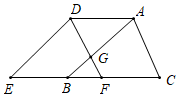
11. 要使分式 有意义,则 的取值范围是 .12. 命题“对顶角相等”的逆命题是一个命题(填“真”或“假”).13. 多项式x3y﹣xy的公因式是.14. 分式化为最简分式的结果是 .15. 如图,将△ABC向左平移3cm得到△DEF,AB、DF交于点G,如果△ABC的周长是12cm,那么△ADG与△BGF的周长之和是 .
 16. 解不等式组 的解集为.17. 已知△ABC为等边三角形,D为边AC上一点,延长BC至E,使CE=CD=1,连接DE,则DE等于 .
16. 解不等式组 的解集为.17. 已知△ABC为等边三角形,D为边AC上一点,延长BC至E,使CE=CD=1,连接DE,则DE等于 .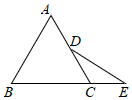
三、解答题
-
18. 计算下列各式.(1)、因式分解:5m3-5m;(2)、化简: .19. 先化简 , 再从-2,2,-1和1中选取一个合适的数做a的值,求原式的值.20. 小颖准备用21元买笔和笔记本.已知每支笔3元,每个笔记本2.5元,她买了2个笔记本.请你帮她算一算,她还可能买几支笔?21. 按要求画图及填空:在由边长为1个单位长度的小正方形组成的网格中建立如图所示平面直角坐标系,原点O及△ABC的顶点都在格点上.
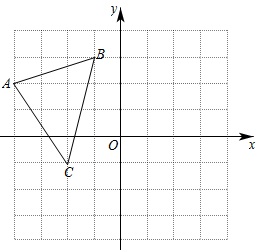
⑴图中线段AB的长度为 ▲ ;
⑵将△ABC先向下平移2个单位长度,再向右平移5个单位长度得到△A1B1C1 , 画出△A1B1C1;
⑶将△ABC绕点B逆时针旋转90°,画出旋转后得到的△A2B2C2 , 直接写出点A2、C2的坐标.
22. 如图,在△ABC中,∠B=30°,∠C=40°.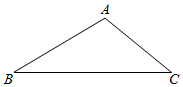 (1)、尺规作图:①作边AB的垂直平分线交BC于点D;
(1)、尺规作图:①作边AB的垂直平分线交BC于点D;②连接AD,作∠CAD的平分线交BC于点E;(要求:保留作图痕迹,不写作法)
(2)、在(1)所作的图中,求∠DAE的度数.23. 如图,点O是等边 内一点,将CO绕点C顺时针旋转 得到CD,连结OD,AO,AD. (1)、求证: .(2)、若 , , ,求 的面积.24. 对于形如x2+2ax+a2这样的二次三项式,可以用公式法将它分解成(x+a)2的形式.但对于二次三项式x2+2ax-3a2 , 就不能直接运用公式了.此时,我们可以在二次三项式x2+2ax-3a2中先加上一项a2 , 使它与x2+2ax的和成为一个完全平方式,再减去a2 , 整个式子的值不变,于是有:x2+2ax-3a2=(x2+2ax+a2)-a2-3a2=(x+a)2-(2a)2=(x+a+2a)(x+a-2a)=(x+3a)(x-a).
(1)、求证: .(2)、若 , , ,求 的面积.24. 对于形如x2+2ax+a2这样的二次三项式,可以用公式法将它分解成(x+a)2的形式.但对于二次三项式x2+2ax-3a2 , 就不能直接运用公式了.此时,我们可以在二次三项式x2+2ax-3a2中先加上一项a2 , 使它与x2+2ax的和成为一个完全平方式,再减去a2 , 整个式子的值不变,于是有:x2+2ax-3a2=(x2+2ax+a2)-a2-3a2=(x+a)2-(2a)2=(x+a+2a)(x+a-2a)=(x+3a)(x-a).像这样,先添一适当项,使式中出现完全平方式,再减去这个项,使整个式子的值不变的方法称为“配方法”.利用“配方法”分解因式:
(1)、n2-6n+8;(2)、x4-3x2y2+y4;(3)、a2-2a-m2-4m-325. 对于平面直角坐标系中的线段及点Q,给出如下定义:若点Q满足 , 则称点Q为线段的“中垂点”;当时,称点Q线段的“完美中垂点”.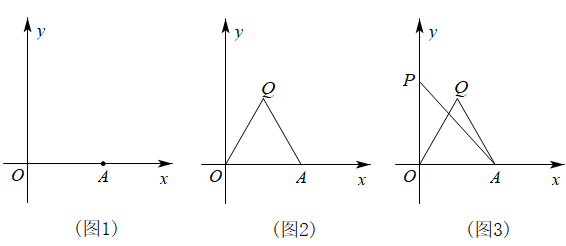 (1)、如图1, , 下列各点中,线段的中垂点是 .(2)、如图2,点A为x轴上一点,若为线段的“完美中垂点”,写出线段的两个“完美中垂点”是和 .(3)、如图3,若点A为x轴正半轴上一点,点Q为线段的“完美中垂点”,点在y轴正半轴上.
(1)、如图1, , 下列各点中,线段的中垂点是 .(2)、如图2,点A为x轴上一点,若为线段的“完美中垂点”,写出线段的两个“完美中垂点”是和 .(3)、如图3,若点A为x轴正半轴上一点,点Q为线段的“完美中垂点”,点在y轴正半轴上.①请用尺规作图在线段上方做出线段的“完美中垂点”M
②求(用含m的式子表示)及 .