安徽省滁州市定远县永康片2021-2022学年八年级下学期第三次教学质量监测数学试题
试卷更新日期:2023-01-13 类型:月考试卷
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 实数a,b在数轴上对应点的位置如图所示,化简|a|+ 的结果是( )
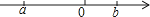 A、﹣2a+b B、2a﹣b C、﹣b D、b3. 已知a<b,化简二次根式 ( )A、 B、 C、 D、4. 若关于x的方程的一个根是 , 则的值为( )A、-1 B、0 C、1 D、25. 如果关于的方程有实数根,那么的取值范围是( )A、 B、且 C、 D、且6. 小匡同学从市场上买一块长80cm、宽70cm的矩形铁皮,准备制作一个工具箱.如图,他将矩形铁皮的四个角各剪掉一个边长xcm的正方形后,剩余的部分刚好能围成一个底面积为3000的无盖长方形工具箱,根据题意列方程为( )
A、﹣2a+b B、2a﹣b C、﹣b D、b3. 已知a<b,化简二次根式 ( )A、 B、 C、 D、4. 若关于x的方程的一个根是 , 则的值为( )A、-1 B、0 C、1 D、25. 如果关于的方程有实数根,那么的取值范围是( )A、 B、且 C、 D、且6. 小匡同学从市场上买一块长80cm、宽70cm的矩形铁皮,准备制作一个工具箱.如图,他将矩形铁皮的四个角各剪掉一个边长xcm的正方形后,剩余的部分刚好能围成一个底面积为3000的无盖长方形工具箱,根据题意列方程为( ) A、 B、 C、 D、7. 如图,AD为等边△ABC边BC上的高,AB=4,AE=1,P为高AD上任意一点,则EP+BP的最小值为( )
A、 B、 C、 D、7. 如图,AD为等边△ABC边BC上的高,AB=4,AE=1,P为高AD上任意一点,则EP+BP的最小值为( ) A、 B、 C、 D、8. 已知a,b,c是 的三边长,且满足 ,则 是( )A、以a为斜边的直角三角形 B、以b为斜边的直角三角形 C、以c为斜边的直角三角形 D、以c为底边的等腰三角形9. 一个多边形的每一个内角都等于 ,那么这个多边形的边数是A、9条 B、8条 C、7条 D、6条10. 如图,平行四边形 的对角线 与 相交于点O, 于点E, , , ,则 的长为( )
A、 B、 C、 D、8. 已知a,b,c是 的三边长,且满足 ,则 是( )A、以a为斜边的直角三角形 B、以b为斜边的直角三角形 C、以c为斜边的直角三角形 D、以c为底边的等腰三角形9. 一个多边形的每一个内角都等于 ,那么这个多边形的边数是A、9条 B、8条 C、7条 D、6条10. 如图,平行四边形 的对角线 与 相交于点O, 于点E, , , ,则 的长为( )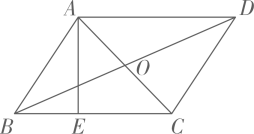 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: .12. 关于x的一元二次方程 有两个不相等的实数根,则 的取值范围是.
13. 如图,△ABC中,AB=13,AD=6,AC=5,D为BC边的中点.则S△ABC= .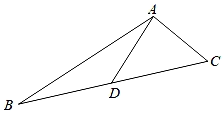 14. 一个多边形的内角和是720°,则这个多边形的对角线共有条.
14. 一个多边形的内角和是720°,则这个多边形的对角线共有条.三、解答题
-
15. 计算:(1)、(2)、先化简,再求值 , 其中 , .16. 观察下列等式,根据其中的规律解决下列问题:
①;②;③;….
(1)、根据规律写出第6个等式;(2)、根据规律用n(n为正整数)表示出第n个等式,并加以证明.17. 已知关于x的一元二次方程 .(1)、若方程的一个根为 ,求a的值;(2)、若方程有实数根,求满足条件的正整数a的值.18. 如图,沿AC方向开山修路.为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=120°,BD=400米,∠D=30°.那么另一边开挖点E离D多远正好使A、C、E三点在一直线上(≈1.732,结果精确到1米)? 19. 已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a,b,c分别为△ABC三边的长.(1)、如果x=-1是方程的根,试判断△ABC的形状,并说明理由;(2)、如果△ABC是等边三角形,试求这个一元二次方程的根.20. 为节省材料,某水产养殖户利用水库堤岸(堤岸足够长)为一边,用总长为120米的围网在水库中围成如图所示的①②③三块矩形区域,且三块区域面积相等.设BC的长度为xm.
19. 已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a,b,c分别为△ABC三边的长.(1)、如果x=-1是方程的根,试判断△ABC的形状,并说明理由;(2)、如果△ABC是等边三角形,试求这个一元二次方程的根.20. 为节省材料,某水产养殖户利用水库堤岸(堤岸足够长)为一边,用总长为120米的围网在水库中围成如图所示的①②③三块矩形区域,且三块区域面积相等.设BC的长度为xm. (1)、求AE的长(用含x的代数式表示).(2)、当矩形ABCD的面积为600m2时,求BC的长.21. 如图,在等腰Rt△ABC中,∠ACB=90°,点D是AB上一点,作等腰Rt△DCE,且∠DCE=90°,连接AE.
(1)、求AE的长(用含x的代数式表示).(2)、当矩形ABCD的面积为600m2时,求BC的长.21. 如图,在等腰Rt△ABC中,∠ACB=90°,点D是AB上一点,作等腰Rt△DCE,且∠DCE=90°,连接AE. (1)、求证:△CEA≌△CDB;(2)、求证:AE2+AD2=DE2 .22. 如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=6,动点P从点B出发,以每秒2个单位长的速度,沿射线BC运动,设运动时间为t秒,请解答以下问题:
(1)、求证:△CEA≌△CDB;(2)、求证:AE2+AD2=DE2 .22. 如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=6,动点P从点B出发,以每秒2个单位长的速度,沿射线BC运动,设运动时间为t秒,请解答以下问题: (1)、BC边的长为;(2)、当△ABP为直角三角形时,求t的值,写出求解过程;(3)、当△ABP为等腰三角形时,直接写出t的值.23. 如图,四边形ACDE是证明勾股定理时用到的图形,a,b,c是Rt△ABC和Rt△BED边长,易知AE= c,这时我们把关于x的形如ax2+ cx+b=0的一元二次方程称为“勾系一元二次方程”.
(1)、BC边的长为;(2)、当△ABP为直角三角形时,求t的值,写出求解过程;(3)、当△ABP为等腰三角形时,直接写出t的值.23. 如图,四边形ACDE是证明勾股定理时用到的图形,a,b,c是Rt△ABC和Rt△BED边长,易知AE= c,这时我们把关于x的形如ax2+ cx+b=0的一元二次方程称为“勾系一元二次方程”.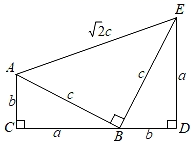 (1)、写出一个“勾系一元二次方程” .(2)、求证:关于x的“勾系一元二次方程”ax2+ cx+b=0必有实数根.(3)、若x=﹣1是“勾系一元二次方程”ax2+ cx+b=0的一个根,且△ABC的面积是25,求四边形ACDE的周长.
(1)、写出一个“勾系一元二次方程” .(2)、求证:关于x的“勾系一元二次方程”ax2+ cx+b=0必有实数根.(3)、若x=﹣1是“勾系一元二次方程”ax2+ cx+b=0的一个根,且△ABC的面积是25,求四边形ACDE的周长.