安徽省滁州市定远县吴圩片2021-2022学年八年级下学期5月调研考试数学试题

试卷更新日期：2023-01-13 类型：月考试卷

进入出卷网下载

一、单选题

1. 实数 $a ， b$ 在数轴上对应点的位置如图所示，且 $| a | > | b |$ ，则化简 $\sqrt{a^{2}} + | a + b |$ 的结果为（）

A、 $2 a + b$ B、 $- 2 a - b$ C、 $b$ D、 $2 a - b$

查看试题解析
2. 已知 $y = \sqrt{x - 2} + \sqrt{2 - x} - \sqrt{3}$ ，则 $(x + y)^{2020} (x - y)^{2021}$ 的值为（）

A、 $2 - \sqrt{3}$ B、 $2 + \sqrt{3}$ C、-1 D、1

查看试题解析
3. 关于 $x$ 的一元二次方程 $(m - 3) x^{2} + m^{2} x = 9 x + 5$ 化为一般形式后不含一次项，则 $m$ 的值为（）

A、0 B、 $\pm 3$ C、3 D、-3

查看试题解析
4. 如果关于 $x$ 的方程 $(m - 1) x^{2} + x + 1 = 0$ 有实数根，那么 $m$ 的取值范围是（）

A、 $m < \frac{5}{4}$ B、 $m < \frac{5}{4}$ 且 $m \neq 1$ C、 $m \leq \frac{5}{4}$ D、 $m \leq \frac{5}{4}$ 且 $m \neq 1$

查看试题解析
5. 如图，在长为80米，宽为60米的矩形场地上修建两条宽度相等且互相垂直的道路，剩余部分进行绿化，要使绿化面积为 $4661 m^{2}$ ，则道路的宽应为多少米？设道路的宽为x米，则可列方程为（）

A、 $80 \times 60 - 80 x - 60 x = 4661$ B、 $(80 - x) (60 - x) + x^{2} = 4661$ C、 $(80 - x) (60 - x) = 4661$ D、 $80 x + 60 x = 80 \times 60 - 4661$

查看试题解析
6. 已知Rt $△$ ABC中，∠ACB＝90°，AC＝BC，AB＝4 $\sqrt{2}$ ，D为BC的中点，E是线段AB上一点，连接CE、DE，则CE+DE的最小值是（）

A、2 $\sqrt{3}$ B、2 $\sqrt{5}$ C、4 $\sqrt{2}$ D、2+2 $\sqrt{2}$

查看试题解析
7. 如图，长方形纸片ABCD中，AB=3cm，AD=9cm，将此长方形纸片折叠，使点D与点B重合，点C落在点H的位置，折痕为EF ，则△ABE的面积为（）

A、6cm² B、8cm² C、10cm² D、12cm²

查看试题解析
8. 已知实数a，b，c，是 $△ A B C$ 三边的长，且满足等式 $a + b = \sqrt{2} c$ ， $a b = \frac{1}{2} c^{2}$ ，则关于 $△ A B C$ 的形状最准确的描述是（）

A、等边三角形 B、等腰三角形 C、直角三角形 D、等腰直角三角形

查看试题解析
9. 如图，在四边形ABCD中，∠A=140°，∠D=90°，OB平分∠ABC，OC平分∠BCD，则∠BOC=(　　)

A、105° B、115° C、125° D、135°

查看试题解析
10. 如图，在 $▱ A B C D$ 中，点E，F分别在边AB，AD上，将△AEF沿EF折叠，点A恰好落在BC边上的点G处，若 $∠ A = 4 5^{∘}$ ， $A B = 6 \sqrt{2}$ ， $5 B E = A E$ ，则AF长度为（）

A、 $\frac{15}{2}$ B、7 C、6 D、20

查看试题解析

二、填空题

11. 函数 $y = \frac{\sqrt{2 x - 4}}{x - 1}$ 的自变量 $x$ 的取值范围是．

查看试题解析
12. 若关于x的一元二次方程 $2 x^{2} - 3 x + m = 0$ 的一个实数根是 $x = 3$ ，则m的值为．

查看试题解析
13. 在《九章算术》中有一个问题（如图)：今有竹高一丈，末折抵地，去本三尺，问折者高几何?它的意思是：一根竹子原高一丈（ $10$ 尺)，中部一处折断，竹梢触地面处离竹根 $3$ 尺，试问折断处离地面尺．

查看试题解析
14. 将等边三角形、正方形、正五边形按如图所示的位置摆放．若 $∠ 3 = 11 °$ ， $∠ 2 = 51 °$ ，则 $∠ 1$ 的度数为．

查看试题解析

三、解答题

15.

(1)、已知： $y = \frac{\sqrt{x^{2} - 4} + \sqrt{4 - x^{2}}}{x - 2} + 3$ ，求yx．

(2)、已知 $x = \sqrt{3} + \sqrt{2} ， y = \sqrt{3} - \sqrt{2}$ ，求x²y+xy²的值．

查看试题解析
16. 如图1，图2分别是某种型号拉杆箱的实物图与示意图，根据商品介绍，获得了如下信息：滑竿DE、箱长BC拉杆AB的长度都相等，即DE=BC=AB=50，点B、F在线段AC上，点C在DE上，支杆DF=30cm．

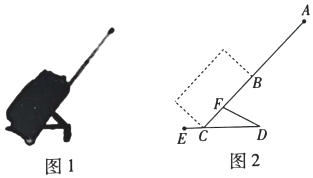(1)、若EC=36cm时，B，D相距48cm，试判定BD与DE的位置关系，并说明理由；

(2)、当∠DCF＝45°，CF＝ $\frac{1}{5}$ AC时，求CD的长．

查看试题解析
17. 如图，在正方形网格中，每个小正方形的边长为1．

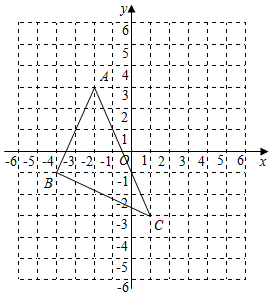(1)、在图中画出以AC为对角线的平行四边形ABCD；

(2)、写出D的坐标和平行四边形ABCD的面积．

查看试题解析
18. 我们已经学习了利用配方法解一元二次方程，其实配方法还有其他重要应用．
例：已知 $x$ 可取任何实数，试求二次三项式 $x^{2} + 6 x - 1$ 最小值．
解： $x^{2} + 6 x - 1 = x^{2} + 2 \times 3 \cdot x + 3^{2} - 3^{2} - 1$
$= (x + 3)^{2} - 10$
$∵$ 无论 $x$ 取何实数，总有 $(x + 3)^{2} ⩾ 0$ ．
$∵ (x + 3)^{2} - 10 ⩾ - 10$ ，即 $x^{2} + 6 x - 1$ 的最小值是-10．
即无论 $x$ 取何实数， $x^{2} + 6 x - 1$ 的值总是不小于-10的实数．

(1)、问题：
已知 $y = x^{2} - 4 x + 7$ ，求证 $y$ 是正数．

(2)、知识迁移：
如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 6 c m$ ， $B C = 4 c m$ ，点 $P$ 在边 $A C$ 上，从点 $A$ 向点 $C$ 以 $2 c m / s$ 的速度移动，点 $Q$ 在 $C B$ 边上以 $\sqrt{3} c m / s$ 的速度从点 $C$ 向点 $B$ 移动．若点 $P$ ， $Q$ 同时出发，且当一点移动到终点时，另一点也随之停止，设 $Δ P C Q$ 的面积为 $S c m^{2}$ ，运动时间为 $t$ 秒，求 $S$ 的最大值．

查看试题解析
19. 已知关于x的一元二次方程 $(a - 3) x^{2} - 6 x + 8 = 0$ .

(1)、若方程的一个根为 $x = - 1$ ，求a的值；

(2)、若方程有实数根，求满足条件的正整数a的值.

查看试题解析
20. 如图，田村有一口呈四边形的池塘，在它的四个角A、B、C、D处均种有一棵大核桃树．田村准备开挖池塘建养鱼池，想使池塘面积扩大一倍，又想保持核桃树不动，并要求扩建后的池塘成平行四边形的形状，请问田村能否实现这一设想？若能，请你设计并画出图形；若不能，请说明理由（画图要保留痕迹，不写画法）．

查看试题解析
21. 我们根据图形的移、拼、补可以简单直观地推理验证数学规律和公式，这种方法称之为“无字证明”，它比严谨的数学证明更为优雅与有条理．下面是用三块全等的直角三角形移、拼、补所形成的“无字证明”图形．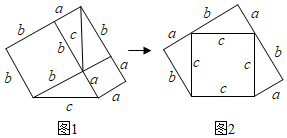

(1)、此图可以用来证明你学过的什么定理？请写出定理的内容；

(2)、已知直角三角形直角边长分别为a、b，斜边长为c，图1、图2的面积相等，请你根据此图证明（1）中的定理．

查看试题解析
22. 【问题提出】在2020年抗击新冠肺炎的斗争中，某中学响应政府“停课不停学”的号召进行线上学习，七年级一班的全体同学在自主完成学习任务的同时，全班每两个同学都通过一次视频电话，彼此关怀，互相勉励，共同提高，若每两名同学之间仅通过一次视频电话，如何求全班50名同学共通过多少次电话呢？
【模型构建】用点M₁、M₂、M₃、…、M₅₀分别表示第1、2、3、…、50名同学，把该班级人数n与视频通话次数S之间的关系用如图模型表示：

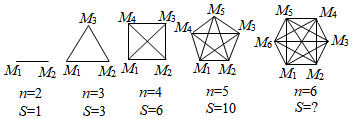(1)、【问题解决】
填写如图中第5个图中S的值为．

(2)、通过探索发现，通电话次数S与该班级人数n之间的关系式为，则当n＝50时，对应的S＝．

(3)、若该班全体女生相互之间共通话190次，求该班共有多少名女生？

(4)、【问题拓展】
若该班数学兴趣小组的同学，每两位同学之间互发一条微信问候，小明统计全组共发送微信110条，则该班数学兴趣小组的人数是人．

查看试题解析
23. 如图，在四边形ABCD中，AB∥CD，∠ADC＝90°，E为BC的中点，连接DE并延长，与AB的延长线交于点F，连接BD、FC．

(1)、求证：四边形BFCD是平行四边形；

(2)、连接AE，若CD＝2，AD＝3，AB＝4，求AE的长．

查看试题解析