2023年中考数学精选真题实战测试26 二次函数 B
试卷更新日期:2023-01-13 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 关于二次函数 ,下列说法正确的是( )A、函数图象的开口向下 B、函数图象的顶点坐标是 C、该函数有最大值,是大值是5 D、当 时,y随x的增大而增大2. 如图,已如抛物线 开口向上,与 轴的一个交点为 ,对称轴为直线 .下列结论错误的是( )
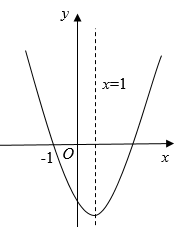 A、 B、 C、 D、3. 已知二次函数 , 当时,y的最小值为 , 则a的值为( )A、或4 B、或 C、或4 D、或44. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( )
A、 B、 C、 D、3. 已知二次函数 , 当时,y的最小值为 , 则a的值为( )A、或4 B、或 C、或4 D、或44. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( ) A、
A、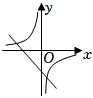 B、
B、 C、
C、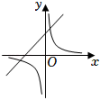 D、
D、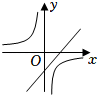 5. 在平面直角坐标系中,将二次函数的图象向左平移1个单位长度,再向下平移2个单位长度,所得函数的解析式为( )A、 B、 C、 D、6. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,其对称轴为直线x=﹣ , 且与x轴的一个交点坐标为(﹣2,0).下列结论:①abc>0;②a=b;③2a+c=0;④关于x的一元二次方程ax2+bx+c﹣1=0有两个相等的实数根.其中正确结论的序号是( )
5. 在平面直角坐标系中,将二次函数的图象向左平移1个单位长度,再向下平移2个单位长度,所得函数的解析式为( )A、 B、 C、 D、6. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,其对称轴为直线x=﹣ , 且与x轴的一个交点坐标为(﹣2,0).下列结论:①abc>0;②a=b;③2a+c=0;④关于x的一元二次方程ax2+bx+c﹣1=0有两个相等的实数根.其中正确结论的序号是( )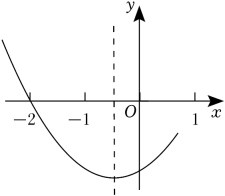 A、①③ B、②④ C、③④ D、②③7. 已知抛物线y=ax2 +bx +c的对称轴为x=1,与x轴正半轴的交点为A(3,0),其部分图象如图所示,有下列结论:①abc >0;②2c﹣3b <0;③5a +b+2c=0;④若B( , y1)、C( , y2)、D( , y3)是抛物线上的三点,则y1<y2<y3.其中正确结论的个数有( )
A、①③ B、②④ C、③④ D、②③7. 已知抛物线y=ax2 +bx +c的对称轴为x=1,与x轴正半轴的交点为A(3,0),其部分图象如图所示,有下列结论:①abc >0;②2c﹣3b <0;③5a +b+2c=0;④若B( , y1)、C( , y2)、D( , y3)是抛物线上的三点,则y1<y2<y3.其中正确结论的个数有( )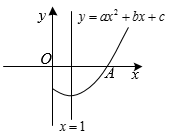 A、1 B、2 C、3 D、48. 如图,在中,对角线相交于点O, , 若过点O且与边分别相交于点E,F,设 , 则y关于x的函数图象大致为( )
A、1 B、2 C、3 D、48. 如图,在中,对角线相交于点O, , 若过点O且与边分别相交于点E,F,设 , 则y关于x的函数图象大致为( )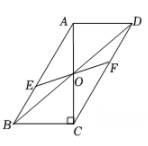 A、
A、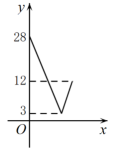 B、
B、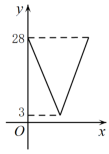 C、
C、 D、
D、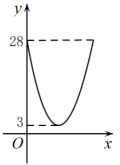 9. 已知抛物线 , 当时,;当时,.下列判断:
9. 已知抛物线 , 当时,;当时,.下列判断:①;②若 , 则;③已知点 , 在抛物线上,当时,;④若方程的两实数根为 , , 则.
其中正确的有( )个.
A、1 B、2 C、3 D、410. 已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为 , 且经过点(-1,0).下列结论:①3a+b=0;②若点 , (3,y2)是抛物线上的两点,则y1<y2;③10b-3c=0;④若y≤c,则0≤x≤3.其中正确的有( )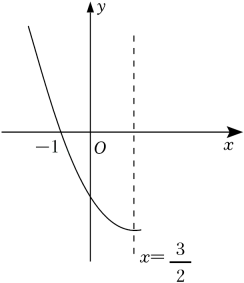 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每空3分,共18分)
-
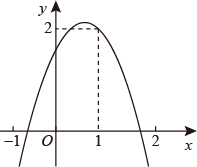
11. 若二次函数的图象上有且只有三个点到x轴的距离等于m,则m的值为 .12. 如图,二次函数 的函数图象经过点(1,2),且与 轴交点的横坐标分别为 、 ,其中 -1< <0,1< <2,下列结论:① ;② ;③ ;④当 时, ;⑤ ,其中正确的有 .(填写正确的序号)
 13. 如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度 (单位:m)与飞行时间 (单位:s)之间具有函数关系: ,则当小球飞行高度达到最高时,飞行时间 s.
13. 如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度 (单位:m)与飞行时间 (单位:s)之间具有函数关系: ,则当小球飞行高度达到最高时,飞行时间 s. 14. 若点在二次函数的图象上,且点到轴的距离小于2,则的取值范围是 .15. 已知二次函数 , 当时,函数值y的最小值为1,则a的值为 .16. 小明在学习“二次函数”内容后,进行了反思总结.如图,二次函数y=ax2+bx+c(a≠0)图像的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图像他得出下列结论:①ab>0且c>0;②a+b+c=0;③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为﹣3和1;④若点(﹣4,y1),(﹣2,y2),(3,y3)均在二次函数图象上,则y1<y2<y3;⑤3a+c<0,其中正确的结论有 . (填序号,多选、少选、错选都不得分)
14. 若点在二次函数的图象上,且点到轴的距离小于2,则的取值范围是 .15. 已知二次函数 , 当时,函数值y的最小值为1,则a的值为 .16. 小明在学习“二次函数”内容后,进行了反思总结.如图,二次函数y=ax2+bx+c(a≠0)图像的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图像他得出下列结论:①ab>0且c>0;②a+b+c=0;③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为﹣3和1;④若点(﹣4,y1),(﹣2,y2),(3,y3)均在二次函数图象上,则y1<y2<y3;⑤3a+c<0,其中正确的结论有 . (填序号,多选、少选、错选都不得分)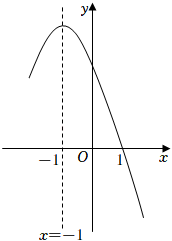
三、解答题(共7题,共72分)
-
17. 根据以下素材,探索完成任务.
如何设计拱桥景观灯的悬挂方案?
素材1
图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽 20m ,拱顶离水面 5m .据调查,该河段水位在此基础上再涨 1.8m 达到最高.
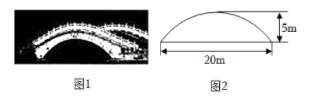
素材2
为迎佳节,拟在图1桥洞前面的桥拱上悬挂 40cm 长的灯笼,如图3.为了安全,灯笼底部距离水面不小于 1m ;为了实效,相邻两盏灯笼悬挂点的水平间距均为 1.6m ;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.
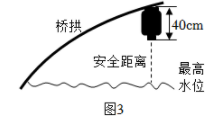
问题解决
任务1
确定桥拱形状
在图2中建立合适的直角坐标系,求抛物线的函数表达式.
任务2
探究悬挂范围
在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.
任务3
拟定设计方案
给出一种符合所有悬挂条件的灯笼数量,并根据你所建立的坐标系,求出最左边一盏灯笼悬挂点的横坐标.
18. 丹东是我国的边境城市,拥有丰富的旅游资源.某景区研发一款纪念品,每件成本为30元,投放景区内进行销售,规定销售单价不低于成本且不高于54元,销售一段时间调研发现,每天的销售数量y(件)与销售单价x(元/件)满足一次函数关系,部分数据如下表所示:销售单价x(元/件)
…
35
40
45
…
每天销售数量y(件)
…
90
80
70
…
(1)、直接写出y与x的函数关系式;(2)、若每天销售所得利润为1200元,那么销售单价应定为多少元?(3)、当销售单价为多少元时,每天获利最大?最大利润是多少元?19. 如图,平行四边形中,边上的高 , 点E为边上的动点(不与B、C重合,过点E作直线的垂线,垂足为F,连接 . (1)、求证:;(2)、当点E为的中点时,求的长;(3)、设的面积为y,求y与x之间的函数关系式,并求当x为何值时,y有最大值,最大值是多少?20. 抛物线与x轴交于 , 两点,与y轴交于点C,直线y=kx-6经过点B.点P在抛物线上,设点P的横坐标为m.
(1)、求证:;(2)、当点E为的中点时,求的长;(3)、设的面积为y,求y与x之间的函数关系式,并求当x为何值时,y有最大值,最大值是多少?20. 抛物线与x轴交于 , 两点,与y轴交于点C,直线y=kx-6经过点B.点P在抛物线上,设点P的横坐标为m.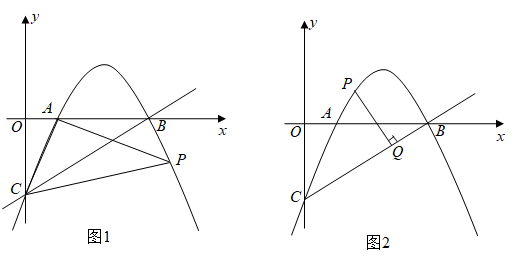 (1)、求抛物线的表达式和t,k的值;(2)、如图1,连接AC,AP,PC,若△APC是以CP为斜边的直角三角形,求点P的坐标;(3)、如图2,若点P在直线BC上方的抛物线上,过点P作PQ⊥BC,垂足为Q,求的最大值.21. 如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过A( , 0),B(3,)两点,与y轴交于点C.
(1)、求抛物线的表达式和t,k的值;(2)、如图1,连接AC,AP,PC,若△APC是以CP为斜边的直角三角形,求点P的坐标;(3)、如图2,若点P在直线BC上方的抛物线上,过点P作PQ⊥BC,垂足为Q,求的最大值.21. 如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过A( , 0),B(3,)两点,与y轴交于点C.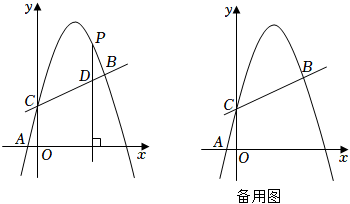 (1)、求抛物线的解析式;(2)、点P在抛物线上,过P作PD⊥x轴,交直线BC于点D,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;(3)、抛物线上是否存在点Q,使∠QCB=45°?若存在,请直接写出点Q的坐标;若不存在,请说明理由.22. 定义:函数图象上到两坐标轴的距离都不大于的点叫做这个函数图象的“n阶方点”.例如,点是函数图像的“阶方点”;点是函数图像的“2阶方点”.(1)、在①;②;③三点中,是反比例函数图像的“1阶方点”的有(填序号);(2)、若y关于x的一次函数图像的“2阶方点”有且只有一个,求a的值;(3)、若y关于x的二次函数图像的“n阶方点”一定存在,请直接写出n的取值范围.23. 如图,在平面直角坐标系中,经过点的直线AB与y轴交于点 . 经过原点O的抛物线交直线AB于点A,C,抛物线的顶点为D.
(1)、求抛物线的解析式;(2)、点P在抛物线上,过P作PD⊥x轴,交直线BC于点D,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;(3)、抛物线上是否存在点Q,使∠QCB=45°?若存在,请直接写出点Q的坐标;若不存在,请说明理由.22. 定义:函数图象上到两坐标轴的距离都不大于的点叫做这个函数图象的“n阶方点”.例如,点是函数图像的“阶方点”;点是函数图像的“2阶方点”.(1)、在①;②;③三点中,是反比例函数图像的“1阶方点”的有(填序号);(2)、若y关于x的一次函数图像的“2阶方点”有且只有一个,求a的值;(3)、若y关于x的二次函数图像的“n阶方点”一定存在,请直接写出n的取值范围.23. 如图,在平面直角坐标系中,经过点的直线AB与y轴交于点 . 经过原点O的抛物线交直线AB于点A,C,抛物线的顶点为D.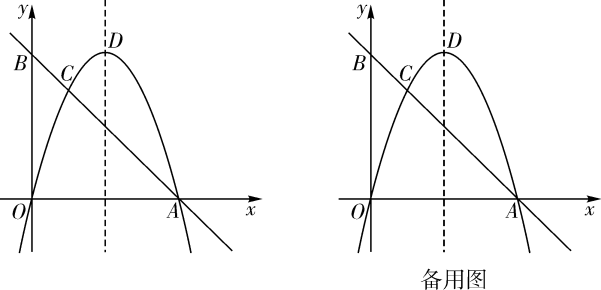 (1)、求抛物线的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当轴且时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当轴且时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.