（华师大版）2022-2023学年八年级数学下册17.5 实践与探索 同步测试
试卷更新日期：2023-01-13 类型：同步测试
一、单选题
-
1. 网语期印，李明同学在老家学习生活，为缓解线上学习疲劳，在某个周末和爸爸进行登山锻炼，登山过程中，两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示(甲为爸爸，乙为李明)，李明提速后，李明的登山速度是原来速度的2倍，并先到达山顶.根据图象所提供的信息，下列说法情误的是（ ）
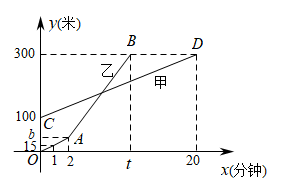A、甲登山的速度是每分钟米 B、乙在A地时距地面的高度b为米 C、乙登山分钟时追上甲 D、登山时间为5分钟、8分钟、分钟时，甲、乙两人距地面的高度差为米2. “漏壶”是古代一种计时器，在它内部盛一定量的水，不考虑水量变化对压力的影响，水从壶底小孔均匀漏出，壶内壁有刻度.人们根据壶中水面的位置计算时间.在漏壶漏完水之前，漏壶内水的深度与对应的漏水时间满足的函数关系式（ ）
A、正比例函数关系 B、一次函数关系 C、反比例函数关系 D、二次函数关系3. 弹簧的长度与所挂物体的质量的关系为一次函数，如图所示，由此图可知不挂物体时弹簧的长度为（ ）
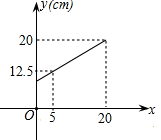A、7cm B、8cm C、9cm D、10cm4. 漏刻是我国古代的一种计时工具，据史书记载，西周时期就已经出现了漏刻，这是中国古代人民对函数思想的创造性应用，小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型，研究中发现水位h(cm)是时间t(min)的一次函数，如下表是小明记录的部分数据，其中有一个h的值记录不符合题意，请排除后利用正确的数据确定当时间t为8时，对应的高度h为（ ）t（min）
……
0
1
2
3
……
h（cm）
……
0.7
1.2
1.5
1.9
……
A、3.3 B、3.65 C、3.9 D、4.75. 已知蓄电池的电压为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位：）是反比例函数关系，它的图象如图所示．下列说法正确的是（ ）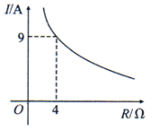
A、函数解析式为 B、蓄电池的电压是18V C、当时， D、当时，6. 如图，在弹性限度内，弹簧的长度y（cm）与所挂物体的质量x（kg）之间是一次函数关系，则弹簧不挂物体时的长度为（ ）
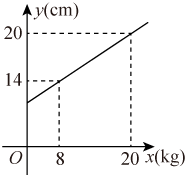A、8cm B、10cm C、11cm D、12cm7. 小明同学在一次学科综合实践活动中发现，某品牌鞋子的长度y cm与鞋子的码数x之间满足一次函数关系，下表给出y与x的一些对应值：码数x
26
30
34
42
长度y cm
18
20
22
26
根据小明的数据，可以得出该品牌38码鞋子的长度为（ ）
A、24cm B、25cm C、26cm D、38cm8. 在物理实验课上，小鹏利用滑轮组及相关器材进行实验，他把得到的拉力和所悬挂物体的重力的几组数据用电脑绘制成如下图象（不计绳重和摩擦），请你根据图象判断以下结论正确的序号有（ ）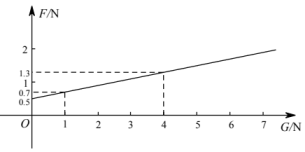
①物体的拉力随着重力的增加而增大；②当物体的重力N时，拉力N；③拉力F与重力G成正比例函数关系；④当滑轮组不悬挂物体时，所用拉力为0.5N．
A、①② B、②④ C、①④ D、③④9. 甲、乙两车沿同一条路从地出发匀速行驶至相距的地，甲出发1小时后乙再出发，如图表示甲、乙两车离开地的距离与乙出发的时间之间的关系，下列结论错误的是（ ）
A、甲车的速度是 B、乙车的速度是 C、的值为60，的值为4 D、甲车出发后被乙车追上10. 如图所示的图象（折线ABCDE）描述了一辆汽车在某一直线上的行驶过程中，汽车离出发地的距离s（千米）与行驶时间t（时）之间的关系，根据图象信息，下列说法正确的是（ ）
A、汽车共行驶了140千米 B、汽车在行驶途中停留了1小时 C、汽车在整个行驶过程中的平均速度为30千米/时 D、汽车出发后6小时至9小时之间行驶的速度在逐渐减小二、填空题
-
11. 在弹簧限度内，弹簧挂上物体后弹簧的长度与所挂物体的质量之间的关系如表：
所挂物体的质量/千克
1
2
3
4
5
6
7
8
弹簧的长度/cm
12.5
13
13.5
14
14.5
15
15.5
16
则不挂物体时，弹簧的长度是cm．
12. 如图，折线表示从甲地向乙地打电话所需的电话费（元）关于通话时间（分钟）的函数图象，则通话7分钟需要支付电话费元．
13. 一辆汽车前灯电路上的电压U（V）保持不变，选用灯泡的电阻为R（Ω），通过的电流强度为I（A），由欧姆定律可知，I ． 当电阻为40Ω时，测得通过的电流强度为0.3A．为保证电流强度不低于0.2A且不超过0.6A，则选用灯泡电阻R的取值范围是 ．14. 弹簧的长度（cm）与所挂物体的质量（kg）之间的关系如图所示，那么弹簧不挂物体时的长度是cm．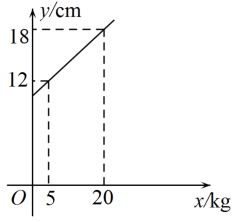
15. 某苹果种植合作社通过网络销售苹果，如图所示的线段AB反映了苹果的日销售量y（千克）与销售单价x（元/千克）间的函数关系，已知1千克苹果的成本是5元，如果某天该合作社的苹果销售单价为8元/千克，那么这天销售苹果的盈利是 元．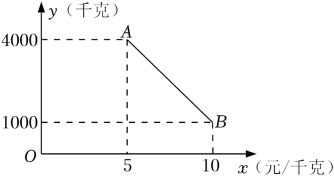
三、解答题
-
16. 一辆轿车在高速公路上匀速行使，油箱存油量Q（升）与行使的路程S（km）成一次函数关系.若行使100km时，油箱存油43.5升，当行使300km时，油箱存油30.5升，请求出这个一次函数关系式，并写出自变量S的取值范围.17. 为了预防新冠肺炎，某药店欲购进甲、乙两种防护口罩进行销售，有关信息如表：
进价（元/袋）
售价（元/袋）
甲种防护口罩
20
25
乙种防护口罩
30
37
该药店准备购进甲、乙两种防护口罩共40袋，且甲种防护口罩不少于30袋，问应该怎样进货，才能使总获利最大，最大利润为多少元？
18. 2022年5月8日是“母亲节”，小明买了一束百合和康乃馨组合的鲜花送给妈妈，以表祝福.在买花过程中，爱思考的小明发现一个数学问题：3支康乃馨的价格比2支百合的价格多2元，买2支百合和1支康乃馨共花费14元.如果买一束百合和康乃馨组合的鲜花共11支，且百合不少于2支，那么怎样组合，能使费用支出最少？请你帮助小明解决这个数学问题.四、综合题
-
19. 在某一电路中，保持电压U不变，电流I（单位：A）与电阻R（单位：）成反比例关系，当电阻时，电流 ．(1)、求I与R之间的函数关系式；(2)、当电流时，求电阻R的值．20. 某蔬菜生产基地的气温较低时，用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后，大棚内的温度y（℃）与时间x（h）之间的函数关系，其中线段AB、BC表示恒温系统开启阶段，双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题：
(1)、求这天的温度y与时间x（0≤x≤24）的函数关系式；(2)、恒温系统设定的恒定温度为；(3)、若大棚内的温度低于10℃时，蔬菜会受到伤害.问这天内，为避免蔬菜受到伤害，恒温系统最多可以关闭多少小时？21. 为了节能减排，我市某校准备购买某种品牌的节能灯，已知3只A型节能灯和5只B型节能灯共需50元，1只A型节能灯和3只B型节能灯共需26元．(1)、求1只A型节能灯和1只B型节能灯的售价各是多少元．(2)、学校准备购买这两种型号的节能灯共200只，要求购买A型号的节能灯a只，记购买两种型号的节能灯的总费用为W元．①求W与a的函数关系式；
②当时，求购买两种型号的节能灯的总费用是多少？
22. 为满足顾客的购物需求，某水果店计划购进甲、乙两种水果进行销售．经了解，购进2千克甲水果和3千克乙水果共需23元，购进3千克甲水果和1千克乙水果共需17元，已知甲，乙两种水果的售价分别为6元/千克和10元/千克．(1)、求甲、乙两种水果的进价分别是多少？(2)、若水果店购进这两种水果共200千克，其中甲种水果的重量不低于乙种水果重量的1.5倍，则水果店应如何进货才能获得最大利润，最大利润是多少？23. 如图1是甲、乙两个圆柱形水槽的轴截面示意图，乙槽中有一圆柱形实心铁块立放其中（圆柱形铁块的下底面完全落在乙槽底面上）.现将甲槽中的水匀速注入乙槽，甲、乙两个水槽中水的深度与注水时间之间的关系如图2.根据图象提供的信息，解答下列问题：
(1)、图2中折线表示槽中水的深度与注水时间之间的关系，线段表示槽中水的深度与注水时间之间的关系（以上两空填“甲”或“乙”），槽中铁块的高度是；(2)、注水多长时间时，甲、乙两个水槽中水的深度相同；(3)、若乙槽底面积为（壁厚不计），求乙槽中铁块的体积.