（华师大版）2022-2023学年八年级数学下册17.4 反比例函数同步测试

试卷更新日期：2023-01-13 类型：同步测试

进入出卷网下载

一、单选题

1. 下列关系中，两个量之间为反比例关系的是（）

A、正方形的面积S与边长a的关系 B、正方形的周长L与边长a的关系 C、矩形的长为a，宽为20，其面积S与a的关系 D、矩形面积为40，长为a，宽为b，a与b的关系

查看试题解析
2. 下列函数中，表示y是x的反比例函数的是（）

A、 $y = \sqrt{3} x$ B、 $y = \frac{a}{x}$ C、 $y = \frac{1}{x^{2}}$ D、 $y = \frac{1}{3 x}$

查看试题解析
3. 若反比例函数 $y = \frac{2}{x}$ 中， $x$ 与 $y$ 的值相等，则这个相等的值为（）

A、2 B、 $\pm \sqrt{2}$ C、 $\sqrt{2}$ D、 $- \sqrt{2}$

查看试题解析
4. 已知反比例函数 $y = \frac{k}{x} (k \neq 0)$ ，当自变量 $x$ 的值从3增加到6时，函数值减少了1，则函数的表达式为（）

A、 $y = \frac{6}{x}$ B、 $y = \frac{3}{x}$ C、 $y = \frac{2}{x}$ D、 $y = \frac{1}{2 x}$

查看试题解析
5. 在反比例函数 $y = \frac{m - 1}{x}$ 中， $m$ 的取值范围是（ )

A、 $m \neq 1$ B、 $m > 1$ C、 $m > 0$ D、 $m \neq 0$

查看试题解析
6. 有下列函数：① $y = \frac{π}{x}$ ；② $y = - \sqrt{3} x$ ；③ $y = - \frac{5}{2 x}$ ；④ $y = \frac{5}{x^{2}}$ ；⑤ $y = \frac{2}{x - 1}$ ；⑥ $y = \frac{1}{x} - 3$ .其中 $y$ 是 $x$ 的反比例函数的有（ )

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 已知点A（3，4）在反比例函数 $y = \frac{k}{x} (k$ 为常数， $k \neq 0)$ 的图象上，则该反比例函数的解析式是（）

A、 $y = \frac{3}{x}$ B、y= $\frac{4}{x}$ C、y= $\frac{12}{x}$ D、y= $\frac{7}{x}$

查看试题解析
8. 已知 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ， $C (x_{3} ， y_{3})$ 是反比例函数 $y = - \frac{4}{x}$ 图象上的三个点，且 $x_{1} < 0 < x_{2} < x_{3}$ ，那么 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{3} > y_{2} > y_{1}$ B、 $y_{1} > y_{2} > y_{3}$ C、 $y_{1} > y_{3} > y_{2}$ D、 $y_{2} > y_{3} > y_{1}$

查看试题解析
9. $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ 是反比例函数 $y = \frac{6}{x}$ 的图象上的两点，若 $2 < x_{1} < x_{2}$ ，则下列结论正确的是（）

A、 $3 < y_{1} < y_{2}$ B、 $3 < y_{2} < y_{1}$ C、 $y_{1} < y_{2} < 3$ D、 $y_{2} < y_{1} < 3$

查看试题解析
10. 要确定方程 $x^{2} + x - 5 = 0$ 的解，只需知道一次函数 $y = x + 1$ 和反比例函数 $y = \frac{k}{x}$ 的图象交点的横坐标．由上面的信息可知， $k$ 的值为（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

11. 若 $y = \frac{m - 1}{x^{| m |}}$ 是反比例函数，则m的值为；

查看试题解析
12. 油箱注满 $k$ 升油后，轿车可行驶的总路程 $S$ (单位：千米)与平均耗油量 $a$ (单位：升/千米)之间是反比例函数关系 $S = \frac{k}{a}$ ( $k$ 是常数， $k \neq 0)$ .已知某轿车油箱注满油后，以平均耗油量为每千米0.1升的速度行驶，可行驶700千米.则该轿车可行驶的总路程 $S$ 与平均耗油量 $a$ 之间的函数关系式为.

查看试题解析
13. 在平面直角坐标系中，若点 $(- 2 ， y_{1})$ 、 $(1 ， y_{2})$ 、 $(- 1 ， y_{3})$ 都在函数 $y = \frac{k}{x} (k < 0)$ 的图象上，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系是（用“＞”号连接）．

查看试题解析
14. 已知一次函数 $y_{1} = a x + b$ 与反比例函数 $y_{2} = \frac{k}{x}$ 的图象如图所示．在第一象限内，当 $y_{1} > y_{2}$ 时，则 $x$ 的取值范围是．

查看试题解析
15. 已知反比例函数 $y = \frac{1 - m}{x}$ 的图象的一支位于第一象限，则常数m的取值范围是．

查看试题解析

三、解答题

16. 某市为促进经济发展，增强对外贸易的竞争力，把距离港口360千米的普通公路升级成了同等长度的高速公路，结果汽车行驶的平均速度比原来提高了50%，行驶时间缩短了2小时，求汽车原来的平均速度.

查看试题解析
17. 已知反比例函数y= $(2 m - 1) x^{m^{2} - 2}$ ，当x＞0时，y随着x的增大而减小．

（1）求m的值；

（2）当1＜x＜4时，求y的取值范围．

查看试题解析
18. 为了做好校园疫情防控工作，学校后勤每天对全校办公室和教室进行药物喷洒消毒，完成1间教室的药物喷洒要5min ，药物喷洒时教室内空气中的药物浓度 $y$ （单位： ${mg/m}^{3}$ ）与时间 $x$ （单位：min）的函数关系式为 $y = 2 x$ ，其图象为图中线段 $O A$ ，药物喷洒完成后 $y$ 与 $x$ 成反比例函数关系，两个函数图象的交点为 $A (m ， n)$ ，当教室空气中的药物浓度不高于 ${1mg/m}^{3}$ 时，对人体健康无危害，如果后勤人员依次对一班至十一班教室（共11间）进行药物喷洒消毒当最后一间教室药物喷洒完成后，一班能否能让人进入教室？请通过计算说明.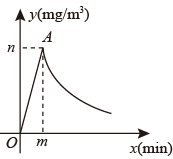

查看试题解析

四、综合题

19. 已知水池的容量一定，当每小时的灌水量 $q = 3 (m^{8})$ 时，溸满水池所需的时间为 $t = 12 (h)$ .

(1)、写出每小时灌水量q与灌满水池所需时间t之间的函数关系式及t的取值范围；

(2)、当灌满水池需要8h时，求每小时的灌水量.

查看试题解析
20. 面积一定的梯形，其上底长是下底长的 $\frac{1}{3}$ ，设上底长为xcm，高为ycm，且当x=5时，y=6.

(1)、求y与x的函数关系式；

(2)、求当y=4时下底的长.

查看试题解析
21. 某运输公司承担某项工程的运送土石方任务.已知需要运送的土石方总量为 $4 \times 10^{4}$ 立方米，设运输公司每天运送的土石方为 $V$ (立方米/天)，完成任务所需要的时间为 $t$ （天).

(1)、 $V$ 与 $t$ 之间有怎样的函数关系？

(2)、运输公司共派出20辆卡车，每辆卡车每天可运送土石方100立方米，工程进行了8天后，如果需要提前4天才能完成任务，那么该运输公司至少需要增派多少辆同样的卡车才能按时完成任务？

查看试题解析
22. 华润苏果超市计划购进甲、乙两种商品，已知甲的进价比乙多20元/件，用2000元购进甲种商品的件数与用1600元购进乙种商品的件数相同.

(1)、求甲、乙两种商品的进价各是多少元？

(2)、小丽用960元只购买乙种商品，她购买乙种商品 $y$ 件，该商品的销售单价为 $x$ 元，列出 $y$ 与 $x$ 函数关系式？若超市销售乙种商品，至少要获得20%的利润，那么小丽最多可以购买多少件乙种商品？

查看试题解析
23. 心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化．开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB，BC分别为线段，CD为双曲线的一部分)．

(1)、开始上课后第5分钟时与第30分钟时相比较，何时学生的注意力更集中？

(2)、一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？

查看试题解析

（华师大版）2022-2023学年八年级数学下册17.4 反比例函数 同步测试

一、单选题

二、填空题

三、解答题

四、综合题

（华师大版）2022-2023学年八年级数学下册17.4 反比例函数同步测试