（华师大版）2022-2023学年八年级数学下册17.3 一次函数同步测试

试卷更新日期：2023-01-13 类型：同步测试

进入出卷网下载

一、单选题

1. 下列函数中，y是x的一次函数的是（）

A、y＝ $\frac{x}{2}$ B、y＝-x²+3 C、y＝ $\frac{1}{x}$ D、y＝2（1-x）+2x

查看试题解析
2. 某商场自行车存放处每周的存车量为6000辆次，其中变速车存车费是每辆每次1元，普通车存车费为每辆每次0.5元，若这周普通车存车量为 $x$ 辆次，存车的总收入为 $y$ 元，则 $y$ 与 $x$ 之间的关系式是（）

A、 $y = 0.5 x + 6000$ B、 $y = - 0.5 x + 6000$ C、 $y = 0.5 x + 3000$ D、 $y = - 0.5 x + 3000$

查看试题解析
3. 已知函数y＝（m﹣3） $x^{m^{2} - 8}$ +4是关于x的一次函数，则m的值是（　　）

A、m＝±3 B、m≠3 C、m＝3 D、m＝﹣3

查看试题解析
4. 如图，佳佳设计了一种挖宝游戏，屏幕上正方形 $A B C D$ 是宝藏区（含正方形边界），其中 $A (1 ， 1)$ ， $B (2 ， 1)$ ，沿直线 $y = x + b$ 行走，则游戏者能够挖到宝藏的b的取值范围为（）

A、 $- 1 \leq b \leq 2$ B、 $- 2 \leq b \leq 1$ C、 $- 1 \leq b \leq 1$ D、 $b \leq 1$

查看试题解析
5. 在平面直角坐标系中，将直线 $l_{1}$ ： $y = 2 x - 2$ 平移后得到直线 $l_{2}$ ： $y = 2 x + 4$ ，则下列平移方法正确的是（）

A、将 $l_{1}$ 向上平移4个单位长度 B、将 $l_{1}$ 向下平移6个单位长度 C、将 $l_{1}$ 向左平移3个单位长度 D、将 $l_{1}$ 向右平移3个单位长度

查看试题解析
6. 下列正比例函数中，y随x的增大而增大的是（）

A、 $y = 2 x$ B、 $y = - 2 x$ C、 $y = - \frac{1}{2} x$ D、 $y = - 8 x$

查看试题解析
7. 已知正比例函数 $y = (1 - m) x$ 的图像上一点 $(a ， b)$ ，且 $a b < 0$ ，则m的值可能是（）

A、-0.5 B、0 C、1 D、1.5

查看试题解析
8. 网语期印，李明同学在老家学习生活，为缓解线上学习疲劳，在某个周末和爸爸进行登山锻炼，登山过程中，两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示(甲为爸爸，乙为李明)，李明提速后，李明的登山速度是原来速度的2倍，并先到达山顶.根据图象所提供的信息，下列说法情误的是（）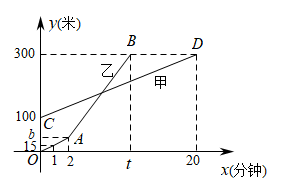

A、甲登山的速度是每分钟 $10$ 米 B、乙在A地时距地面的高度b为 $30$ 米 C、乙登山 $5.5$ 分钟时追上甲 D、登山时间为5分钟、8分钟、 $17$ 分钟时，甲、乙两人距地面的高度差为 $30$ 米

查看试题解析
9. “漏壶”是古代一种计时器，在它内部盛一定量的水，不考虑水量变化对压力的影响，水从壶底小孔均匀漏出，壶内壁有刻度.人们根据壶中水面的位置计算时间.在漏壶漏完水之前，漏壶内水的深度与对应的漏水时间满足的函数关系式（）

A、正比例函数关系 B、一次函数关系 C、反比例函数关系 D、二次函数关系

查看试题解析
10. 弹簧的长度与所挂物体的质量的关系为一次函数，如图所示，由此图可知不挂物体时弹簧的长度为（）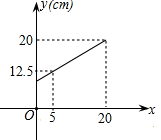

A、7cm B、8cm C、9cm D、10cm

查看试题解析

二、填空题

11. 今年9月30日，太忻大道忻州段正式通车，标志着太忻大道全线通车．太忻大道南起太原市阳兴大道，北至忻州市忻府区，双向六车道．小王驾车从太忻大道南起点处出发，向北终点处匀速行驶，他离终点的路程y（千米）与行驶时间x（时）之间的部分对应值如表所示，则y与x之间的函数表达式为．
x
0
0.1
0.2
0.3
0.4
y
41
35
29
23
17

查看试题解析
12. 已知一次函数y＝ax+b，且2a+b＝1，则该一次函数图象必经过点.

查看试题解析
13. 若点 $(- 2 ， y_{1})$ ， $(5 ， y_{2})$ 在一次函数 $y = - 4 x - 3$ 的图象上，则 $y_{1}$ ， $y_{2}$ 的大小关系是.（用“<”连接）

查看试题解析
14. 已知一次函数 $y = - 5 x + 3$ ，若函数 $y$ 满足 $- 7 < y < 23$ ，则自变量 $x$ 的取值范围是．

查看试题解析
15. 已知三点 $(1 ， - 1)$ ， $(2 ， - 3)$ ， $(a ， 7)$ 在同一条直线上，则a的值为

查看试题解析

三、解答题

16. 如图，已知正比例函数的表达式为y＝﹣ $\frac{1}{2}$ x，过正比例函数在第四象限图象上的一点A作x轴的垂线，交x轴于点H，AH＝2，求线段OA的长．

查看试题解析
17. 一次函数图象经过（3,1），（2,0）两点．

(1)、求这个一次函数的解析式；

(2)、求当x=6时，y的值．

查看试题解析
18. 在平面直角坐标系中，一条直线经过 $A (- 1 ， 5)$ ， $B (a ， - 3)$ ， $C (3 ， 13)$ 三点．求这条直线的解析式并求出a的值．

查看试题解析

四、综合题

19. 将长为38cm，宽为5cm的长万形白纸拔如图所示的方法黏合在一起，黏合部分的白纸宽为2cm．

(1)、求5张白纸黏合的长度：

(2)、设x张白纸黏合后的总长为ycm，写出y与x的函数关系式

查看试题解析
20. 已知： $y$ 与 $x + 2$ 成正比例，且当 $x = 1$ 时， $y = - 6$ ．

(1)、求 $y$ 与 $x$ 之间的函数解析式；

(2)、若点 $M (m ， 4)$ 在这个函数的图象上，求 $m$ 的值．

查看试题解析
21. 夏季来临，某商场准备购进甲、乙两种空调，其中甲种空调比乙种空调进价每台少500元，用40000元购进甲种空调数量与用50000元购进乙种空调数量相同．该商场计划一次性从空调生产厂家购进甲、乙两种空调共100台，其中乙种空调的数量不超过甲种空调的2倍．若甲种空调每台售价2400元，乙种空调每台售价3000元．请解答下列问题：

(1)、求甲、乙两种空调每台的进价分别是多少元?

(2)、设购进甲种空调x台，100台空调的销售总利润为y元，该商店购进甲、乙两种空调各多少台才能使销售总利润最大，最大利润是多少？

(3)、在（2）的条件下，商场拿出一部分利润购买A、B两种轮椅捐赠给敬老院，已知A种轮椅一台300元，B种轮椅一台400元，最后商场仅剩利润38600元，请直接写出商场有几种购买方案．

查看试题解析
22. 已知 $y + 1$ 与 $x - 2$ 成正比例，且当 $x = 1$ 时， $y = - 3$ .

(1)、求 $y$ 与 $x$ 的函数关系式；

(2)、判断点 $(- 1 ， - 5)$ 是否在该函数的图象上.

查看试题解析
23. 我区应国家号召，认真贯彻落实党的二十大精神，全面推进乡村振兴，把富民政策一项一项落实好，特将农户种植的农产品包装成A、B两种大礼包.某超市预购进两种大礼包共400个，两种大礼包的进价和预售价如表.设购进A种大礼包x个，且所购进的两种大礼包能全部卖完时获得的总利润为W元.

大礼包类型

进价/（元/个）

售价/（元/个）

A

47

65

B

37

50

(1)、求W关于x的函数表达式（不要求写x的取值范围）；

(2)、如果购进两种大礼包的总费用不超过18000元，那么商场如何进货才能获得最大利润？最大利润是多少？

查看试题解析

大礼包类型	进价/（元/个）	售价/（元/个）
A	47	65
B	37	50

x	0	0.1	0.2	0.3	0.4
y	41	35	29	23	17

（华师大版）2022-2023学年八年级数学下册17.3 一次函数 同步测试

一、单选题

二、填空题

三、解答题

四、综合题

（华师大版）2022-2023学年八年级数学下册17.3 一次函数同步测试