(华师大版)2022-2023学年八年级数学下册17.1变量与函数 同步测试
试卷更新日期:2023-01-13 类型:同步测试
一、单选题
-
1. 一本笔记本5元,买x本共付y元,则变量是( )A、5 B、5和x C、x D、x和y2. 一个圆形花坛,面积S与半径的函数关系式中关于常量和变量的表述正确的是( )A、常量是2,变量是、、 B、常量是2、 , 变量是、 C、常量是2,变量是、 D、常量是 , 变量是、3. 下列曲线中,不能表示y是x的函数的是( )A、
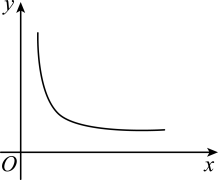 B、
B、 C、
C、 D、
D、 4. 对于函数y=x+1,自变量x取5时,对应的函数值为( )A、3 B、36 C、16 D、65. 下列所描述的四个变化过程中,变量之间的关系不能看成函数关系的是( )A、三角形的一个外角度数度和与它相邻的内角度数度的关系 B、树的高度为60厘米,每个月长高3厘米,月后树的高度为厘米,与的关系 C、正方形的面积(平方厘米)和它的边长(厘米)的关系 D、一个正数的平方根是 , 随着这个数的变化而变化,与之间的关系6. 一辆汽车以60km/h的速度行驶,行驶的路程与行驶的时间t(h)之间的关系式为s=60t,其中变量是( )A、速度与路程 B、速度与时间 C、路程与时间 D、三者均为变量7. 函数 中,自变量 的取值范围是( )A、 B、 C、 D、8. 一本笔记本5元,买本共付元,则5和分别是( )A、常量,常量 B、变量,变量 C、常量,变量 D、变量,常量9. 函数的自变量取值范围是( )A、 B、 C、 D、且10. 如图所示图象表示的两个变量间的关系中,y不是x的函数的是( )A、
4. 对于函数y=x+1,自变量x取5时,对应的函数值为( )A、3 B、36 C、16 D、65. 下列所描述的四个变化过程中,变量之间的关系不能看成函数关系的是( )A、三角形的一个外角度数度和与它相邻的内角度数度的关系 B、树的高度为60厘米,每个月长高3厘米,月后树的高度为厘米,与的关系 C、正方形的面积(平方厘米)和它的边长(厘米)的关系 D、一个正数的平方根是 , 随着这个数的变化而变化,与之间的关系6. 一辆汽车以60km/h的速度行驶,行驶的路程与行驶的时间t(h)之间的关系式为s=60t,其中变量是( )A、速度与路程 B、速度与时间 C、路程与时间 D、三者均为变量7. 函数 中,自变量 的取值范围是( )A、 B、 C、 D、8. 一本笔记本5元,买本共付元,则5和分别是( )A、常量,常量 B、变量,变量 C、常量,变量 D、变量,常量9. 函数的自变量取值范围是( )A、 B、 C、 D、且10. 如图所示图象表示的两个变量间的关系中,y不是x的函数的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 当时,函数的值是 .12. 函数中,自变量x的取值范围是 .13. 如图,在平面直角坐标系xOy中,四边形OBCD是正方形,点B(1,0),请写出一个图象与该正方形有公共点的函数表达式: .
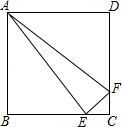
 14. 已知等边 的边长为 是边 上一点,DE∥BC交边 于点 ,以 为一边在 形内构造矩形DEFG. 且 .设 , 则 关于 的函数关系式是 (无需写出定义域).
14. 已知等边 的边长为 是边 上一点,DE∥BC交边 于点 ,以 为一边在 形内构造矩形DEFG. 且 .设 , 则 关于 的函数关系式是 (无需写出定义域). 15. 函数中,自变量的取值范围是 .
15. 函数中,自变量的取值范围是 .三、解答题
-
16. 如图,正方形ABCD的边长为4cm,E,F分别是BC,CD边上一动点,点E,F同时从点C出发,以每秒2cm的速度分别向点B,D运动,当点E与点B重合时,运动停止,设运动时间为x(s),运动过程中△AEF的面积为y(cm2),求y关于x的函数表达式,并写出自变量x的取值范围.
 17. 物体从高处自由下落的高度h(m)与物体下落的时间t(s)之间的函数关系式是:h= gt2(g表示重力加速度,g取9.8m/s2).某人发现头顶上空490m处有一炸弹自由下落,其地面杀伤半径为50m,此人发现后,立即以6m/s的速度逃离,那么此人有无危险?18. 为了增强居民的节水意识,某城区水价执行“阶梯式”计费,每月应缴水费y(元)与用水量x(t)之间的函数关系如图所示.若某用户去年5月缴水费18.05元,求该用户当月用水量.
17. 物体从高处自由下落的高度h(m)与物体下落的时间t(s)之间的函数关系式是:h= gt2(g表示重力加速度,g取9.8m/s2).某人发现头顶上空490m处有一炸弹自由下落,其地面杀伤半径为50m,此人发现后,立即以6m/s的速度逃离,那么此人有无危险?18. 为了增强居民的节水意识,某城区水价执行“阶梯式”计费,每月应缴水费y(元)与用水量x(t)之间的函数关系如图所示.若某用户去年5月缴水费18.05元,求该用户当月用水量.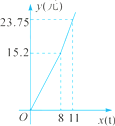
四、综合题
-
19. 已知函数表达式 .(1)、在下表的两个空格中分别填入适当的数;
x
5
500
5000
50000
…
1.2
1.02
1.002
1.0002
…
(2)、观察上表可知,当x的值越来越大时,对应的y值越来越接近于一个常数,这个常数是什么?20. 已知与x成正比例,当时, .(1)、求y与x的函数表达式;(2)、当时,求y的值.21. 某同学根据学习函数的经验,对函数的图像与性质进行了探究.下面是他的探究过程,请补充完整∶ (1)、填表
(1)、填表x
…
-5
-4
-3
-2
-1
0
1
2
3
4
…
y
…
-1
-1
-1
0
1
3
…
(2)、根据(1)中的结果,请在所给坐标系中画出函数的图像.(3)、结合函数图象,请写出该函数的一条性质.22. 司机小王开车从地出发去地送信,其行驶路与行驶时间之间的关系如图所示,当汽车行驶若干小时到达地时,汽车发生了故障,需停车检修,修理了几小时后,为了按时赶到地,汽车加快了速度,结果正好按时赶到,根据题意结合图回答下列问题: (1)、上述问题中反映的是哪两个变量之间的关系?指出自变量和因变量.(2)、汽车从地到地用了几小时?平均每小时行驶多少千米?(3)、汽车停车检修了多长时间?车修好后每小时走多少千米?23. 在一条笔直的滑道上有黑、白两个小球同向运动,黑球在处开始减速,此时白球在黑球前面处.
(1)、上述问题中反映的是哪两个变量之间的关系?指出自变量和因变量.(2)、汽车从地到地用了几小时?平均每小时行驶多少千米?(3)、汽车停车检修了多长时间?车修好后每小时走多少千米?23. 在一条笔直的滑道上有黑、白两个小球同向运动,黑球在处开始减速,此时白球在黑球前面处.
小聪测量黑球减速后的运动速度(单位:)、运动距离(单位:)随运动时间(单位:)变化的数据,整理得下表.
运动时间
0
1
2
3
4
运动速度
10
9.5
9
8.5
8
运动距离
0
9.75
19
27.75
36
小聪探究发现,黑球的运动速度与运动时间之间成一次函数关系,运动距离与运动时间之间成二次函数关系.
(1)、直接写出关于的函数解析式和关于的函数解析式(不要求写出自变量的取值范围)(2)、当黑球减速后运动距离为时,求它此时的运动速度;(3)、若白球一直以的速度匀速运动,问黑球在运动过程中会不会碰到白球?请说明理由.