2023年中考数学精选真题实战测试24 反比例函数 B
试卷更新日期:2023-01-13 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 点 , , , 在反比例函数 图象上,则 , , , 中最小的是( )A、 B、 C、 D、2. 如图,一次函数与反比例函数的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为 , 则不等式的解集是( )
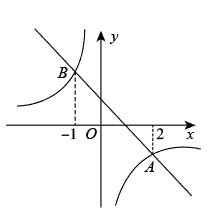 A、或 B、或 C、或 D、3. 如图是反比例函数y=的图象,点A(x,y)是反比例函数图象上任意一点,过点A作AB⊥x轴于点B,连接OA,则△AOB的面积是( )
A、或 B、或 C、或 D、3. 如图是反比例函数y=的图象,点A(x,y)是反比例函数图象上任意一点,过点A作AB⊥x轴于点B,连接OA,则△AOB的面积是( )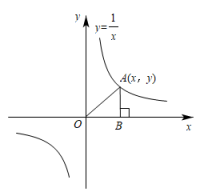 A、1 B、 C、2 D、4. 一次函数 与反比例函数 在同一坐标系中的大致图象是( )A、
A、1 B、 C、2 D、4. 一次函数 与反比例函数 在同一坐标系中的大致图象是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,正方形ABCD的边长为5,点A的坐标为(4,0),点B在y轴上,若反比例函数y=(k≠0)的图像过点C,则k的值为( )
5. 如图,正方形ABCD的边长为5,点A的坐标为(4,0),点B在y轴上,若反比例函数y=(k≠0)的图像过点C,则k的值为( )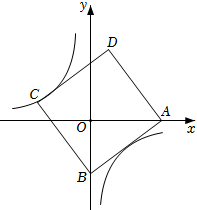 A、4 B、﹣4 C、﹣3 D、36. 如图,直线AB交x轴于点C,交反比例函数y=(a>1)的图象于A、B两点,过点B作BD⊥y轴,垂足为点D,若S△BCD=5,则a的值为( )
A、4 B、﹣4 C、﹣3 D、36. 如图,直线AB交x轴于点C,交反比例函数y=(a>1)的图象于A、B两点,过点B作BD⊥y轴,垂足为点D,若S△BCD=5,则a的值为( ) A、8 B、9 C、10 D、117. 如图,在四边形 中, , , , 平分 .设 , ,则 关于 的函数关系用图象大致可以表示为( )
A、8 B、9 C、10 D、117. 如图,在四边形 中, , , , 平分 .设 , ,则 关于 的函数关系用图象大致可以表示为( )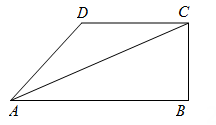 A、
A、 B、
B、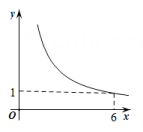 C、
C、 D、
D、 8. 一次函数y=mx+n的图象与反比例函数y= 的图象交于点A、B,其中点A、B的坐标为A(- ,-2m)、B(m,1),则△OAB的面积( )A、3 B、 C、 D、9. 如图,点A在反比例函数的图象上,以为一边作等腰直角三角形 , 其中∠=90°, , 则线段长的最小值是( )
8. 一次函数y=mx+n的图象与反比例函数y= 的图象交于点A、B,其中点A、B的坐标为A(- ,-2m)、B(m,1),则△OAB的面积( )A、3 B、 C、 D、9. 如图,点A在反比例函数的图象上,以为一边作等腰直角三角形 , 其中∠=90°, , 则线段长的最小值是( )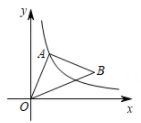 A、1 B、 C、 D、410. 如图,点是内一点,与轴平行,与轴平行, , , , 若反比例函数的图象经过 , 两点,则k的值是( )
A、1 B、 C、 D、410. 如图,点是内一点,与轴平行,与轴平行, , , , 若反比例函数的图象经过 , 两点,则k的值是( )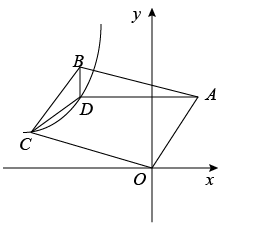 A、 B、-6 C、 D、-12
A、 B、-6 C、 D、-12二、填空题(每空3分,共18分)
-
11. 平面直角坐标系中,已知点是函数图象上的三点。若 , 则k的值为 .12. 如图,在直角坐标系中,△ABC的顶点C与原点O重合,点A在反比例函数y= (k>0,x>0)的图象上,点B的坐标为(4,3),AB与y轴平行,若AB=BC,则k= .
 13. 如图,点A、B在反比例函数的图象上,轴,垂足为D,.若四边形间面积为6, , 则k的值为.
13. 如图,点A、B在反比例函数的图象上,轴,垂足为D,.若四边形间面积为6, , 则k的值为.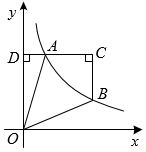 14. 如图,平行四边形OABC的顶点O是坐标原点,A在x轴的正半轴上,B,C在第一象限,反比例函数的图象经过点C,的图象经过点B.若 , 则k= .
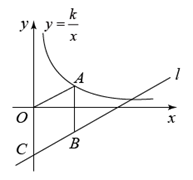
14. 如图,平行四边形OABC的顶点O是坐标原点,A在x轴的正半轴上,B,C在第一象限,反比例函数的图象经过点C,的图象经过点B.若 , 则k= . 15. 如图,点A在双曲线 上,点B在直线 上,A与B关于x轴对称,直线l与y轴交于点C,当四边形 是菱形时,有以下结论:
15. 如图,点A在双曲线 上,点B在直线 上,A与B关于x轴对称,直线l与y轴交于点C,当四边形 是菱形时,有以下结论:① ②当 时, ③ ④
则所有正确结论的序号是 .
 16. 如图,在平面直角坐标系中, 斜边上的高为1, ,将 绕原点顺时针旋转 得到 ,点A的对应点C恰好在函数 的图象上,若在 的图象上另有一点M使得 ,则点M的坐标为.
16. 如图,在平面直角坐标系中, 斜边上的高为1, ,将 绕原点顺时针旋转 得到 ,点A的对应点C恰好在函数 的图象上,若在 的图象上另有一点M使得 ,则点M的坐标为.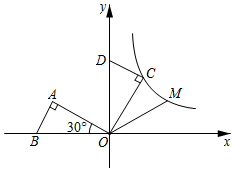
三、解答题(共8题,共72分)
-
17. 如图,在平面直角坐标系 中,一次函数 的图像与反比例函数 的图像交于 、 两点.点 ,点 的纵坐标为-2.
 (1)、求反比例函数与一次函数的表达式;(2)、求 的面积.18. 如图,已知直线l:y=x+4与反比例函数y=(x<0)的图象交于点A(−1,n),直线l′经过点A,且与l关于直线x=−1对称.
(1)、求反比例函数与一次函数的表达式;(2)、求 的面积.18. 如图,已知直线l:y=x+4与反比例函数y=(x<0)的图象交于点A(−1,n),直线l′经过点A,且与l关于直线x=−1对称. (1)、求反比例函数的解析式;(2)、求图中阴影部分的面积.19. 如图,点A在第一象限内,AB⊥x轴于点B,反比例函数 的图象分别交AO,AB于点C,D.已知点C的坐标为(2,2),BD=1.
(1)、求反比例函数的解析式;(2)、求图中阴影部分的面积.19. 如图,点A在第一象限内,AB⊥x轴于点B,反比例函数 的图象分别交AO,AB于点C,D.已知点C的坐标为(2,2),BD=1. (1)、求k的值及点D的坐标.(2)、已知点P在该反比例函数图象上,且在△ABO的内部(包括边界),直接写出点P的横坐标x的取值范围.20. 如图, , , 点A,B分别在函数()和()的图象上,且点A的坐标为.
(1)、求k的值及点D的坐标.(2)、已知点P在该反比例函数图象上,且在△ABO的内部(包括边界),直接写出点P的横坐标x的取值范围.20. 如图, , , 点A,B分别在函数()和()的图象上,且点A的坐标为.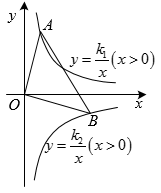 (1)、求 , 的值:(2)、若点C,D分在函数()和()的图象上,且不与点A,B重合,是否存在点C,D,使得 , 若存在,请直接出点C,D的坐标:若不存在,请说明理由.21. 已知直线与反比例函数的图象在第一象限交于点.
(1)、求 , 的值:(2)、若点C,D分在函数()和()的图象上,且不与点A,B重合,是否存在点C,D,使得 , 若存在,请直接出点C,D的坐标:若不存在,请说明理由.21. 已知直线与反比例函数的图象在第一象限交于点.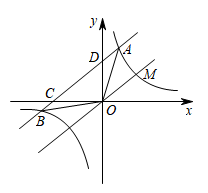 (1)、求反比例函数的解析式;(2)、如图,将直线向上平移个单位后与的图象交于点和点 , 求的值;(3)、在(2)的条件下,设直线与轴、轴分别交于点 , , 求证:.22. 如图,反比例函数与正比例函数的图象交于点和点 , 点是点关于轴的对称点,连接 , .
(1)、求反比例函数的解析式;(2)、如图,将直线向上平移个单位后与的图象交于点和点 , 求的值;(3)、在(2)的条件下,设直线与轴、轴分别交于点 , , 求证:.22. 如图,反比例函数与正比例函数的图象交于点和点 , 点是点关于轴的对称点,连接 , .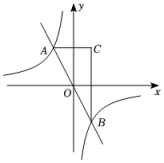 (1)、求该反比例函数的解析式;(2)、求的面积;(3)、请结合函数图象,直接写出不等式的解集.23. 如图,已知一次函数的图象与函数的图象交于 , 两点,与轴交于点将直线沿轴向上平移个单位长度得到直线 , 与轴交于点.
(1)、求该反比例函数的解析式;(2)、求的面积;(3)、请结合函数图象,直接写出不等式的解集.23. 如图,已知一次函数的图象与函数的图象交于 , 两点,与轴交于点将直线沿轴向上平移个单位长度得到直线 , 与轴交于点. (1)、求与的解析式;(2)、观察图象,直接写出时的取值范围;(3)、连接 , , 若的面积为6,则的值为.24. 小华同学学习函数知识后,对函数 通过列表、描点、连线,画出了如图1所示的图象.
(1)、求与的解析式;(2)、观察图象,直接写出时的取值范围;(3)、连接 , , 若的面积为6,则的值为.24. 小华同学学习函数知识后,对函数 通过列表、描点、连线,画出了如图1所示的图象.x
…
-4
-3
-2
-1
0
1
2
3
4
…
y
…
1
2
4
1
0
-4
-2
-1
…

请根据图象解答:
(1)、【观察发现】
①写出函数的两条性质:;;
②若函数图象上的两点 , 满足 ,则 一定成立吗?.(填“一定”或“不一定”)
(2)、【延伸探究】如图2,将过 , 两点的直线向下平移n个单位长度后,得到直线l与函数 的图象交于点P,连接PA,PB.①求当n=3时,直线l的解析式和△PAB的面积;
②直接用含n的代数式表示△PAB的面积.