2022-2023学年初数北师大版八年级下册1.3 线段的垂直平分线同步训练必刷题
试卷更新日期:2023-01-13 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=3cm,则线段PB的长为( )
 A、6cm B、5cm C、4cm D、3cm2. 如图,在中, , 垂直平分 , 垂足为 , 交于 , 若 , 则的周长为( )
A、6cm B、5cm C、4cm D、3cm2. 如图,在中, , 垂直平分 , 垂足为 , 交于 , 若 , 则的周长为( ) A、 B、 C、 D、3. 如图,的周长为 , 垂直平分 , 交于点E,交于点D,连接 , , 则的周长为( )
A、 B、 C、 D、3. 如图,的周长为 , 垂直平分 , 交于点E,交于点D,连接 , , 则的周长为( ) A、 B、 C、 D、4. 如图,在△ABC中,∠C=85°,∠B=30°,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,交BC于点D,连接AD,则∠CAD的度数为( )
A、 B、 C、 D、4. 如图,在△ABC中,∠C=85°,∠B=30°,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,交BC于点D,连接AD,则∠CAD的度数为( ) A、50° B、45° C、35° D、30°5. 如图,中,的垂直平分线分别交于点 , 则的度数为( )
A、50° B、45° C、35° D、30°5. 如图,中,的垂直平分线分别交于点 , 则的度数为( ) A、 B、 C、 D、6. 如图, , , B点在的垂直平分线上,若 , 则为( )
A、 B、 C、 D、6. 如图, , , B点在的垂直平分线上,若 , 则为( ) A、4 B、6 C、8 D、107. 如图,A,B,C三个村庄围成了一个三角形,想在的内部建一个超市,且超市到三个村庄的距离相等,则此超市应建在( )
A、4 B、6 C、8 D、107. 如图,A,B,C三个村庄围成了一个三角形,想在的内部建一个超市,且超市到三个村庄的距离相等,则此超市应建在( ) A、三条高的交点处 B、三条角平分线的交点处 C、三条边垂直平分线的交点处 D、三条中线的交点处8. 如图,在中, , 分别以点,点为圆心以大于为半径画弧,两弧交于 , , 连接交于点 , 连接 , 以为圆心,长为半径作弧,交于点,则:( )
A、三条高的交点处 B、三条角平分线的交点处 C、三条边垂直平分线的交点处 D、三条中线的交点处8. 如图,在中, , 分别以点,点为圆心以大于为半径画弧,两弧交于 , , 连接交于点 , 连接 , 以为圆心,长为半径作弧,交于点,则:( ) A、1: B、1:2 C、1: D、1:9. 如图,DE 是△ABC中AC边的垂直平分线,若BC=8厘米,AB=10厘米,则△EBC的周长为( )
A、1: B、1:2 C、1: D、1:9. 如图,DE 是△ABC中AC边的垂直平分线,若BC=8厘米,AB=10厘米,则△EBC的周长为( ) A、16 B、18 C、26 D、2810. 如图,在矩形中, , 对角线与相交于点O, , 垂足为E, , 则的长为( ).
A、16 B、18 C、26 D、2810. 如图,在矩形中, , 对角线与相交于点O, , 垂足为E, , 则的长为( ). A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共30分)
-
11. 如图,是的边的垂直平分线,垂足为点E,交于点D,连接 , , , , 则的长为.
 12. 如图,在锐角△ABC中,∠A=75°,DE和DF分别垂直平分边AB、AC,则∠DBC的度数为 °.
12. 如图,在锐角△ABC中,∠A=75°,DE和DF分别垂直平分边AB、AC,则∠DBC的度数为 °.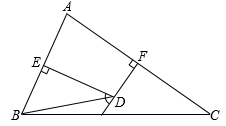 13. 如图,DE是△ABC中AC边的垂直平分线,若BC=8cm,AB=10cm,则△EBC的周长为cm.
13. 如图,DE是△ABC中AC边的垂直平分线,若BC=8cm,AB=10cm,则△EBC的周长为cm. 14. 如图,在△ABC中,AB的中垂线DE交AC于点D,已知BC=10,△BDC的周长为25,则AC=.
14. 如图,在△ABC中,AB的中垂线DE交AC于点D,已知BC=10,△BDC的周长为25,则AC=. 15. 如图,△ABC中,BC的垂直平分线DP与∠BAC的角平分线相交于点D,垂足为点P,若∠BAC=84°,则∠BDC=.
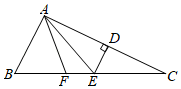
15. 如图,△ABC中,BC的垂直平分线DP与∠BAC的角平分线相交于点D,垂足为点P,若∠BAC=84°,则∠BDC=. 16. 如图,在△ABC中,∠ACB=90°,∠B=30°,AB=10,点D为斜边AB的中点,点P是直角边BC上一动点,连结AP,DP,则AP+DP的最小值为。
16. 如图,在△ABC中,∠ACB=90°,∠B=30°,AB=10,点D为斜边AB的中点,点P是直角边BC上一动点,连结AP,DP,则AP+DP的最小值为。 17. 在中,的垂直平分线分别交 , 于点、 , 的垂直平分线分别交 , 于点、 , 若 , , 且的周长为16,求.
17. 在中,的垂直平分线分别交 , 于点、 , 的垂直平分线分别交 , 于点、 , 若 , , 且的周长为16,求. 18. 如图,已知三内角的角平分线交于点D,三边的垂直平分线交于点E,若 , 则度.
18. 如图,已知三内角的角平分线交于点D,三边的垂直平分线交于点E,若 , 则度. 19. 如图,在直角三角形ABC中, , , 点D是的中点,点P是斜边上的一个动点,是线段的垂直平分线,Q是上的一个动点,则的最小值为.
19. 如图,在直角三角形ABC中, , , 点D是的中点,点P是斜边上的一个动点,是线段的垂直平分线,Q是上的一个动点,则的最小值为.
三、解答题(共6题,共60分)
-
20. 如图,在△ABC中,AF平分∠BAC交BC于点F,AC的垂直平分线交BC于点E,交AC于点D,∠B=60°,∠C=26°,求∠FAE的度数.
 21. 已知在中,∠CAB的平分线AD与BC的垂直平分线DE交于点D, DM丄AB与M, DN丄AC交AC的延长线于N,你认为BM与CN之间有什么关系?试证明你的发现.
21. 已知在中,∠CAB的平分线AD与BC的垂直平分线DE交于点D, DM丄AB与M, DN丄AC交AC的延长线于N,你认为BM与CN之间有什么关系?试证明你的发现.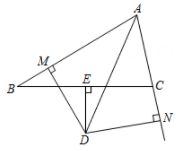 22. 如图,在中, , .
22. 如图,在中, , . (1)、作线段的垂直平分线交于D(保留作图痕迹).(2)、求证:.
(1)、作线段的垂直平分线交于D(保留作图痕迹).(2)、求证:.


