2022-2023学年初数北师大版八年级下册1.1 等腰三角形同步训练必刷题
试卷更新日期：2023-01-13 类型：同步测试
一、单选题（每题3分，共30分）
-
1. 等腰三角形的一个角是50°，则它的底角是（ ）A、50° B、50°或65° C、80°或50° D、65°2. 如图，在△ABC 中，AB＝AC，∠A＝36°，BD、CE 分别是∠ABC、∠ACB 的平分线，则图中的等腰三角形有（ ）
A、5 个 B、6 个 C、7 个 D、8 个3. 若一个等腰三角形的周长是10，其中一边长为2，则这个等腰三角形底边的长度为（ ）A、2或6 B、6 C、2或8 D、24. 如图，在中， ， ， 以点C为圆心，长为半径作弧交于点D，分别以点A和点D为圆心，大于长为半径作弧，两弧相交于点E，作直线 ， 交于点F，则的度数是（ ）
A、 B、 C、 D、5. 如图，是一钢架， ， 为使钢架更加牢固，需在其内部添加一些钢管 ， ， ， …，添加的钢管长度都与的长度相等，则最多能添加的钢管根数为（ ）
A、4 B、5 C、6 D、无数6. 下列命题中，假命题的是（ ）A、等腰三角形的两个底角相等 B、直角三角形的两个锐角互余 C、有两个内角是 60°的三角形是等边三角 D、等腰三角形的两个底角的平分线互相垂直7. 如图，已知△ABC是等边三角形，点B、C、D、E在同一直线上，且CG=CD，DF=DE，则∠E的度数为（ ）
A、25° B、20° C、15° D、7.5°8. 如图，△ABC和△DCE都是边长为4的等边三角形，点B、C、E在同一条直线上，连接BD，则BD的长为（ ）
A、 B、 C、 D、9. 下列命题宜用反证法证明的是（ ）A、等腰三角形两腰上的高相等 B、有一个外角是120°的等腰三角形是等边三角形 C、在同一平面内，若两条直线都与第三条直线平行，则这两条直线互相平行 D、全等三角形的面积相等10. 如图，将矩形纸片ABCD沿EF翻折，使点A与点C重合，E，F分别在AB，CD上，下列结论；① ；② 为等腰三角形；③延长GF，则GF必经过点A；④若 为等边三角形，则 .其中正确结论的个数是（ ）
A、1 B、2 C、3 D、4二、填空题
-
11. 等腰三角形一边长是10cm，一边长是6cm，则它的周长是12. 等腰三角形一腰上的中线将它的周长分为15和18两部分，则它的腰长为 ．13. 如图，平面直角坐标系中，点A（0，3）和B（4，0），点M（8，m）为坐标平面内一动点，且ΔABM为等腰三角形，则点M的坐标为 ．
14. 若实数a、b满足等式 ，且a，b恰好是等腰三角形ABC的边长，则这个等腰三角形的周长是.15. 如图，已知△ABC是等边三角形， ∠BCD ＝90°，BC＝CD，则∠BAD＝
16. 如图，已知P、Q是 ABC的边BC上的两点，且BP=QC=PQ=AP=AQ，则∠BAC=
17. 如图，等边△ABC中，AD是中线，AD=AE，则∠EDC= ．
18. 如图，等腰△ABC的底边BC＝20，面积为160，点F是BC边上的一个动点，EG是腰AC的垂直平分线，若点D在EG上运动，则CD+DF的最小值为 ．
三、解答题（共6题，共60分）
-
19. 如图，在中，交于点交于点.求证：是等边三角形.
20. 如图，△ABC是等边三角形，BD平分∠ABC，延长BC到E，使得CE=CD．求证：BD=DE．
21. 如图，△ABC是等边三角形，△BDC是顶角∠BDC=120°的等腰三角形，M是AB延长线上一点，N是CA延长线上一点，且∠MDN=60°．试探BM，MN，CN之间的数量关系，并给出证明．
22. 如图，在中，点、分别是边、上的点， ， 连接、 ， 与交于点 ， 且 ．
(1)、求证：是等腰三角形；(2)、若 ， ， 求的度数．23. 已知，如图，在△ABC中，AB=AC，∠BAC=120°，AP⊥BC，垂足为D，且AP=AB．
(1)、求证：△ABP是等边三角形；(2)、若E是边AB上一点，∠EPF=60°，PF交AC于点F，试判断BE与AF的数量关系，并说明理由．24.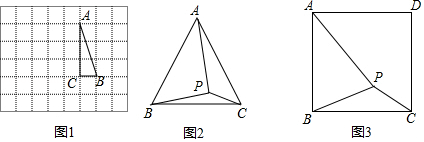
(1)、（操作发现）如图1，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．请接要求画图：将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B′，点C的对应点为C′，连接BB′，则∠AB′B＝ ．
(2)、（问题解决）如图2，在等边三角形ABC内有一点P，且PA＝2，PB＝ ，PC＝1，求∠BPC的度数和等边三角形ABC的边长；
(3)、（灵活运用）如图3，在正方形ABCD内有一点P，且PA＝ ，BP＝ ，PC＝1，求∠BPC的度数．