2023年中考数学精选真题实战测试23 反比例函数 A
试卷更新日期:2023-01-13 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 在平面直角坐标系中,反比例函数的图象如图所示,则一次函数的图象经过的象限是( )
 A、一、二、三 B、一、二、四 C、一、三、四 D、二、三、四2. 如图,正比例函数与反比例函数的图象交于、B两点,当时,x的取值范围是( )
A、一、二、三 B、一、二、四 C、一、三、四 D、二、三、四2. 如图,正比例函数与反比例函数的图象交于、B两点,当时,x的取值范围是( ) A、或 B、或 C、或 D、或3. 在同一平面直角坐标系中,函数y=ax+b与(其中a,b是常数,ab≠0)的大致图象是( )A、
A、或 B、或 C、或 D、或3. 在同一平面直角坐标系中,函数y=ax+b与(其中a,b是常数,ab≠0)的大致图象是( )A、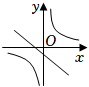 B、
B、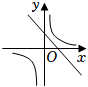 C、
C、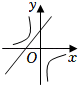 D、
D、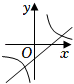 4. 如图,在函数 的图象上任取一点A,过点A作y轴的垂线交函数 的图象于点B,连接OA,OB,则 的面积是( )
4. 如图,在函数 的图象上任取一点A,过点A作y轴的垂线交函数 的图象于点B,连接OA,OB,则 的面积是( )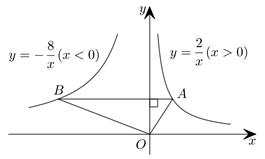 A、3 B、5 C、6 D、105. 如图,矩形OABC与反比例函数(k1是非零常数,x>0)的图象交于点M,N,与反比例函数(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1-k2=( )
A、3 B、5 C、6 D、105. 如图,矩形OABC与反比例函数(k1是非零常数,x>0)的图象交于点M,N,与反比例函数(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1-k2=( )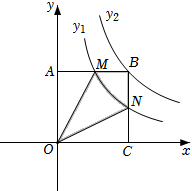 A、3 B、-3 C、 D、6. 一次函数y=mx+n的图象与反比例函数y= 的图象交于点A、B,其中点A、B的坐标为A(- ,-2m)、B(m,1),则△OAB的面积( )A、3 B、 C、 D、7. 如图,在平面直角坐标系中,点O为坐标原点,平行四边形OBAD的顶点B在反比例函数的图象上,顶点A在反比例函数的图象上,顶点D在x轴的负半轴上.若平行四边形OBAD的面积是5,则k的值是( )
A、3 B、-3 C、 D、6. 一次函数y=mx+n的图象与反比例函数y= 的图象交于点A、B,其中点A、B的坐标为A(- ,-2m)、B(m,1),则△OAB的面积( )A、3 B、 C、 D、7. 如图,在平面直角坐标系中,点O为坐标原点,平行四边形OBAD的顶点B在反比例函数的图象上,顶点A在反比例函数的图象上,顶点D在x轴的负半轴上.若平行四边形OBAD的面积是5,则k的值是( )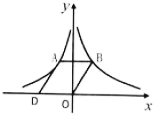 A、2 B、1 C、 D、8. 如图,正方形 的顶点分别在反比例函数 和 的图象上.若 轴,点 的横坐标为3,则 ( )
A、2 B、1 C、 D、8. 如图,正方形 的顶点分别在反比例函数 和 的图象上.若 轴,点 的横坐标为3,则 ( )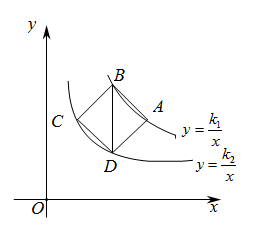 A、36 B、18 C、12 D、99. 呼气式酒精测试仪中装有酒精气体传感器,可用于检测驾驶员是否酒后驾车.酒精气体传感器是一种气敏电阻(图1中的 ), 的阻值随呼气酒精浓度K的变化而变化(如图2),血液酒精浓度M与呼气酒精浓度K的关系见图3.下列说法不正确的是( )
A、36 B、18 C、12 D、99. 呼气式酒精测试仪中装有酒精气体传感器,可用于检测驾驶员是否酒后驾车.酒精气体传感器是一种气敏电阻(图1中的 ), 的阻值随呼气酒精浓度K的变化而变化(如图2),血液酒精浓度M与呼气酒精浓度K的关系见图3.下列说法不正确的是( ) A、呼气酒精浓度K越大, 的阻值越小 B、当K=0时, 的阻值为100 C、当K=10时,该驾驶员为非酒驾状态 D、当 时,该驾驶员为醉驾状态10. 在平面直角坐标系中,为坐标原点,已知点、(且),过点、的直线与两坐标轴相交于、两点,连接、 , 则下列结论中成立的是( )
A、呼气酒精浓度K越大, 的阻值越小 B、当K=0时, 的阻值为100 C、当K=10时,该驾驶员为非酒驾状态 D、当 时,该驾驶员为醉驾状态10. 在平面直角坐标系中,为坐标原点,已知点、(且),过点、的直线与两坐标轴相交于、两点,连接、 , 则下列结论中成立的是( )①点、在反比例函数的图象上;②成等腰直角三角形;③;④的值随的增大而增大.
A、②③④ B、①③④ C、①②④ D、①②③二、填空题(每空3分,共18分)
-
11. 科技小组为了验证某电路的电压U(V)、电流I(A)、电阻 三者之间的关系: ,测得数据如下:
100
200
220
400
2.2
1.1
1
0.55
那么,当电阻 时,电流 A.
12. 在平面直角坐标系中,将点向下平移5个单位长度得到点 , 若点恰好在反比例函数的图象上,则的值是.13. 如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD, , 则k= .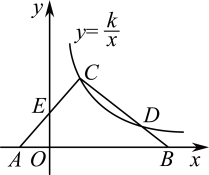 14. 如图四边形ABCD是平行四边形,CD在x轴上,点B在y轴上,反比例函数的图象经过第一象限点A,且平行四边形ABCD的面积为6,则 .
14. 如图四边形ABCD是平行四边形,CD在x轴上,点B在y轴上,反比例函数的图象经过第一象限点A,且平行四边形ABCD的面积为6,则 .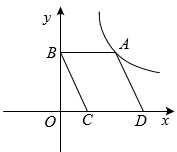 15. 如图,A,B是双曲线y=(x>0)上的两点,连接OA,OB.过点A作AC⊥x轴于点C,交OB于点D.若D为AC的中点,△AOD的面积为3,点B的坐标为(m,2),则m的值为 .
15. 如图,A,B是双曲线y=(x>0)上的两点,连接OA,OB.过点A作AC⊥x轴于点C,交OB于点D.若D为AC的中点,△AOD的面积为3,点B的坐标为(m,2),则m的值为 .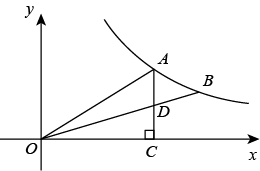 16. 如图,正方形OABC的顶点A、C分别在x轴和y轴上,E、F分别是边AB、OA上的点,且∠ECF=45°,将△ECF沿着CF翻折,点E落在x轴上的点D处.已知反比例函数y1=和y2=分别经过点B、点E,若S△COD=5,则k1﹣k2= .
16. 如图,正方形OABC的顶点A、C分别在x轴和y轴上,E、F分别是边AB、OA上的点,且∠ECF=45°,将△ECF沿着CF翻折,点E落在x轴上的点D处.已知反比例函数y1=和y2=分别经过点B、点E,若S△COD=5,则k1﹣k2= .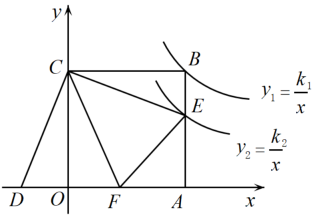
三、解答题(共8题,共72分)
-
17. 如图,一次函数的图象与反比例函数的图象交于A、B两点,求的面积.
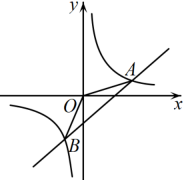 18. 一个一次函数的截距为1,且经过点A(2,3).(1)、求这个一次函数的解析式;(2)、点A,B在某个反比例函数上,点B横坐标为6,将点B向上平移2个单位得到点C,求cos∠ABC的值.19. 如图,一次函数与反比例函数的图象交于点 , 与轴交于点 .
18. 一个一次函数的截距为1,且经过点A(2,3).(1)、求这个一次函数的解析式;(2)、点A,B在某个反比例函数上,点B横坐标为6,将点B向上平移2个单位得到点C,求cos∠ABC的值.19. 如图,一次函数与反比例函数的图象交于点 , 与轴交于点 .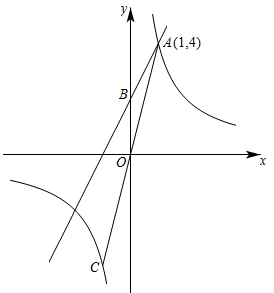 (1)、 , ;(2)、连接并延长 , 与反比例函数的图象交于点 , 点在轴上,若以、、为顶点的三角形与相似,求点的坐标.20. 如图,一次函数的图象与轴、轴分别相交于、两点,与反比例函数的图象相交于点 , , , :: .
(1)、 , ;(2)、连接并延长 , 与反比例函数的图象交于点 , 点在轴上,若以、、为顶点的三角形与相似,求点的坐标.20. 如图,一次函数的图象与轴、轴分别相交于、两点,与反比例函数的图象相交于点 , , , :: .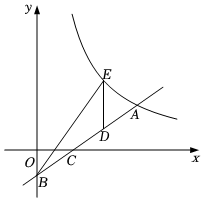 (1)、求反比例函数的表达式;(2)、点是线段上任意一点,过点作轴平行线,交反比例函数的图象于点 , 连接当面积最大时,求点的坐标.21. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象相交于 , 两点.
(1)、求反比例函数的表达式;(2)、点是线段上任意一点,过点作轴平行线,交反比例函数的图象于点 , 连接当面积最大时,求点的坐标.21. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象相交于 , 两点. (1)、求一次函数和反比例函数的解析式;(2)、若点 在 轴上,位于原点右侧,且 ,求 的面积.22. 如图,一次函数的图象与反比例函数的图象交于点和点 .
(1)、求一次函数和反比例函数的解析式;(2)、若点 在 轴上,位于原点右侧,且 ,求 的面积.22. 如图,一次函数的图象与反比例函数的图象交于点和点 .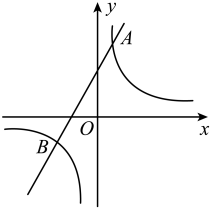 (1)、求一次函数的表达式;(2)、结合图象,写出当时,满足的x的取值范围;(3)、将一次函数的图象平移,使其经过坐标原点.直接写出一个反比例函数表达式,使它的图像与平移后的一次函数图象无交点.23. 如图,在平面直角坐标系中,直线与轴、轴分别交于点、两点,与双曲线交于点、两点, .
(1)、求一次函数的表达式;(2)、结合图象,写出当时,满足的x的取值范围;(3)、将一次函数的图象平移,使其经过坐标原点.直接写出一个反比例函数表达式,使它的图像与平移后的一次函数图象无交点.23. 如图,在平面直角坐标系中,直线与轴、轴分别交于点、两点,与双曲线交于点、两点, .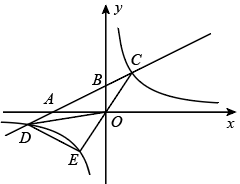 (1)、求 , 的值;(2)、求点坐标并直接写出不等式的解集;(3)、连接并延长交双曲线于点 , 连接、 , 求的面积.24. 某市在盐碱地种植海水稻获得突破性进展,小亮和小莹到海水稻种植基地调研.小莹根据水稻年产量数据,分别在直角坐标系中描出表示2017-2021年①号田和②号田年产量情况的点(记2017年为第1年度,横轴表示年度,纵轴表示年产量),如下图.
(1)、求 , 的值;(2)、求点坐标并直接写出不等式的解集;(3)、连接并延长交双曲线于点 , 连接、 , 求的面积.24. 某市在盐碱地种植海水稻获得突破性进展,小亮和小莹到海水稻种植基地调研.小莹根据水稻年产量数据,分别在直角坐标系中描出表示2017-2021年①号田和②号田年产量情况的点(记2017年为第1年度,横轴表示年度,纵轴表示年产量),如下图.
小亮认为,可以从y=kx+b(k>0) ,y=(m>0) ,y=−0.1x2+ax+c中选择适当的函数模型,模拟①号田和②号田的年产量变化趋势.
(1)、小莹认为不能选 . 你认同吗?请说明理由;(2)、请从小亮提供的函数模型中,选择适当的模型分别模拟①号田和②号田的年产量变化趋势,并求出函数表达式;(3)、根据(2)中你选择的函数模型,请预测①号田和②号田总年产量在哪一年最大?最大是多少?