2023年浙教版数学七年级下册全方位训练卷第二章二元一次方程组（进阶版）

试卷更新日期：2023-01-12 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 若 $x^{| m - 2 |}$ +（m-1）y=6是关于x，y的二元一次方程，则m的值是（）

A、3 B、1 C、任意数 D、1或3

查看试题解析
2. 若 ${\begin{array}{l} x = 1 \\ y = 0 \end{array}$ 是二元一次方程 $a x + y = 3$ 的一个解，则下列x，y的值也是该方程的解的是（）

A、 ${\begin{array}{l} x = 0 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = 0 \\ y = 3 \end{array}$ C、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = 0 \end{array}$

查看试题解析
3. 使方程组 ${\begin{cases} 2 x + m y = 16 \\ x - 2 y = 0 \end{cases}$ 有自然数解的整数m（）

A、只有5个 B、只能是偶数 C、是小于16的自然数 D、是小于32的自然数

查看试题解析
4. 已知 $∠ A$ 、 $∠ B$ 互补， $∠ A$ 比 $∠ B$ 小 $30 °$ ，设 $∠ A$ 、 $∠ B$ 的度数分别为 $x °$ 、 $y °$ ，下列方程组中正确的是（）

A、 ${\begin{array}{l} x + y = 180 \\ x = y - 30 \end{array}$ B、 ${\begin{array}{l} x + y = 180 \\ x = y + 30 \end{array}$ C、 ${\begin{array}{l} x + y = 90 \\ x = y + 30 \end{array}$ D、 ${\begin{array}{l} x + y = 90 \\ x = y - 30 \end{array}$

查看试题解析
5. 若a、b、c、d是正整数，且a+b＝20，a+c＝24，a+d＝22，设a+b+c+d的最大值为M，最小值为N，则M﹣N＝（）

A、28 B、12 C、48 D、36

查看试题解析
6. 我国古代数学家张丘建在《张丘建算经）里，提出了“百钱买百鸡”这个有名的数学问题.用100个钱买100只鸡，公鸡每只五个钱，母鸡每只三个钱，小鸡每个钱三只.问公鸡，小鸡各买了多少只？在这个问题中，小鸡的只数不可能是（）

A、87 B、84 C、81 D、78

查看试题解析
7. 已知关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} x + y = - a + 1 \\ x - y = 3 a + 5 \end{array}$ ，给出下列说法：①当 $a = 0$ 时，方程组的解也是方程 $2 x + y = 4$ 的一个解；②当 $x - 2 y > 7$ 时， $a > 0$ ；③不论 $a$ 取什么实数， $2 x + y$ 的值始终不变；④若 $a = 1$ ，则 $x^{2} + 4 y = 0$ 以上四种说法中正确的有（）个

A、1 B、2 C、3 D、4

查看试题解析
8. 一道来自课本的习题：
从甲地到乙地先有一段上坡路后有一段平路．如果保持上坡每小时走3km，平路每小时走4km，下坡每小时走5km，那么从甲地到乙地需54分钟，从乙地到甲地需42分钟，甲地到乙地全程是多少？
小红将这个实际问题转化为二元一次方程组问题，采用间接设法：
设坡路有x km，平路有y km，则全程为（x＋y）km．已经列出一个方程 $\frac{x}{3} + \frac{y}{4} = \frac{54}{60}$ ，则另一个方程正确的是（）

A、 $\frac{x}{4} + \frac{y}{3} = \frac{42}{60}$ B、 $\frac{x}{5} + \frac{y}{4} = \frac{42}{60}$ C、 $\frac{x}{4} + \frac{y}{5} = \frac{42}{60}$ D、 $\frac{x}{3} + \frac{y}{4} = \frac{42}{60}$

查看试题解析
9. 将两块完全相同的长方体木块先按图1的方式放置，再按图2的方式放置，测得的数据如图所示．则桌子的高度 $h =$ （）

A、70 B、55 C、40 D、30

查看试题解析
10. 如图，长青化工厂与 $A$ ， $B$ 两地有公路、铁路相连．这家工厂从 $A$ 地购买一批每吨1000元的原料运回工厂，制成每吨6000元的产品运到 $B$ 地．公路运价为1.6元 $/ (t • k m)$ ，铁路运价为1.2元 $/ (t • k m)$ ，这两次运输共支出公路运费16000元，铁路运费97200元．这批产品的销售款比原料费与运输费的和多（）元．

A、1286800 B、299000 C、1286000 D、298000

查看试题解析

二、填空题（每题3分，共15分）

11. 小亮解方程组 ${\begin{array}{l} 2 x + y = 0 \\ 2 x - y = ● \end{array}$ 的解为 ${\begin{array}{l} x = 5 \\ y = ★ \end{array}$ ，由于不小心，滴上了两滴墨水，刚好遮住了两个数●和★，请你帮他找回★和●，这个数★＝， ●＝.

查看试题解析
12. 若关于x ， y的 ${\begin{matrix} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{matrix}$ 的解是 ${\begin{matrix} x = 2 \\ y = - 3 \end{matrix}$ ，则关于m ， n的方程组 ${\begin{matrix} 2 a_{1} (m - n) - 3 b_{1} (m + n) = 5 c_{1} \\ 2 a_{2} (m - n) - 3 b_{2} (m + n) = 5 c_{2} \end{matrix}$ 的解是．

查看试题解析
13. 为迎接建国70周年，某商店购进 $A$ ， $B$ ， $C$ 三种纪念品共若干件，且 $A$ ， $B$ ， $C$ 三种纪念品的数量之比为8：7：9，一段时间后，根据销售情况，补充三种纪念品后，库存总数量比第一次多200件，且 $A$ ， $B$ ， $C$ 三种纪念品的比例为9：10：10，又一段时间后，根据销售情况，再次补充三种纪念品，库存总数景比第二次多170 件，且 $A$ ， $B$ ， $C$ 三种纪念品的比例为7： 6： 6，已知第一次三种纪念品总数盘不超过1000件，则第一次购进 $A$ 种纪念品件.

查看试题解析
14. 如图，两个形状、大小完全相同的大长方形内放入四个如图③的小长方形后分别得到如图①、图②、已知大长方形的长为a，则图②阴影部分周长与图①阴影部分周长的差是．

查看试题解析
15. 小明在拼图时，发现8个一样大小的长方形如图1那样，恰好可以拼成一个大的长方形．小红看见了，说：“我来试一试．”结果小红七拼八凑，拼成如图2那样的正方形．“咳，怎么中间还留了一个洞，恰好是边长为 $2 m m$ 的小正方形 $！$ ”请你写出这些长方形的长和宽．

查看试题解析

三、计算题（共8分）

16. 解方程组

(1)、 ${\begin{matrix} y = x + 3 \\ 7 x + 5 y = 9 \end{matrix}$ ；

(2)、 ${\begin{matrix} 3 x + 2 y = 5 \\ 3 x - 5 y = - 2 \end{matrix}$

(3)、 ${\begin{matrix} 5 x + 5 y = 12 \\ 2 x + 3 y = 7 \end{matrix}$ ；

(4)、 ${\begin{matrix} x + y = 13 \\ y + z = 5 \\ x + z = 4 \end{matrix}$

查看试题解析

四、解答题（共8题，共67分）

17. 关于x，y的二元一次方程ax+by＝c（a，b，c是常数），b＝a+1，c＝b+1.

(1)、当 ${\begin{cases} x = 3 \\ y = 1 \end{cases}$ 时，求c的值.

(2)、当a＝ $\frac{1}{2}$ 时，求满足|x|＜5，|y|＜5的方程的整数解.

(3)、若a是正整数，求证：仅当a＝1时，该方程有正整数解.

查看试题解析
18. 已知关于x，y的二元一次方程组 ${\begin{cases} x - y = 3 - a \\ x + 2 y = 5 a \end{cases}$ （a为实数）．

(1)、若方程组的解始终满足y=a+1，求a的值．

(2)、已知方程组的解也是方程bx+3y=1(b为实数，b≠0且b≠-6)的解．
①探究实数a，b满足的关系式．

②若a，b都是整数，求b的最大值和最小值．

查看试题解析
19.

(1)、阅读下列材料并填空：
对于二元一次方程组 ${\begin{matrix} 4 x + 3 y = 54 ， \\ x + 3 y = 36 ， \end{matrix}$ 我们可以将x，y的系数和相应的常数项排成一个数表 $(\begin{array}{r} 4 & 3 & 54 \\ 1 & 3 & 36 \end{array})$ ，求得的一次方程组的解 ${\begin{matrix} x = a ， \\ y = b \end{matrix}$ 用数表可表示为 $(\begin{array}{r} 1 & 0 & a \\ 0 & 1 & b \end{array})$ .用数表可以简化表达解一次方程组的过程如下，请补全其中的空白：
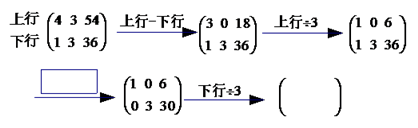
从而得到该方程组的解为 ${\begin{matrix} x =__， \\ y =__. \end{matrix}$

(2)、仿照（1）中数表的书写格式写出解方程组 ${\begin{matrix} 2 x + 3 y = 6 ， \\ x + y = 2 \end{matrix}$ 的过程．

查看试题解析
20. 已知关于x，y的方程组 ${\begin{cases} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{cases}$ 的解是 ${\begin{cases} x = 4 \\ y = - 6 \end{cases}$

(1)、若把x换成m，y换成n，得到的关于m，n的方程组为 ${\begin{cases} a_{1} m + b_{1} n = c_{1} \\ a_{2} m + b_{2} n = c_{2} \end{cases}$ ，则这个方程组的解是 ${\begin{cases} m =_______ \\ n =_______ \end{cases}$ .

(2)、若把x换成2x，y换成3y，得到方程组 ${\begin{cases} 2 a_{1} x + 3 b_{1} y = c_{1} \\ 2 a_{2} x + 3 b_{2} y = c_{2} \end{cases}$ ，则 ${\begin{cases} 2 x =_______ \\ 3 y =_______ \end{cases}$ ，所以这个方程组的解是 .

(3)、根据以上的方法解方程组 ${\begin{cases} 2 a_{1} x - b_{1} y = 5 c_{1} \\ 2 a_{2} x - b_{2} y = 5 c_{2} \end{cases}$

查看试题解析
21. 阅读下列材料：
小明同学遇到下列问题：解方程组 ${\begin{array}{l} \frac{2 x + 3 y}{4} + \frac{2 x - 3 y}{3} = 7 \\ \frac{2 x + 3 y}{3} + \frac{2 x - 3 y}{2} = 8 \end{array}$ 小明发现如果用代入消元法或加减消元法求解，运算量比较大，容易出错．如果把方程组中的（2x+3y）看成一个整体，把（2x﹣3y）看成一个整体，通过换元，可以解决问题．以下是他的解题过程：令m＝2x+3y，n＝2x﹣3y．原方程组化为 ${\begin{array}{l} \frac{m}{4} + \frac{n}{3} = 7 \\ \frac{m}{3} + \frac{n}{2} = 8 \end{array}$ ，解的 ${\begin{array}{l} m = 60 \\ n = - 24 \end{array}$ ，把 ${\begin{array}{l} m = 60 \\ n = - 24 \end{array}$ 代入m＝2x+3y，n＝2x﹣3y，得 ${\begin{array}{l} 2 x + 3 y = 60 \\ 2 x - 3 y = - 24 \end{array}$ 解得 ${\begin{array}{l} x = 9 \\ y = 14 \end{array}$ 所以，原方程组的解为 ${\begin{array}{l} x = 9 \\ y = 14 \end{array}$ ．
请你参考小明同学的做法解方程组：

(1)、 ${\begin{array}{l} \frac{x + y}{6} + \frac{x - y}{10} = 3 \\ \frac{x + y}{6} - \frac{x - y}{10} = - 1 \end{array}$ ；

(2)、 ${\begin{array}{l} \frac{5}{x} + \frac{2}{y} = 11 \\ \frac{3}{x} - \frac{2}{y} = 13 \end{array}$ ．

查看试题解析
22. 文雅书店出售A，B两种书籍，已知A书籍单售为每本50元，B书籍单售为每本30元，整套(A，B各一本)出售为每套70元。

(1)、小明购买了A，B两种书籍共20本，且购买的B书籍数量比A书籍数量的2倍少4本。
①小明购买了A，B两种书籍各多少本？

②小明至少需要花费多少钱？

(2)、如果小刚花了600元购买A，B两种书籍，其中A书籍购买了8本，那么有哪几种购买方案？其中哪一种方案最划算？

查看试题解析
23. 某校举办“迎冬奥会“学生书画展览，现要在长方形展厅中划出3个形状、大小完全一样的小长方形(图中阴影部分)区域摆放作品．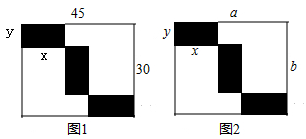

(1)、如图1，若大长方形的长和宽分别为45米和30米，设小长方形的长为x，宽为y，求出x和y的值．

(2)、如图2，若大长方形的长和宽分别为a和b．
①求出1个小长方形周长与大长方形周长之比；

②若作品展览区域(阴影部分)面积占展厅面积的 $\frac{1}{3}$ ，求x和y的数量关系．

查看试题解析
24. 某包装生产企业承接了一批礼品盒制作业务，为了确保质量，该企业进行试生产.他们购得规格是170cm×40cm的标准板材作为原材料，每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材（不计损耗），如图1.（单位：cm）

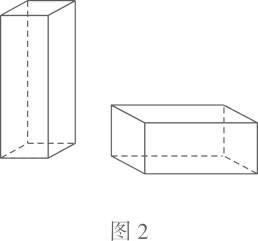(1)、列出方程（组），求出图1中a与b的值；

(2)、在试生产阶段，若将30张标准板材用裁法一裁剪，4张标准板材用裁法二裁剪，再将得到的A型与B型板材做侧面和底面，做成图2的竖式（高大于长）与横式（长大于高）两种无盖礼品盒.
①两种裁法共生产A型板材 ▲ 张，B型板材 ▲ 张.

②能否在做成若干个上述的两种无盖礼品盒后，恰好把①中的A型板材和B型板材用完？若能，则竖式无盖礼品盒与横式无盖礼品盒分别做了几个？若不能，则最多能做成竖式和横式两种无盖礼品盒共多少个？并直接写出此时做成的横式无盖礼品盒的个数.

查看试题解析

2023年浙教版数学七年级下册全方位训练卷第二章 二元一次方程组（进阶版）

一、单选题（每题3分，共30分）

二、填空题（每题3分，共15分）

三、计算题（共8分）

四、解答题（共8题，共67分）

2023年浙教版数学七年级下册全方位训练卷第二章二元一次方程组（进阶版）