2023年浙教版数学七年级下册全方位训练卷2.5三元一次方程组及其解法
试卷更新日期：2023-01-12 类型：同步测试
一、单选题（每题3分，共30分）
-
1. 方程组 的解是（ ）A、 B、 C、 D、2. 解方程组
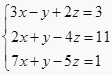，若要使计算简便，消元的方法应选取（ ） A、先消去x B、先消去y C、先消去z D、以上说法都不对3. 若实数 满足 ，则 （ ）A、 B、 C、 D、不能确定值4. 用“●”“■”“▲”分别表示三种不同的物体，如图所示，前两架天平保持平衡，若要使第三架天平也平衡，那么“？”处应放“■”的个数为（ ）
A、5 B、4 C、3 D、25. 6月18日最开始是京东的周年庆，相当于淘宝的双十一活动，在2013年之前，京东就将每年的6月18日定为年庆。2013年后，618就成了各大电商平台的网购节了。在618当日，小李在某电商平台上选择了甲乙丙三种商品，当购物车内选3件甲，2件乙，1件丙时显示价格为420元；当选2件甲，3件乙，4件丙时显示价格为580元，那么购买甲、乙、丙各一件时应该付款（ ）A、580元 B、500元 C、420元 D、200元6. 已知买20支铅笔、3块橡皮、2本日记本共需32元，买39支铅笔、5块橡皮、3本日记本共需58元，则购买10支铅笔、10块橡皮与10本日记本共需（ ）元A、16 B、60 C、30 D、667. 甲、乙、丙三种商品，若购买甲2件、乙4件、丙3件，共需220元钱，购甲3件、乙1件、丙2件共需235元钱，那么购甲、乙、丙三种商品各一件共需（ ）A、85元 B、89元 C、90元 D、91元8. 如图，已知两个天平都处于平衡状态，那么四个小球的重量等同于小正方体的个数为（ ）
A、15个 B、14个 C、13个 D、12个9. 小明妈妈到文具店购买三种学习用品，其单价分别为2元、4元、6元，购买这些学习用品需要56元，经过协商最后以每种单价均下调0.5元成交，结果只用了50元就买下了这些学习用品，则小明妈妈有几种不同的购买方法.（ ）A、6 B、5 C、4 D、310. 为确保信息安全，信息需要加密传输，发送方由明文→密文（加密）（解密），接收方由密文→明文（解密），已知加密规则为：明文a，b，c，对应密文a+1，-a+2b+4，b+3c+9，如果接收方收到密文7，12，22，则解密得到的明文为（ ）A、6，2，7 B、2，6，7 C、6，7，2 D、7，2，6二、填空题（每题4分，共24分）
-
11. 实数x，y，z满足2x+y-3z=5，x+2y+z=-4，请用含x的代数式表示z，即.12. 有一片牧场，草每天都在匀速地生长（即草每天增长的量相等），如果放牧24头牛，则6天吃完牧草；如果放牧21头牛，则8天吃完牧草.设每头牛每天吃草的量是相等的，如果放牧16头牛，则天可以吃完牧草.13. 中午放学后，有a个同学在学校一食堂门口等候进食堂就餐，由于二食堂面积较大，所以配餐前二食堂等待就餐的学生人数是一食堂的2倍，开始配餐后，仍有学生继续前来排队等候就餐，设一食堂排队的学生人数按固定的速度增加，且二食堂学生人数增加的速度是一食堂的2倍，两个食堂每个窗口阿姨配餐的速度是一样的，一食堂若开放12个配餐窗口，则需10分钟才可为排队就餐的同学配餐完毕；二食堂若开放20个配餐窗口，则14分钟才可为排队就餐的同学配餐完毕；若需要在15分钟时刚好配餐完毕，则两个食堂需要同时一共开放个配餐窗口.14. 如图，每条边上的三个数之和都等于16，么a ， b ， c这三个数按顺序分别为 ．
15. “洞庭碧螺春，品香醉天下.”洞庭碧螺春产于苏州市太湖洞庭山，以形美、色艳、香浓、味醇“四绝”驰名中外.如图，若将一壶碧螺春茶倒满2个小杯，则还剩 壶；若倒满1个小杯后再全部倒入1个大杯中，则只能倒满这个大杯的 .1个小杯与1个大杯的容积之比为.
16. 端午节有吃粽子的习惯，某商店购进肉粽、蛋黄粽、豆沙粽的数量之比为 .为促进销售，将全部粽子包装成A、B、C三种礼盒.礼盒A有2个肉粽、4个蛋黄粽；礼盒B有1个肉粽、3个蛋黄粽、1个豆沙粽；礼盒C有4个肉粽、2个豆沙粽.则礼盒A、礼盒B、礼盒C的盒数之比为.三、解答题（共8题，共66分）
-
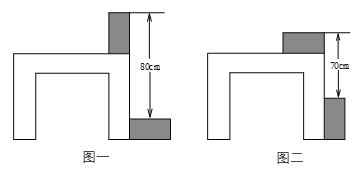
17. 解三元一次方程组：18. 在等式y＝ax2+bx+c中，当x＝﹣1时，y＝3；当x＝0时，y＝1，当x＝1时，y＝1，求这个等式中a、b、c的值.19. 有三个数，第一个数的3倍比第二个数的5倍小90，而第一个数的4倍与第二个数的6倍之差等于第三个数的20倍的相反数，同时，第三个数比4大1．求这三个数．20. 利用两块完全相同的长方形木块测量一张桌子的高度，首先将木块按图一方式放置，再交换两木块的位置，按图二方式放置，测量数据如图，求桌子的高度.
21. 阅读材料：善于思考的小明在解方程组 时，采用了一种“整体代换”的解法，解法如下：解：将方程②8x+20y+2y=10，变形为 2（4x+10y）+2y=10③，把方程①代入③得，2×6+2y=10，则 y=﹣1；把 y=﹣1 代入①得，x=4，所以方程组的解为： 请你解决以下问题：
(1)、试用小明的“整体代换”的方法解方程组(2)、已知 x、y、z，满足 试求 z 的值.22. 【信息阅读】有些问题，所要求的结果往往不是某一个量的值，而是某些式子或问题的整体值.
如下面的问题：
问题：已知实数x，y同时满足3x- y =5①，和2x+3y =7②．求代数式7x+5y的值.
思路1：将①和②联立组成方程组，先求得x、y的值后，再代入7x +5y求值.
思路2：为降低运算量，由①+②×2，可直接得出7x+5y = 19．这样的解题思路即为整体思想.
【问题解决】
(1)、已知方程组 ， 则x- y =；(2)、若购买13支铅笔、5块橡皮、3本日记本共需33元；若购买25支铅笔、9块橡皮、3本日记本共需55元，求购买1支铅笔、1块橡皮、3本日记本共需多少元?23. 水果市场将120吨水果运往各地商家，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如表所示：（假设每辆车均满载）车型
甲
乙
丙
汽车运载量（吨/辆）
5
8
10
汽车运费（元/辆）
400
500
600
(1)、若全部水果都用甲、乙两种车型来运送，需运费8200元，问分别需甲、乙两种车型各几辆？(2)、为了节约运费，市场可以调用甲、乙、丙三种车型参与运送（每种车型至少1辆），已知它们的总辆数为16辆，如何安排车辆运送使总运费最省？24. 有一场足球比赛，共有九支球队参加，采取单循环赛，其记分和奖励方案如下表：标准
胜一场
平一场
负一场
积分
3
1
0
奖励（元／人）
2000
800
0
甲队参加完了全部8场比赛，共得积分16分．
(1)、求甲队胜负的所有可能情况；(2)、若每一场比赛，每一个参赛队员均可得出场费500元，求甲队参加了所有8场比赛的队员的个人总收入（奖金加上出场费）．