2023年浙教版数学七年级下册全方位训练卷第一章 平行线（进阶版）
试卷更新日期：2023-01-12 类型：单元试卷
一、单选题（每题3分，共30分）
-
1. 下列语句正确的个数是（ ）
⑴经过平面内一点有且只有一条直线与已知直线垂直；
⑵经过平面内一点有且只有一条直线与已知直线平行；
⑶在同一平面内，如果两条直线都与第三条直线平行，那么这两条直线也互相平行；
⑷在同一平面内，如果两条直线都与第三条直线垂直，那么这两条直线也互相平行．
A、1个 B、2个 C、3个 D、4个2. 三条直线相交，交点最多有（ ）A、1个 B、2个 C、3个 D、4个3. 如图，给出下列说法：①∠B和∠1是同位角；②∠1和∠3是对顶角；③∠2和∠4是内错角；④∠A和∠BCD是同旁内角．其中说法正确的有（ ）
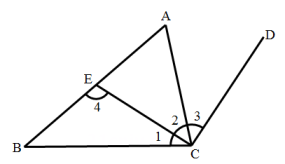A、0个 B、1个 C、2个 D、3个4. 下列说法正确的有（ ）①对顶角相等；②同位角相等；③若两个角不相等，则这两个角一定不是对顶角；④若两个角不相等，则这两个角一定不是同位角.
A、1个 B、2个 C、3个 D、4个5. 如图.在下列条件中，不能推出的是（ ）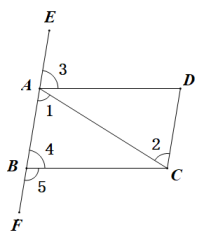
A、∠3＝∠4 B、∠1＝∠2 C、∠4＋∠BCD＝180°，且∠D＝∠4 D、∠3＋∠5＝180°6. 一副直角三角尺叠放如图1所示，现将含 角的三角尺ADE固定不动，将含 角的三角尺ABC绕顶点 顺时针转动，使两块三角尺至少有一组边互相平行，如图2，当 时， ，则 )其他所有可能符合条件的度数为（ ）
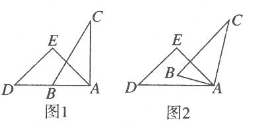A、 和 B、 和 C、 和 D、以上都有可能7. 如图：有、、三户家用电路接入电表，相邻电路的接点距离相等，相邻电表的距离相等，且相邻电路的接点距离等于相邻电表接入点的距离，电线对应平行排列，则三户所用电线（ ）
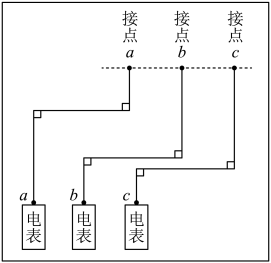A、户最长 B、户最长 C、户最长 D、三户一样长8. 如图，已知直线AB，CD被直线AC所截，AB∥CD，E是平面内任意一点（点E不在直线AB，CD，AC上），设∠BAE=α，∠DCE=β．下列各式：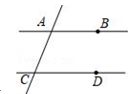
①α+β，②α﹣β，③β﹣α，④360°﹣α﹣β，∠AEC的度数可能是（ ）
A、①②③ B、①②④ C、①③④ D、①②③④ 图49. 已知：如图，点D是射线AB上一动点，连接CD，过点D作DE∥BC交直线AC于点E，若∠ABC=84°，∠CDE=20°，则∠ADC的度数为（ ）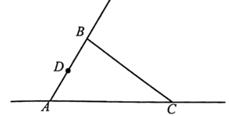
A、104° B、76° C、104°或64° D、104°或76°10. 如图，长方形ABCD中，AB＝8，第一次平移长方形ABCD沿AB的方向向右平移6个单位，得到长方形A1B1C1D1 ， 第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移6个单位，得到长方形A2B2C2D2 ， ……第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1的方向平移6个单位，得到长方形AnBn∁nDn（n＞2），若ABn的长度为2018，则n的值为（ ）
A、334 B、335 C、336 D、337二、填空题（第11题4分，12-16题2分，共14分）
-
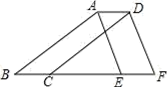
11. n条水平直线与倾斜直线a相交可得条线段，对同位角，对内错角，对同旁内角．12. 平面内两两相交的三条直线，如果它们最多有a个交点，最少有b个交点，则a+b＝ ．13. 如图，将三角形ABE向右平移1cm得到三角形DCF，如果三角形ABE的周长是10cm，那么四边形ABFD的周长是 ．
14. 如图，直线AB//CD，点M、N分别在直线AB、CD上，点E为直线AB与CD之间的一点，连接ME、NE，且∠MEN=80°，∠AME的角平分线与∠CNE的角平分线交于点F，则∠MFN的度数为 ．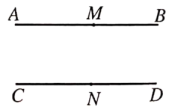
15. 一副直角三角尺如图①叠放，现将45°的三角尺ADE固定不动，将含30°的三角尺ABC绕顶点A顺时针转动，要求两块三角尺的一组边互相平行.如图②，当∠BAD=15°时，有一组边BC∥DE，请再写出两个符合要求的∠BAD（0°＜∠BAD＜180°）的度数.
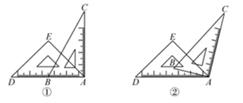16. 在间一平面内，有2019条互不重合的直线，l1 ， l2 ， l3 ， …，l2019 ， 若l1⊥l2 ， l2∥l3 ， l3⊥l4 ， l4∥l5 ， 以此类推，则l1和l2019的位置关系是.三、作图题（共6分）
-
17. 如图，已知锐角∠AOB，M，N分别是∠AOB两边OA，OB上的点，用直尺或三角板按下列要求画图：
（ 1 ）过点M作OB的垂线段MC，C为垂足；
（ 2 ）过点N作OA的平行线ND；
（ 3 ）平移△OMC，使点M移动到点N处，画出平移后的△ENF，其中E，F分别为点O，C的对应点．
18. 如图，方格纸上每个小正方形的边长均为1个单位长度，点A，B，C都在格点上（两条网格线的交点叫格点）.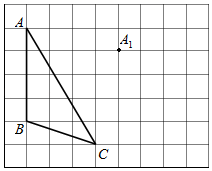
(1)、①平移 ABC，使点A移动到点A1 ， 请在网格纸上画出平移后的 A1B1C1；
②作 ABC的高CE；(2)、在（1）的条件下，求平移过程中，线段AB扫过的面积.四、解答题（共8题，共64分）
-
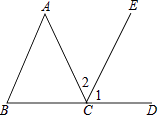
19. 如图，BCD是一条直线，∠1=∠B，∠2=∠A，指出∠1的同位角，∠2的内错角，并求出∠A+∠B+∠ACB的度数．
20. 如图，在折线中，已知 ， 延长、交于点 ， 猜想与的关系，并说明理由．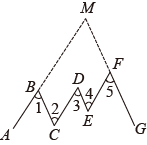
21. 如图为一梯级平面图，一只老鼠沿长方形的两边 的路线逃跑，一只猫同时沿梯级 折线 的路线追，结果在距离C点 的D点处，猫捉住了老鼠，已知老鼠的速度是猫的 ，求梯级 折线 的长度，
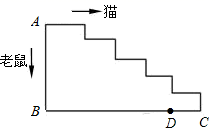(1)、请将下表中每一句话“译成”数学语言 在表格中写出对应的代数式 ：设梯级 折线 的长度为
xm
的长度为
的长度为
的长度为
设猫捉住老鼠所用时间为
ts
猫的速度是
老鼠的速度是
(2)、根据表格中代数式列出一个你认为正确的方程 不要求解 ：.22. 如图，AB、CD被AC所截，AB∥CD，∠CAB＝108°，点P为直线AB上一动点（不与点A重合），连CP，作∠ACP和∠DCP的平分线分别交直线AB于点E、F.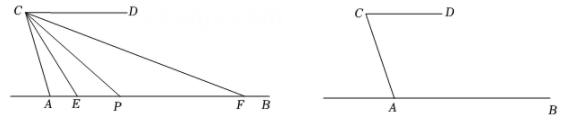
(1)、当点P在点A的右侧时；①若∠ACP＝36°，则此时CP是否平分∠ECF，请说明理由.
②求∠ECF的度数.
(2)、在点P运动过程中，直接写出∠APC与∠AFC之间的数量关系.23. 已知：四边形AOBC中，BC∥OA，OB⊥OA，D为射线OB上一动点，连接AD，DM∥ AC交直线BC于点M，作∠OAD的角平分线AN与 ∠BMD的角平分线MN所在直线交于点N．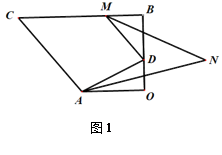
(1)、如图1，当D在线段OB上时，小芳将∠CAD和∠ANM的部分对应角度记录如下表：∠CAD
80°
90°
100°
110°
∠ANM
50°
45°
40°
25°
①请将上表补全；
②猜想∠CAD和∠ANM的数量关系，并说明理由．
(2)、当D点在OB延长线上运动时，在图2和图3中补全图形；并在各图下方横线上分别写出∠CAD和∠ANM的数量关系．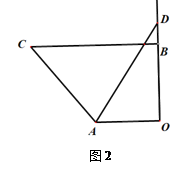
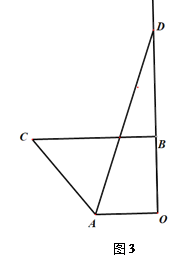24. 我区防汛指挥部在一河道的危险地带两岸各安置一探照灯，便于夜间查看江水及两岸河堤的情况．如图1，灯A光射线自AM顺时针旋转至AN便立即逆时针旋转至AM，如此循环.灯B光射线自BP顺时针旋转至BQ便立即逆时针旋转至BP，如此循环.两灯交叉照射且不间断巡视．若灯A转动的速度是a度/秒，灯B转动的速度是b度/秒，且a，b满足(a﹣4b)2+(a+b﹣5)2＝0．若这一带江水两岸河堤相互平行，即PQ∥MN，且∠BAN＝60°．根据相关信息，解答下列问题.
(1)、a= ， b=.(2)、若灯B的光射线先转动24秒，灯A的光射线才开始转动，在灯B的光射线到达BQ之前，灯A转动几秒，两灯的光射线互相平行？(3)、如图2，若两灯同时开始转动照射，在灯A的光射线到达AN之前，若两灯射出的光射线交于点C，过点C作CD⊥AC交PQ于点D，则在转动的过程中，∠BAC与∠BCD间的数量关系是否发生变化？若不变，请求出这两角间的数量关系；若改变，请求出各角的取值范围．25. 如图
(1)、如图1，点E在BC上，∠A＝∠D，∠ACB =∠CED．请说明 AB∥CD 的理由.(2)、如图2，AB∥CD，BG 平分∠ABE，与∠EDF 的平分线交于 H 点，若∠DEB比∠DHB 大60°，求∠DEB 的度数．(3)、保持（2）中所求的∠DEB 的度数不变，如图3，AB∥CD，BM 平分∠EBK，DN 平分∠CDE，作 BP∥DN，则∠PBM 的度数是否改变？若不变，请直接写出∠PBM 的度数；若改变，请说明理由．26. 光线反射是一种常见的物理现象，在生活中有广泛地应用.例如提词器可以帮助演讲者在看演讲词的同时也能面对摄像机，自行车尾部的反光镜等就是应用了光的反射原理.
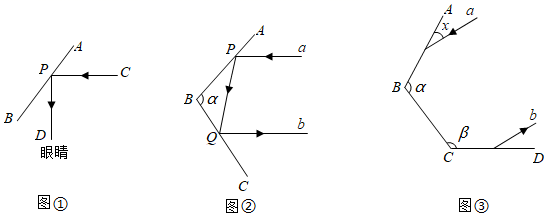(1)、提词器的原理如图①，AB表示平面镜，CP表示入射光线，PD表示反射光线，∠CPD＝90°，求∠APC的度数；(2)、自行车尾部的反光镜在车灯照射下，能把光线按原来的方向返回（如图②），a表示入射光线，b表示反射光线，a∥b.平面镜AB与BC的夹角∠ABC＝ ，求 .(3)、如图③，若 ＝108°，设平面镜CD与BC的夹角∠BCD＝ （90°＜ ＜180°），入射光线a与平面镜AB的夹角为x（0°＜x＜90°），已知入射光线a从平面镜AB开始反射，经过2或3次反射，当反射光线b与入射光线a平行时，请直接写出 的度数.（可用含x的代数式表示）.